Общие сведения. Погрешности прямых измеренийПогрешность измерений – это отклонение результата

Погрешности прямых измерений Погрешность измерений – это отклонение результата измерений от истинного значения измеряемой величины. По способу выражения различают абсолютную, относительную и приведенную погрешности измерения.

Абсолютная погрешность равна разности между результатом измерения и истинным значением измеряемой величины, выраженная в единицах измеряемой величины:

. (1.1)

Относительная погрешность d представляет собой отношение абсолютной погрешности измерения к истинному значению измеряемой величины, выраженное в процентах:

. (1.2)

Приведенная погрешность – это отношение абсолютной погрешности к нормирующему значению прибора, выраженное в процентах:

. (1.3)

Согласно ГОСТ 8.401-80 средствам измерений присваивают определённые классы точности. Классы точности выражаются одним числом, выражаемым из ряда 1·10ⁿ; 1,5·10ⁿ; 2·10ⁿ; 2,5·10ⁿ; 4·10ⁿ; 5·10ⁿ; 6·10ⁿ, где n = 1; 0; -1; -2 и т. д.

Классом точности средства измерения называется обобщенная его характеристика, определяемая пределами допускаемых основной погрешности и погрешностей, названных изменением значений влияющих величин.

Большинству аналоговых электроизмерительных приборов присваивается класс точности, определяемый основной наибольшей допустимой приведенной погрешностью

, (1.4)

где – предел допустимой максимальной абсолютной погрешности измерения.

У приборов, класс точности которых выражается одним числом, основная приведенная погрешность прибора в рабочем диапазоне рабочей шкалы, выраженная в процентах, не должна превышать значения, соответствующего класса точности.

Косвенные измерения. Это измерения, при которых искомое значение величины находят на основании известной зависимости между этой величиной и величинами , ,… , определяемыми прямыми измерениями, т. е.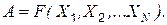

Очевидно, что абсолютная погрешность измеряемой величины является функцией абсолютных погрешностей прямых измерений:

.

В простейшем случае для одной переменной в результате измерения получим

.

Разложим правую часть в ряд Тейлора и сохраним члены разложения, содержащие в первой степени:

,

отсюда абсолютная погрешность равна

.

Относительная погрешность определяется выражением

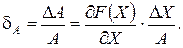
В общем случае для функции абсолютную погрешность результата косвенных изменений определяют выражением

относительную

.

Пример. Записать формулу для расчета абсолютной погрешности косвенного измерения мощности постоянного тока по показаниям амперметра I и вольтметра U.

Дата добавления: 2015-07-10