
|
Читайте также: |
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Для студентов 1 курса заочного обучения группы ИТСС, 2014 г.
Механика и молекулярная физика
Кинематика
Задача 1.5. Зависимость пройденного телом пути от времени задается уравнением  (м). Определить время после начала движения, через которое ускорение
(м). Определить время после начала движения, через которое ускорение  тела будет равно
тела будет равно  , а также среднюю скорость
, а также среднюю скорость  и среднее ускорение
и среднее ускорение  тела за этот промежуток времени.
тела за этот промежуток времени.
Задача 1.6. Автомобиль проехал первую половину пути со скоростью  , а вторую – со скоростью
, а вторую – со скоростью  . Определить среднюю скорость автомобиля на всем пройденном пути.
. Определить среднюю скорость автомобиля на всем пройденном пути.
Задача 1.7. Первую половину времени своего движения автомобиль перемещался со скоростью  , а вторую половину – со скоростью
, а вторую половину – со скоростью  . Найти среднюю скорость за все время движения автомобиля.
. Найти среднюю скорость за все время движения автомобиля.
Задача 1.8. Найти скорость  относительно берега лодки, идущей по течению, против течения и под углом
относительно берега лодки, идущей по течению, против течения и под углом 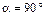 к направлению течения. Скорость течения реки
к направлению течения. Скорость течения реки  , скорость лодки относительно воды
, скорость лодки относительно воды  .
.
Задача 1.9. Лодка движется перпендикулярно к берегу со скоростью  . Течение относит ее вниз на расстояние
. Течение относит ее вниз на расстояние  . Найти скорость
. Найти скорость  течения реки и время
течения реки и время  , затраченное на переправу. Ширина реки
, затраченное на переправу. Ширина реки 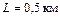 .
.
Задача 1.10. Лодка перемещается относительно воды в реке со скоростью  под углом
под углом  к течению, скорость которого
к течению, скорость которого  . Определить скорость
. Определить скорость  лодки относительно берега, ее направление по отношению к течению и перемещение к моменту времени
лодки относительно берега, ее направление по отношению к течению и перемещение к моменту времени  .
.
Задача 1.11. С аэростата, находящегося на высоте  , упал камень. Через какое время
, упал камень. Через какое время  камень достигнет Земли, если: а) аэростат поднимается со скоростью
камень достигнет Земли, если: а) аэростат поднимается со скоростью  ; б) аэростат опускается со скоростью
; б) аэростат опускается со скоростью  ; в) аэростат неподвижен.
; в) аэростат неподвижен.
Задача 1.12. Свободно падающее тело за последнюю секунду прошло  своего пути. Сколько времени и с какой высоты падало тело?
своего пути. Сколько времени и с какой высоты падало тело?
Задача 1.13. Небольшое тело брошено под углом  к горизонту с начальной скоростью
к горизонту с начальной скоростью  . Пренебрегая сопротивлением воздуха, найти дальность полета
. Пренебрегая сопротивлением воздуха, найти дальность полета  , наибольшую высоту подъема
, наибольшую высоту подъема 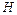 , время подъема до максимальной точки и время полета
, время подъема до максимальной точки и время полета  , уравнение траектории тела.
, уравнение траектории тела.
Задача 1.14. Чему равно отношение максимальных высот поднятия тел, брошенных под одним и тем же углом к горизонту с начальными скоростями  и
и 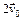 , над первоначальным уровнем?
, над первоначальным уровнем?
Задача 1.15. На высоте  горизонтально с постоянной скоростью летит самолет. С земли производится выстрел из орудия, причем скорость снаряда
горизонтально с постоянной скоростью летит самолет. С земли производится выстрел из орудия, причем скорость снаряда  в момент выстрела направлена на самолет под углом
в момент выстрела направлена на самолет под углом  к горизонту. С какой скоростью
к горизонту. С какой скоростью  летел самолет, если снаряд поразил цель?
летел самолет, если снаряд поразил цель?
Задача 1.16. Шарик падает с нулевой начальной скоростью на гладкую горизонтальную поверхность, образующую с горизонтом угол  . Пролетев расстояние
. Пролетев расстояние  , он упруго отскакивает от плоскости. Определить расстояние между точками первого и второго ударов.
, он упруго отскакивает от плоскости. Определить расстояние между точками первого и второго ударов.
Задача 1.17. Тяжелая горизонтальная плита движется вверх с постоянной скоростью  . Легкий шарик начинает свободно падать и, пролетев расстояние
. Легкий шарик начинает свободно падать и, пролетев расстояние  , сталкивается упруго с плитой. Определить время между двумя последовательными ударами шарика о плиту.
, сталкивается упруго с плитой. Определить время между двумя последовательными ударами шарика о плиту.
Задача 1.18. Каковы линейная и угловая скорости движения точек земной поверхности на широте Уфы ( ) при суточном вращении Земли? Радиус Земли 6400 км.
) при суточном вращении Земли? Радиус Земли 6400 км.
Задача 1.19. Твердое тело вращается вокруг неподвижной оси по закону  (рад). Найти: а) средние значения угловой скорости и углового ускорения за промежуток времени от
(рад). Найти: а) средние значения угловой скорости и углового ускорения за промежуток времени от  до остановки; б) угловое ускорение в момент остановки тела.
до остановки; б) угловое ускорение в момент остановки тела.
Задача 1.20. Диск радиусом 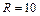 см вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением
см вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением  (рад). Определить для точек обода колеса к концу первой секунды после начала движения: а) угловую скорость
(рад). Определить для точек обода колеса к концу первой секунды после начала движения: а) угловую скорость  ; б) линейную скорость
; б) линейную скорость  ; в) тангенциальное
; в) тангенциальное  и нормальное
и нормальное 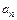 ускорение; г) полное ускорение
ускорение; г) полное ускорение  ; д) угол, составляемый вектором полного ускорения с радиусом колеса, проведенным через соответствующую точку обода.
; д) угол, составляемый вектором полного ускорения с радиусом колеса, проведенным через соответствующую точку обода.
 Задача 1.21. Колесо радиусом
Задача 1.21. Колесо радиусом 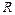 равномерно катится без скольжения по горизонтальному пути со скоростью
равномерно катится без скольжения по горизонтальному пути со скоростью  . Найти скорости точек 1, 2 и 3, выразив их через орты координатных осей. Найти также координаты
. Найти скорости точек 1, 2 и 3, выразив их через орты координатных осей. Найти также координаты 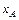 и
и  произвольной точки
произвольной точки  на ободе колеса как функции времени
на ободе колеса как функции времени  или угла поворота колеса
или угла поворота колеса  . В начальный момент
. В начальный момент 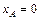 ,
, 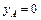 ,
,  . По найденным выражениям для
. По найденным выражениям для 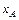 и
и  построить график траектории точки на ободе колеса.
построить график траектории точки на ободе колеса.
У к а з а н и е. Движение точек обода колеса можно рассматривать как результат сложения двух движений: поступательного движения со скоростью  оси колеса и вращения вокруг этой оси. Для этих точек при отсутствии скольжения колеса модули векторов скорости поступательного движения и линейной скорости, обусловленной вращением, равны друг другу.
оси колеса и вращения вокруг этой оси. Для этих точек при отсутствии скольжения колеса модули векторов скорости поступательного движения и линейной скорости, обусловленной вращением, равны друг другу.
Задача 1.22. Автомобиль с колесами радиусом 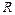 движется со скоростью
движется со скоростью  по горизонтальной дороге, причем
по горизонтальной дороге, причем  , где
, где 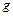 – ускорение свободного падения. На какую максимальную высоту
– ускорение свободного падения. На какую максимальную высоту  может быть заброшена вверх грязь, срывающаяся с колес автомобиля? Указать положение той точки на покрышке колеса, с которой при данной скорости движения автомобиля грязь будет забрасываться выше всего. Сопротивление воздуха движению отброшенного вверх грязи не учитывать.
может быть заброшена вверх грязь, срывающаяся с колес автомобиля? Указать положение той точки на покрышке колеса, с которой при данной скорости движения автомобиля грязь будет забрасываться выше всего. Сопротивление воздуха движению отброшенного вверх грязи не учитывать.
Задача 1.23. Якорь электродвигателя, вращавшийся с частотой 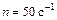 , после выключения тока двигаясь равнозамедленно, остановился, сделав полное число оборотов
, после выключения тока двигаясь равнозамедленно, остановился, сделав полное число оборотов  . Найти угловое ускорение якоря.
. Найти угловое ускорение якоря.
Дата добавления: 2015-07-12; просмотров: 86 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Методы их решения | | | ДИНАМИКА |