
Читайте также:
|
Лекция 3. Задача о назначениях. Задача коммивояжера.
В процессе управления производством возникают задачи назначения исполнителей на различные виды работ, например: подбор кадров и назначение кандидатов на вакантные должности, распределение источников капитальных вложении между различными проектами научно-технического развития, распределение экипажей самолетов между авиалиниями.
Задачу о назначениях можно сформулировать следующим образом. Необходимо выполнить N различных работ. Для их выполнения можно привлечь N рабочих. Каждый рабочий за определенную плату готов выполнить любую работу. Выполнение любой работы следует поручить одному рабочему. Любой рабочий может выполнить только одну работу. Требуется так распределить работы между рабочими, чтобы общие затраты на выполнение всех работ были минимальными.
Задача о назначениях в стандартной форме. При рассмотрении задачи о назначениях в стандартной форме предполагается, что количество рабочих равно количеству работ.
Обозначения:
сij — показатель эффективности назначения i -го рабочего на j -ую работу, например издержки выполнения i- м рабочим j -й работы;
xij — переменная модели (хij = 1, если i -й рабочий используется на j -й работе, и xij = 0 в противном случае).
Модель задачи о назначениях:
 (1)
(1)
 (2а)
(2а)
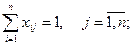 (2б)
(2б)
 (3)
(3)
Здесь (1) — целевая функция (минимум издержек на выполнение всех работ);
(2) — система ограничений, отражающая следующие условия:
а) каждая работа должна быть выполнена одним рабочим;
б) каждый рабочий может быть привлечен к одной работе;
(3) — условия двоичности переменных.
При решении задачи о назначениях исходной информацией является таблица задачи о назначениях с={ сij }, элементами которой служат показатели эффективности назначений. Для задачи о назначениях, записанной в стандартной форме, количество строк этой таблицы совпадает с количеством столбцов:

Результатом решения задачи о назначениях (1)—(3) является вектор х *={  }, компоненты которого — целые числа.
}, компоненты которого — целые числа.
Оптимальный план задачи о назначениях (1)—(3) можно представить в виде квадратной матрицы назначений, в каждой строке и в каждом столбце которой находится ровно одна единица. Такую матрицу иногда называют матрицей перестановок. Значение целевой функции (1), соответствующее оптимальному назначению, называют эффективностью назначений.
В комбинаторной интерпретации задача о назначениях заключается в определении такой перестановки исполнителей {1,2,…, n }, которая обеспечивает минимальную суммарную стоимость назначений. Очевидно, что решение такой задачи может быть получено перебором, однако существует ряд эффективных алгоритмов.
Введем необходимые определения.
Матрицей весов (или матрицей назначений) называется матрица вида C = {cij}n*n, где n – число вершин одной доли графа, в которой элементу cij присваивается значение веса соответствующего ребра двудольного графа.
Матрица C называется приведенной, если в каждом ее столбце и в каждой строке есть хотя бы один нуль.
Нулевые элементы матрицы C называются независимыми нулями, если для любого i, для которого выполняется условие 1<=i<=k, строка и столбец, на пересечении которых расположен элемент xi, не содержит другие нули xj для всех j 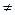 k.
k.
Для решения задачи о назначениях будем применять Венгерский алгоритм (алгоритм Куна) представленный в матричной форме.
Венгерский алгоритм (матричная форма)
В данном алгоритме происходит последовательное преобразование матрицы весов (назначений) для получения приведенной матрицы, в которой в каждом ее столбце и строке есть хотя бы один нуль. Решение будем искать на нулевых элементах (независимых нулях). Еще раз поясним, что нулевые элементы матрицы C называются независимыми нулями, если для любого i, для которого выполняется условие 1<=i<=k, строка и столбец, на пересечении которых расположен элемент xi, не содержит другие нули xj для всех j 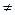 k
k
Следующая последовательность шагов описывает алгоритм решения задачи о назначениях венгерским методом:
Шаг 1. Среди элементов каждой строки матрицы весов выбрать минимальный и вычесть его из элементов этой строки.Повторить эту же процедуры для столбцов.Перейти к шагу 2.
Шаг 2. Попытаться сконструировать решение при помощи нулевых элементов. Для этого необходимо осуществить следующие действия: рассмотрим сначала ту строку (или те строки), которая содержит наименьшее число нулей; обведем квадратиком один из нулей этой строки и затем вычеркнем нули, которые находятся в той же строке и в том же столбце, что и обведенный нуль; найдем среди оставшихся строк ту (или те), которая содержит меньше всего нулей, и повторим тот же процесс. Будем так поступать до тех пор, пока станет невозможным обводить квадратиками новые нули. Если нельзя получить решение с независимыми нулями, то перейти к шагу 4, в противном случае останов: решение найдено.Перейти к шагу 3.
Шаг 3. Выполнить следующую последовательность действий:
а) пометить крестиком (x) все те строки, которые не содержат ни одного обведенного квадратиком нуля;
б) отметить каждый столбец, содержащий перечеркнутый нуль хотя бы в одной из помеченных строк;
в) отметим каждую строку, имеющую обведенный квадратиком нуль хотя бы в одном из помеченных столбцов;
г) будем повторять поочередно действия б) и в) до тех пор, пока не останется строк и столбцов, которые еще можно пометить.
В результате выполнения действий а) - г) будет получено минимальное число строк и столбцов, содержащих все перечеркнутые или обведенные нули таблицы.
Перейти к шагу 4.
Шаг 4. Перечеркнуть каждую непомеченную строку и каждый помеченный столбец, в результате чего получим минимальное число строк и столбцов, содержащих все перечеркнутые или обведенные нули таблицы.
Перейти к шагу 5.
Шаг 5. Рассмотрим часть таблицы, состоящую из неперечеркнутых элементов, и найдем минимальный элемент в ней. Вычесть это число из элементов неперечеркнутых столбцов и прибавить к элементам перечеркнутых строк. Результат данной процедуры записать в матрицу C2 и попробовать найти оптимальное решение на нулевых элементах. Если возможно получить оптимальное решение, то процесс заканчивается, иначе перейти к шагу 3.
Рассмотрим пример решения задачи о назначениях описанным методом с матрицей:
2 5 4 6 7 4
5 8 6 7 8 3
5 4 6 7 8 5
6 7 3 45 6 5
4 6 8 7 6 45
6 5 4 3 4 5
После вычитания минимального элемента из строк получится матрица:
0 3 2 4 5 2
2 5 3 4 5 0
1 0 2 3 4 1
3 4 0 42 3 2
0 2 4 3 2 41
3 2 1 0 1 2
После вычитания минимального элемента из столбцов получится приведенная матрица, которая будет иметь вид:
0 3 2 4 4 2
2 5 3 4 4 0
1 0 2 3 3 1
3 4 0 42 2 2
0 2 4 3 1 41
3 2 1 0 0 2
Обводим квадратиком (выделяем жирным шрифтом) нули:
0 3 2 4 4 2
2 5 3 4 4 0
1 0 2 3 3 1
3 4 0 42 2 2
0 2 4 3 1 41
3 2 1 0 0 2
Видим, что нет независимого элемента в 5 строке
Расставляем пометки: крестиком пометим строку 5, пометим столбец 1, пометим строку 1. Пометки расставлялись в соответствии с пунктами а), б), в) шага 3.
Непомеченными будут столбцы 2, 3, 4, 5, 6. Зачеркиваем столбец 1. Также зачеркнем все непомеченные строки.
Рассмотрим часть таблицы, состоящую из неперечеркнутых элементов. Минимальный элемент в ней 1. Вычитаем его из всех неперечеркнутых элементов.
После приведения матрица принимает вид:
0 2 1 3 3 1
2 5 3 4 4 0
1 0 2 3 3 1
3 4 0 42 2 2
0 1 3 2 0 40
3 2 1 0 0 2
Снова обводим квадратиками (выделяем жирным шрифтом) нули. Мы получили 6 независимых нулей. Следовательно, останов. Подсчитываем суммарный вес назначения, суммируя значения из исходной матрицы, стоящие на позициях независимых нулей
Вес равен 2+4+3+3+6+3 = 21.
В паросочетание входят ребра: 1,1; 3,2; 4,3; 6,4; 5,5; 2,6
Таким образом, получен результат (матрица назначений)
1 0 0 0 0 0
0 0 0 0 0 1
0 1 0 0 0 0
0 0 1 0 0 0
0 0 0 0 0 0
0 0 0 1 0 0
Задача коммивояжера
Имеется N городов, которые должен обойти коммивояжер с минимальными затратами. При этом на его маршрут накладывается два ограничения:
· маршрут должен быть замкнутым, то есть коммивояжер должен вернуться в тот город, из которого он начал движение;
· в каждом из городов коммивояжер должен побывать точно один раз, то есть надо обязательно обойти все города, при этом не побывав ни в одном городе дважды.
Для расчета затрат существует матрица условий, содержащая затраты на переход из каждого города в каждый, при этом считается, что можно перейти из любого города в любой, кроме того же самого (в матрице диагональ заполнена нулями, такие переходы коммивояжера запрещены). Целью решения является нахождения маршрута, удовлетворяющего всем условиям и при этом имеющего минимальную сумму затрат.
Задача коммивояжера может быть сформулирована как целочисленная введением булевых переменных  , если маршрут включает переезд из города i непосредственно в город j и
, если маршрут включает переезд из города i непосредственно в город j и  в противном случае. Тогда можно задать математическую модель задачи, то есть записать целевую функцию и систему ограничений:
в противном случае. Тогда можно задать математическую модель задачи, то есть записать целевую функцию и систему ограничений:
 (4)
(4)

Условия (5) – (7) в совокупности обеспечивают, что каждая переменная  равна или нулю, или единице. При этом ограничения (5), (6) выражают условия, что коммивояжер побывает в каждом городе один раз в него прибыв (ограничение (5)), и один раз из него выехав (ограничение (6)).
равна или нулю, или единице. При этом ограничения (5), (6) выражают условия, что коммивояжер побывает в каждом городе один раз в него прибыв (ограничение (5)), и один раз из него выехав (ограничение (6)).
Однако этих ограничений не достаточно для постановки задачи коммивояжера, так как они не исключают решения, где вместо простого цикла, проходящего через n вершин, отыскиваются 2 и более отдельных цикла (подцикла), проходящего через меньшее число вершин. Поэтому задача, описанная уравнениями (5)–(7) должна быть дополнена ограничениями, обеспечивающими связность искомого цикла.
Для того, чтобы исключить при постановке задачи все возможные подциклы в систему ограничений задачи включают следующее ограничение:  , где
, где  ,
,  и
и  .
.
Ограничения (5)-(7) соответствуют ограничениям задачи о назначениях, которая отличается от задачи коммивояжера отсутствием требования цикличности пути.
Задача коммивояжера в математической постановке эквивалентна задаче упорядочения конечного числа работ на машине при учете потерь от переналадок. Во многих случаях длительность переналадок машины перед выполнением некоторой работы нельзя считать не зависящей от характера предшествующей работы. Иногда разброс длительностей переналадок становится основным критерием оценки расписания. Хорошей иллюстрацией задачи упорядочения с учетом издержек от переналадок является производство красок. Краски различного цвета можно получить на одном и том же оборудовании, которое должно очищаться при каждой перемене цвета изготовляемой краски. Суммарная длительность очистки сильно зависит от последовательности перехода от одного цвета краски к другому. Возникает задача нахождения такой последовательности, в которой суммарные потери от переналадок минимальны. Для задачи упорядочения каждая работа соответствует городу, а длительность переналадки – расстоянию между городами.
Матрица С, вообще говоря, может быть несимметричной, так как затраты. связанные с переналадкой с i -ой работы на j -ю, как правило отличны от затрат при переходе от j -ой работы к i -ой.
Существует несколько точных метолов решения задачи коммивояжера: метод ветвей и границ, динамическое программирование и другие. Методов ветвей и границ с использованием ЭВМ можно решать задачи коммивояжера для n £40, динамического программирования – для n £17.
В связи с такой малой эффективностью точных методов получили широкое применение эвристические. В настоящее время существует более ста приближенных методов решения задачи коммивояжера, среди которых наиболее прост метод ближайшего соседа. Он реализует требование включать в искомый замкнутый маршрут город, ближайший к только что найденному. Алгоритм «ближайшего соседа» состоит в последовательном добавлении к начальному городу следующего ближайшего к нему и так далее. Метод очень прост, однако степень приближения к оптимальному решению сильно зависит от выбора начального города. Поэтому алгоритм целесообразно применять, начиная с каждого города, и затем выбрать замкнутый маршрут наименьшей длины.
На обширном статистическом материале оказано, что с увеличением числа городов n ошибка решения убывает. Поэтому при n £40 можно применять точные методы, а при n >40 - приближенные типа «ближайшего соседа».
Рассмотрим алгоритм решения задачи коммивояжера методом ветвей и границ.
Для практической реализации идеи метода ветвей и границ применительно к задаче коммивояжера нужно найти метод определения нижних границ подмножества и разбиения множества гамильтоновых контуров на подмножества (ветвление).
Определение нижних границ базируется на том утверждении, что если ко всем элементам i -й строки или j -го столбца матрицы C прибавить или отнять число  , то задача останется эквивалентной прежней, то есть оптимальность маршрута коммивояжера не изменится, а длина любого гамильтонова контура изменится на данную величину
, то задача останется эквивалентной прежней, то есть оптимальность маршрута коммивояжера не изменится, а длина любого гамильтонова контура изменится на данную величину  .
.
Опишем алгоритм Литтла для нахождения минимального гамильтонова контура для графа с n вершинами. Граф представляют в виде матрицы его дуг. Если между вершинами Xi и Xj нет дуги, то ставится символ «∞».
Алгоритм Литтла для решения задачи коммивояжера можно сформулировать в виде следующих правил:
1. Находим в каждой строке матрицы  минимальный элемент
минимальный элемент  и вычитаем его из всех элементов соответствующей строки. Получим матрицу, приведенную по строкам, с элементами
и вычитаем его из всех элементов соответствующей строки. Получим матрицу, приведенную по строкам, с элементами
 .
.
2. Если в матрице  , приведенной по строкам, окажутся столбцы, не содержащие нуля, то приводим ее по столбцам. Для этого в каждом столбце матрицы
, приведенной по строкам, окажутся столбцы, не содержащие нуля, то приводим ее по столбцам. Для этого в каждом столбце матрицы  выбираем минимальный элемент
выбираем минимальный элемент 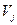 ,
,  и вычитаем его из всех элементов соответствующего столбца. Получим матрицу
и вычитаем его из всех элементов соответствующего столбца. Получим матрицу
 ,
,
каждая строка и столбец, которой содержит хотя бы один нуль. Такая матрица называется приведенной по строкам и столбцам.
3. Суммируем элементы  и
и 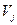 , получим константу приведения
, получим константу приведения
 ,
,
которая будет нижней границей множества всех допустимых гамильтоновых контуров, то есть
 .
.
4. Находим степени нулей для приведенной по строкам и столбцам матрицы. Для этого мысленно нули в матице заменяем на знак «∞» и находим сумму минимальных элементов строки и столбца, соответствующих этому нулю. Записываем ее в правом верхнем углу клетки:
 .
.
5. Выбираем дугу  , для которой степень нулевого элемента достигает максимального значения
, для которой степень нулевого элемента достигает максимального значения
 .
.
6. Разбиваем множество всех гамильтоновых контуров  на два подмножества
на два подмножества  и
и  . Подмножество
. Подмножество  гамильтоновых контуров содержит дугу
гамильтоновых контуров содержит дугу  ,
,  - ее не содержит. Для получения матрицы контуров
- ее не содержит. Для получения матрицы контуров  , включающих дугу
, включающих дугу  , вычеркиваем в матрице
, вычеркиваем в матрице  строку
строку  и столбец
и столбец  . Чтобы не допустить образования негамильтонова контура, заменим симметричный элемент
. Чтобы не допустить образования негамильтонова контура, заменим симметричный элемент  на знак «∞».
на знак «∞».
7. Приводим матрицу гамильтоновых контуров  . Пусть
. Пусть  - константа ее приведения. Тогда нижняя граница множества
- константа ее приведения. Тогда нижняя граница множества  определится так:
определится так:
 .
.
8. Находим множество гамильтоновых контуров  , не включающих дугу
, не включающих дугу  . Исключение дуги
. Исключение дуги  достигается заменой элемента
достигается заменой элемента  в матрице
в матрице  на ∞.
на ∞.
9. Делаем приведение матрицы гамильтоновых контуров  . Пусть
. Пусть  - константа ее приведения. Нижняя граница множества
- константа ее приведения. Нижняя граница множества  определится так:
определится так:
 .
.
10. Сравниваем нижние границы подмножества гамильтоновых контуров  и
и  . Если
. Если  , то дальнейшему ветвлению в первую очередь подлежит множество
, то дальнейшему ветвлению в первую очередь подлежит множество  . Если же
. Если же  , то разбиению подлежит множество
, то разбиению подлежит множество  .
.
Процесс разбиения множеств на подмножества сопровождается построением дерева ветвлений.
11. Если в результате ветвлений получаем матрицу  , то определяем полученный ветвлением гамильтонов контур и его длину.
, то определяем полученный ветвлением гамильтонов контур и его длину.
12. Сравниваем длину гамильтонова контура с нижними границами оборванных ветвей. Если длина контура не превышает их нижних границ, то задача решена. В противном случае развиваем ветви подмножеств с нижней границей, меньшей полученного контура, до тех пор, пока не получим маршрут с меньшей длиной или не убедимся, что такого не существует.
Рассмотрим пример реализации алгоритма, для матрицы расстояний, представленной в таблице 1. Необходимо с помощью алгоритма Литтла решить задачу коммивояжера.
Табл.1
| j i | ||||||
| ∞ | ||||||
| ∞ | ||||||
| ∞ | ||||||
| ∞ | ||||||
| ∞ | ||||||
| ∞ |
1) Справа к таблице присоединяем столбец Ui, в котором записываем минимальные элементы соответствующих строк. Вычитаем элементы Ui из соответствующих элементов строки матрицы.
| j i | Ui | ||||||
| ∞ | |||||||
| ∞ | |||||||
| ∞ | |||||||
| ∞ | |||||||
| ∞ | |||||||
| ∞ |
2) Внизу полученной матрицы присоединяем строку Vj, в которой записываем минимальные элементы столбцов. Вычитаем элементы Vj из соответствующих столбцов матрицы.
| j i | ||||||
| ∞ | ||||||
| ∞ | ||||||
| ∞ | ||||||
| ∞ | ||||||
| ∞ | ||||||
| ∞ | ||||||
| Vj |
3) В результате вычислений получаем матрицу, приведенную по строкам и столбцам, которая изображена в виде таблицы 2.
Табл.2
| j i | ||||||
| ∞ | 019 | |||||
| 03 | ∞ | 02 | ||||
| 04 | ∞ | |||||
| 00 | ∞ | 04 | ||||
| 07 | ∞ | |||||
| 010 | ∞ |
4) Находим константу приведения:
 .
.
Таким образом, нижней границей множества всех гамильтоновых контуров будет число  .
.
5) Находим степени нулей полностью приведенной матрицы. Для этого как бы заменяем в ней все нули на знак «∞» и устанавливаем сумму минимальных элементов соответствующей строки и столбца. Степени нулей записаны в правых верхних углах клеток, для которых  .
.
6) Определяем максимальную степень нуля. Она равна 19 и соответствует клетке (1;5). Таким образом, претендентом на включение в гамильтонов контур является дуга (1;5).
7) Разбиваем множество всех гамильтоновых контуров  на два:
на два:  и
и  . Матрицу
. Матрицу  с дугой (1;5) получаем табл.2 путем вычеркивания строки 1 и столбца 5. Чтобы не допускать образования негамильтонова контура, заменяем элемент (5;1) на знак «∞».
с дугой (1;5) получаем табл.2 путем вычеркивания строки 1 и столбца 5. Чтобы не допускать образования негамильтонова контура, заменяем элемент (5;1) на знак «∞».
| j i | |||||
| 0 | ∞ | 0 | |||
| 0 | ∞ | ||||
| 0 | ∞ | 0 | |||
| ∞ | 0 | ||||
| 0 | ∞ |
8) Матрицу гамильтоновых контуров  получим из таблицы 2 путем замены элемента (1;5) на знак «∞».
получим из таблицы 2 путем замены элемента (1;5) на знак «∞».
| j i | |||||||
| ∞ | ∞ | ||||||
| 0 | ∞ | 0 | |||||
| 0 | ∞ | ||||||
| 0 | ∞ | 0 | |||||
| 0 | ∞ | ||||||
| 0 | ∞ | ||||||
9) Делаем дополнительное приведение матрицы контуров  :
:  = 0. Нижняя граница множества
= 0. Нижняя граница множества  равна
равна  .
.
10) Находим константу приведения для множества контуров  :
:  . Следовательно, нижняя граница множества
. Следовательно, нижняя граница множества  равна
равна  .
.
11) Сравниваем нижние границы подмножеств  и
и  . Так как
. Так как  , то дальнейшему ветвлению подвергаем множество
, то дальнейшему ветвлению подвергаем множество  .
.
На рис.1 представлено ветвление по дуге (1;5).

рис.1
Переходим к ветвлению подмножества  . Его приведенная матрица представлена в таблице ниже.
. Его приведенная матрица представлена в таблице ниже.
| j i | |||||
| 03 | ∞ | 02 | |||
| 04 | ∞ | ||||
| 00 | ∞ | 04 | |||
| ∞ | 010 | ||||
| 010 | ∞ |
12) Узнаем степени нулей матрицы. Претендентами на включение в гамильтонов контур будут несколько дуг (5;2) и (6;3). Для дальнейших расчетов выберем дугу (6;3). Разбиваем множество  на два подмножества:
на два подмножества:  и
и  (табл. 3 и 4). Чтобы не допустить образования негамильтонова контура, в таблице 3 заменяем элемент (3;6) на знак «∞»
(табл. 3 и 4). Чтобы не допустить образования негамильтонова контура, в таблице 3 заменяем элемент (3;6) на знак «∞»
Табл.3
| j i | ||||
| 0 | ∞ | 0 | ||
| ∞ | ||||
| ∞ | 0 | |||
| ∞ | 0 |
Табл.4
| j i | ||||||
| 0 | ∞ | 0 | ||||
| 0 | ∞ | |||||
| 0 | ∞ | 0 | ||||
| ∞ | 0 | |||||
| ∞ | ∞ | |||||
Определим константы приведения для этих матриц  ,
,  . Следовательно,
. Следовательно,  ,
,  . Так как
. Так как  , то дальнейшему ветвлению подлежит подмножество
, то дальнейшему ветвлению подлежит подмножество  . Находим степени нулей матрицы.
. Находим степени нулей матрицы.
| j i | ||||
| 03 | ∞ | 02 | ||
| 022 | ∞ | |||
| 00 | ∞ | 08 | ||
| ∞ | 010 |
Претендентом к включению в гамильтонов контур станет дуга (3;2). Разбиваем множество  на два
на два  и
и  .
.
| j i | ||||
| 0 | 8 | |||
| ∞ | ||||
| ∞ | 10 |
| j i | |||||
| 0 | ∞ | 0 | |||
| ∞ | ∞ | ||||
| ∞ | 0 | ||||
| ∞ | 0 |
Очевидно,  ,
,  . Следовательно, очередному ветвлению нужно подвергнуть подмножество
. Следовательно, очередному ветвлению нужно подвергнуть подмножество  .
.
Переходим к ветвлению подмножества  . Его приведенная матрица представлена в таблице ниже.
. Его приведенная матрица представлена в таблице ниже.
| j i | |||
| 03 | 00 | 8 | |
| ∞ | 011 | ||
| ∞ | 037 |
Определяем степени нулей. Претендентом на включение в гамильтонов контур является дуга (5;4). Разбиваем множество  на два подмножества:
на два подмножества:  и
и  .
.
| j i | ||
| 0 | ||
| j i | ||||
| 0 | 0 | 8 | ||
| ∞ | 0 | |||
| ∞ | ∞ |
Находим нижние границы  ,
,  . Следовательно, очередному ветвлению нужно подвергнуть подмножество
. Следовательно, очередному ветвлению нужно подвергнуть подмножество  . Но его матрица имеет размерность
. Но его матрица имеет размерность  . Поэтому в гамильтонов контур следует включить дуги, соответствующие в матрице
. Поэтому в гамильтонов контур следует включить дуги, соответствующие в матрице  нулевым элементам. Это дуги (2;1) и (4;6).
нулевым элементам. Это дуги (2;1) и (4;6).
На рис.2 представлено дерево ветвлений. Определим полученный гамильтонов контур. В него вошли дуги  . Длина контура равна
. Длина контура равна  . Так как границы оборванных ветвей больше длины контура 1 – 5 – 4 – 6 – 3 – 2 – 1, то этот контура имеет наименьшую длину.
. Так как границы оборванных ветвей больше длины контура 1 – 5 – 4 – 6 – 3 – 2 – 1, то этот контура имеет наименьшую длину.

рис.2
Резюме
Задача о назначениях и задача коммивояжера являются задачами целочисленного линейного программирования, в которых переменные могут принимать не любые целые значения, а только значения 0 – ответ «нет» и 1 – ответ «да». Такие переменные называют логическими или булевыми. Решением задачи о назначениях является перестановка, обеспечивающая оптимальное значение целевой функции. Целевая функция минимизирует суммарные затраты, связанные с назначениями.
В задаче коммивояжера требуется найти оптимальную последовательность обхода городов, не допускающую подциклов в решении. Задача коммивояжера относится к классу неполиномиально сложных, или комбинаторных задач. Точное решение задачи может быть найдено только перебором вариантов. Метод ветвей и границ позволяет оценить решения, содержащиеся в некоторых подмножествах вариантов и выбрагь для развития такое подмножество, для которого оценка вариантов наилучшая. Отбрасывание вариантов осуществляется по сравнению оценок или по достижению предельного или приемлемого решения.
Дата добавления: 2015-07-12; просмотров: 85 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Пример решения задачи о назначениях в Excel | | | Кинематика |