Секторные токопроводящие жилы

Выведем формулу для площади секторной токопроводящей жилы. На рис. 1.15 представлен чертеж секторной жилы.

Рис. 1.15. Секторная жила

Введем некоторые обозначения: b – ширина сектора; h – высота сектора; D_из – толщина изоляции; R – радиус сектора; r – радиус закругления; 2b – угол 2p/3; 2g – рассчитываемый угол; S – площадь сектора.

Для удобства вычисления площади сектора S, разобьем его на элементарные площади: S ₁, S ₂, S ₃, S ₄, S ₅, S ₆, S ₇, S ₈, S ₉ (рис. 1.16). Площадь сектора S = S ₁ + S ₂ + S ₃ + S ₄, где S ₁ – площадь сегмента ABC; S ₂ – площадь прямоугольника QMNH; S ₃ – площадь треугольника QHF за вычетом площадей S ₇ + S ₉; S ₄ – площадь окружности радиусом r за вычетом площади сектора S ₅, которая является суммой площадей фигуры AMM ₁ и фигуры BNN ₁ . Площадь сегмента S ₁ (ABC) равна разности площадей сектора OACB и треугольника OAB (см. рис. 1.15):

(1.45)

Рассмотрим отдельно треугольник OAB, выразим его площадь через известные компоненты:

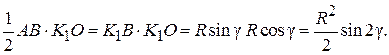(1.46)

Таким образом, площадь

(1.47)

Рис. 1.16. Разбиение сектора на элементарные площади

Площадь прямоугольника QMNH

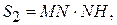
где и .

Из треугольника O ₂ NB находим NO ₂ = r cos g, , тогда площадь

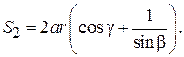(1.48)

Найдем площадь фигуры QHELG:

(1.49)

где площадь треугольника 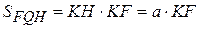. Из отношения выразим KF: , тогда площадь

(1.50)

Для нахождения площади S ₄ необходимо из площади круга с радиусом r вычесть площадь сегмента S ₅ и добавить S ₆ и S ₈:

S ₄ = p r ² – S ₅ + S ₆ + S ₈, (1.51)

где = + .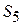

Площадь S ₅ – площадь сегмента, который подобен сегменту ABC, следовательно:

(1.52)

Общая площадь секторной токопроводящей жилы(S = S ₁ + S ₂ + S ₃ + S ₄)

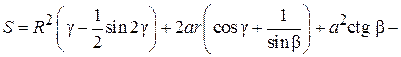
Учитывая, что S ₆ = S ₇ и S ₈ = S ₉, получим

(1.53)

В треугольнике OWO ₂ (см. рис. 1.15) сторона OO ₂ равна R – r, следовательно:

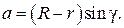(1.54)

Ширина сектора

(1.55)

Из треугольника OO ₂ D ₁имеем

(1.56)

откуда

(1.57)

Высота сектора h:

CL = OC – OO ₃ + O ₃ L,

где OC = R, O ₃ L = r.

Принимая во внимание, что OO ₃ = O ₂ H ₂ и O ₂ D ₁ = r + D_из, из треугольника O ₂ H ₂ D ₁ найдем:

O ₂ H ₂ = OO ₃ = (r + D_из)/sinb.

Окончательно имеем

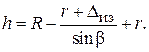(1.58)

Порядок расчета секторной жилы:

1. Задаем площадь поперечного сечения токопроводящей жилы S, радиус закругления сектора r и толщину изоляции D_из.

2. Задаем приближенное значение .

3. Вычисляем угол g по формуле (1.57).

4. Определяем a по формуле (1.54).

5. Вычисляем сечение S _р по формуле (1.53). Сравниваем рассчитанное значение S _рс заданным S. В том случае, если рассчитанное значение S _рменьше заданного S, произвольно увеличиваем R на некоторую небольшую величину и повторяем расчет с пункта 3 до тех пор, пока S _р не будет равно S с наперед заданной точностью.

6. Вычисляем высоту h и ширину b сектора.

Дата добавления: 2015-07-12