Конструкции токопроводящих жил

Рассмотрим пять конструкций токопроводящих жил, скрученных нормальной правильной скруткой, которые отличаются друг от друга числом проволок в центре жилы.

1. Одна проволока в центре (рис. 1.10).

Система скрутки 1 + 6 + 12 + 18 +… Диаметр первого повива – d, второго – 3 d, третьего – 5 d и т.д., такой ряд соответствует формуле для диаметра жилы

(1.23)

где n – число повивов; d – диаметр проволоки.

Определим общее число проволок, используя формулы арифметической прогрессии:

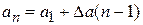, (1.24)

Рис. 1.10. Одна прово- лока в центре

где N – общее число проволок; a ₁ – первый член прогрессии; a_n – последний член прогрессии; D a – разность прогрессии; n – число членов прогрессии.

Для системы скрутки 1 + 6 + 12 + 18 +… применить формулы арифметической прогрессии можно только начиная со второго повива, так как первый повив отличается от второго на 5 проволок (это исключение из правила). В последнем повиве число проволок

, (1.25)

где первая шестерка – число проволок во втором повиве; вторая шестерка – число проволок, на которое увеличивается их количество в каждом следующем повиве; вторая единица указывает на то, что счет идет со второго повива.

Общее число проволок в жиле

. (1.26)

Эта формула получена без учета центральной проволоки. Запишем эту формулу с учетом центральной проволоки:

. (1.27)

Используя формулы (1.2), (1.23) и (1.27), найдем коэффициент заполнения жилы:

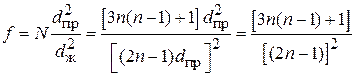. (1.28)

2. Две проволоки в центре (рис. 1.11).

Система скрутки 2 + 8 + 14 +… Диаметр жилы

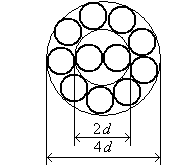
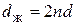. (1.29)

В последнем повиве число проволок

.

Общее число проволок в жиле

Рис. 1.11. Две прово- локи в центре

. (1.30)

Используя формулы (1.2), (1.29) и (1.30), найдем коэффициент заполнения:

. (1.31)

3. Три проволоки в центре (рис. 1. 12).

Рис. 1.12. Три проволоки в центре

Система скрутки 3 + 9 + 15 +…

Общее число проволок

. (1.32)

Рассмотрим D ABC:

. (1.33)

Из (1.33) выразим BC:

. (1.34)

Диаметр первого повива (см. рис. 1.13)

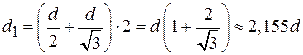. (1.35)

Диаметр жилы

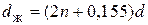. (1.36)

Используя формулы (1.2), (1.32) и (1.36), найдем коэффициент заполнения жилы:

. (1.37)

4. Четыре проволоки в центре (рис. 1.13).

Система скрутки 4 + 10 + 16 +…

В квадрате ABCD сторона BD = , диаметр первого повива . Тогда диаметр жилы

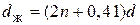. (1.38)

Рис. 1.13. Четыре проволоки в центре

Число проволок в жиле

. (1.39)

Используя формулы (1.2), (1.38) и (1.39), найдем коэффициент заполнения жилы:

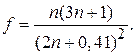(1.40)

5. Пять проволок в центре жилы (рис. 1.14).

Система скрутки 5 + 11 + 17 +…

Рассмотрим пятиугольник ABCDE, диаметр окружности, описывающей этот пятиугольник,

Диаметр первого повива

(1.41)

Диаметр жилы

. (1.42)

Рис. 1.14. Пять проволок в центре

Число проволок в жиле

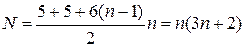. (1.43)

Используя формулы (1.2), (1.42) и (1.43), найдем коэффициент заполнения жилы:

. (1.44)

Жила с пятью проволоками в центре применяется редко из-за неустойчивости. Наиболее устойчива жила с одной проволокой в центре.

Дата добавления: 2015-07-12