Порядок формирования оценок по дисциплине

Для успешного обучения и сдачи зачетной работы слушателям ПО предлагается домашняя работа, в которой выделены три основные раздела: математический анализ, дифференциальные уравнения и линейная алгебра. Ниже приведены некоторые варианты домашних работ и вариант зачетной работы за первое полугодие.

8.1-Домашнее задание по функциям многих переменных:

1 Пусть .

1.1 (1) Вычислить градиент в точке .

1.2 (1) Вычислить производную по направлению, указывающему из точки в точку .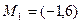

1.3 (1) Написать уравнение плоскости, касательной к поверхности в точке .

2 (4) Пусть 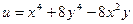. Найти все возможные точки локального экстремума и определить типы экстремумов. (за точку (0, 0) – премия 2 очка)

3 (4) Пусть . Функция 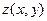задана неявно уравнением . Найти какой-либо экстремум этой функции, определить тип экстремума.

4 Дана система .

4.1 (3) Графически найти все точки условного экстремума функции при условии (2), определить их тип.

4.2 (3) Провести это же исследование методом множителей Лагранжа.

5 (6)

Методом множителей Лагранжа найти экстремумы функции при

условии: .

8.2 Домашнее задание по функциям одной переменной

1.Найти производные высоких порядков функций

1.1 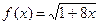3-го порядка в точке ; 1.2 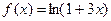19-го порядка в точке . 1.3 7-го порядка в точке . 1.4 17-го порядка в точке х=1. 1.5 23-го порядка в точке х=1

2. Найти первый и второй дифференциалы функцй в заданной точке

2.1. 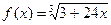в точке . 2.2 в точке х=1.

2.3 Функций, заданных неявно уравнением: 2.3.1 в точке (1,1)

отв.(?) 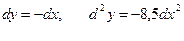2.3.2. в точке (1;2)

отв.(?) 2.4. Функций у=f(x), заданных параметрически системой уравнений: 2.4.1. в точке.

2.4.2. в точке. 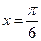2.4.3. 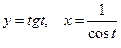в точке .

3. Найти экстремумы функций y=f(x), заданных неявно уравнением:

3.1 . 3.2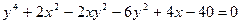

3.3. .

4. Доказать, что , используя определение предела функции в точке.

5. Доказать, что 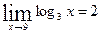, используя определение предела функции в точке.

6. Доказать, что , используя определение предела функции в точке.

7.Найти такое значение параметра «а», при котором предел 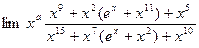при равен числу не равному нулю.

8..Найти уравнение наклонной асимптоты графика функции

8.1 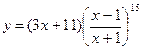. 8.2 . 8.3 . 8.4 ..9.Найти экстремумы функций и указать тип (максимум-минимум):

9.1 «плюс» найти наибольшую абсциссу точки перегиба.

9.2 «плюс» найти наибольшую абсциссу точки перегиба.

8.3 Домашнее задание по функциям одной переменной (вариант2)

1 ; 5.2 ; 5.3 .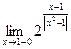

6. Вывести с помощью определения производную функции .

7. Найти функцию вида эквивалентную данной

при .

8. Найти производные функций: 8.1 ; 8.2 ;

8.3. Ф-ции , заданной неявно уравнением в точке (1;1);

8.4 Функции , заданной параметрически системой уравнений .

9.Найти уравнение наклонной асимптоты графика функции .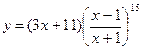

10. Найти все значения параметра «а», при которых

из неравенства (1): следует неравенство (2): .

11. Найти первый и второй дифференциалы функции .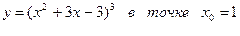

12. Исследовать функцию и построить эскиз её графика. Найти уравнение касательной проведенной в точке перегиба графика этой функции..

8.4 Домашнее задание по дифференциальным уравнениям.

1.

1.1 Решить задачу Коши: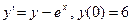

1.2 Построить график решения.

2. Решить одну из следующих задач:

2.1 Найти решение уравнения , удовлетворяющее условию . После этого найти .

2.2 Решить задачу Коши:

Найти значение

2.3 Решить уравнение: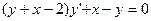

2.4 Решить уравнение:

2.5 Решить задачу Коши: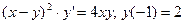

3. Решить одну из следующих задач:

3.1 Найти мнимую часть числа:

3.2 Решить задачу Коши: . После этого найти .

4. Решить систему уравнений

5. Решить одну из следующих задач:

5.1 Решите неоднородную систему и изобразите фазовый портрет однородной системы, соответствующей данной.

5.2 Найдите положение равновесия системы ;

- определить характер устойчивости хотя бы одной точки равновесия, рассмотрев линеаризованную систему;

- изобразить фазовый портрет линеаризованной системы.

6. Дано уравнение: .

6а) Не решая уравнения, указать на плоскости X0Y области возрастания/убывания интегральных кривых;

6б) Не решая уравнения, указать на том же чертеже области выпуклости вниз/вверх;

6в) Нарисовать три-четыре интегральных кривых.

7. Решить одну из следующих задач:

7.1 Решить уравнение: . Подсказка ;

7.2 Решить задачу Коши:

7.3 Решить уравнение:

7.4 Решить уравнение: ;

7.5 Решить задачу Коши: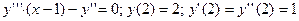

8. Указать решения соответствующего однородного уравнения и структуру частного решения , соответствующего правой части данных ДУ:

8.1 ; 8.2

8.3 ; 8.4

9. Пару кроликов откармливали и через два месяца они начали размножаться по такому закону: каждая пара зрелых кроликов стала приносить две новых пары, причем новорожденные становятся зрелыми через один месяц после рождения. Если - число пар кроликов через k месяцев, то:

9.1 Составить разностное уравнение на ;

9.2 Решить это уравнение и найти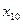

10. Найти уравнение линии, у которой отрезок касательной, заключенный между осями координат, делится пополам точкой касания.

8.5 Проект итоговой зачетной работы

1. Для графика функции найти уравнение

касательной (5 баллов) в точке .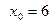

2.Найти производные функций

2.1 (5 баллов) в точке ;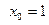

2.2 (7 баллов) в точке.

2.3 (10 баллов) в точке .

3. Решить методом Гаусса (сведением к треугольному виду) систему уравнений:

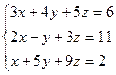
4. Является ли второй дифференциал 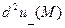в некоторой точке М равный

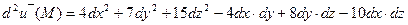положительно определенным? Дать объяснения.

5.Найти пределы

5.1. 5.2. 5.3.

6. Решить систему уравнений АХ=В, где А= В= матричным методом.

7. Найти уравнение наклонной асимптоты графика функции

8. Найти первый (5 баллов) и второй (10 баллов) дифференциалы функции заданной неявно уравнением 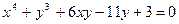в заданной точке (1;1)

9а. Изобразить на плоскости ХОУ линию , где

Изобразить несколько (3-4) линий уровня функции .

Качественно - по графику - обнаружить все точки локального экстремума функции «z» при условии

9в Методом множителей Лагранжа решить задачу поиска экстремума функции

при условии . Подтвердить решение качественным анализом.

10. Найти определитель матрицы А, где А=

11. Найти пределы функций

11.1. 11.2.

12. Решить любые два дифференциальных уравнения из предложенных ниже:

12.1. при условии. ..

12.2..

.12.3.. .

12.4.. при условии.

.

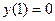
12.5.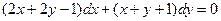

12.6...

12.7.. при условии. ..

13. Найти собственные векторы и собственные значения матрицы А=.

14. Решить дифференциальные уравнения:

14.1.. при условии .

14.2.

15. Найти все решения системы: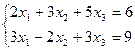

16. Решить систему Д.У. . Исследовать решение на устойчивость.

17. Найти , где матрица А=

18. Исследовать функцию . При каких «а» уравнение: имеет ровно три корня?

Результирующая оценка за промежуточный контроль в I семестре выставляется по следующей формуле

О_{итог_I} = 0,8·О_зачет + 0,2·О_{дз_I},

где О_зачет – оценка за зачетную работу, в 1 семестре, О_{дз_I} – оценка за домашнее задание в I семестре; при этом сумма 0,2·О_дз в результирующей оценке за промежуточный контроль составляет так называемую накопительную часть за работу в I семестре. Оценка за зачетную работу является блокирующей.

Дата добавления: 2015-07-12