СЛАЙД 18

Решив задачу поиска коэффициента фазового замедления, мы получаем набор дисперсионных зависимостей . Используя их для расчёта элементов матрицы, можно получить систему, имеющую не нулевые решения.

Элементы матриц и амплитудные коэффициенты представляют собой комплексные числа, для поиска решений системы вводится функционал следующего вида:

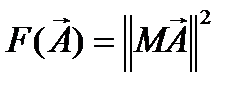
Чтобы обеспечить устойчивость функционал привязывается к решениям, найденным при других значениях параметров волновода. Например, сначала находится решение при толщине равной , теперь при вычислении функционала для толщины нужно, чтобы разница между новым решением и старым уменьшалась при уменьшении величины шага . Таким образом, функционал приводится к следующему виду:

Для минимизации данного функционала было использовано два алгоритма численной оптимизации: симплекс метод Нелдера-Мида и метод Хука-Дживса. Оба эти метода имеют нулевой порядок, т.е. при работе они опираются непосредственно на значения функции и вычисление производных не требуется. Данные алгоритмы предназначены для минимизации функций с действительными аргументами, поэтому для программной реализации двумерный вектор комплексных амплитуд заменялся соответствующим четырёхмерным вектором:

Дата добавления: 2015-07-12