Система 36 пар гексаграмм

В “Книге перемен” все 64 гексаграммы связаны в 32 пары, из которых в четырех парах (№ 1—2, 27—28, 29—30, 61—62) гексаграммы объединены по принципу “противоположности” (дуй), поскольку при переворачивании они обращаются сами в себя. Выше показывалось, что для календарных нужд две из этих пар (№ 27—28, 61—62) возможно развернуть в четыре, удвоив находящиеся в них гексаграммы и рассматривая новообразованные пары строящимися по принципу “переворачивания” (фань). Если тоже самое проделать с другими инвертными парами, то в целом порядок Вэнь-вана будет состоять из 36-ти пар, построенных по принципу “переворачивания” (табл. 2.11.7).

Таблица 2.11.7
1 часть (верхняя)	2 часть (нижняя)
111111-01 111111-01	000111-11 111000-12	100000-23 000001-24	011100-31 001110-32	011111-43 111110-44	001101-55 101100-56
000000-02 000000-02	111101-13 101111-14	111001-25 100111-26	111100-33 001111-34	011000-45 000110-46	110110-57 011011-58
010001-03 100010-04	000100-15 001000-16	100001-27 100001-27	101000-35 000101-36	011010-47 010110-48	110010-59 010011-60
010111-05 111010-06	011001-17 100110-18	011110-28 011110-28	110101-37 101011-38	011101-49 101110-50	110011-61 110011-61
000010-07 010000-08	000011-19 110000-20	010010-29 010010-29	010100-39 001010-40	001001-51 100100-52	001100-62 001100-62
110111-09 111011-10	101001-21 100101-22	101101-30 101101-30	100011-41 110001-42	110100-53 001011-54	010101-63 101010-64

Традиционно основной текст “Книги перемен” подразделяется на две неравномерные части: первая часть состоит из 30-ти гексаграмм, а вторая — из 34-х гексаграмм. При введении дополнительных гексаграмм (в первую часть — 6, во вторую — 2) весь их комплекс разделится на две равные части, состоящие каждая из 18-ти пар или 36-ти гексаграмм. В целом получится 72 гексаграммы. Все эти числа с нумерологической точки зрения достаточно интересные, а главное, они кратны числу шесть, соответствующему количеству черт в гексаграмме. 36 пар гексаграмм вписываются в матрицу 6 ´ 6. Кроме того, их можно связать с 36-ю десятидневками года. Каждой десятидневке будет соответствовать 12 черт, получаемых при сложении соответствующих пар гексаграмм. То, что при этом день не совпадает с чертой, можно компенсировать за счет проведения преобразований, подобных тем, при которых шесть стихий или “младших” триграмм сводятся к пяти стихиям.

При дальнейшем анализе преобразованного порядка Вэнь-вана следует исходить из того, что “малое является ценным в многочисленном; единое является главным во многом”. Данная формулировка известного ицзинистского правила была высказана ученым Ван Би (226—249) в его трактате “Чжоу и люэ ли” (“Основные принципы “Чжоу и””), где он указывает и на возможность его применения в отношении к структуре гексаграмм:

Если в данной гексаграмме пять [линий] Света и одна линия Тьмы, то одна [линия] Тьмы является в ней главным; если же пять [линий] Тьмы и одна — Света, то [линия] света является в ней главным (Ван Би 1936: 100).

Для триграмм одна черта (линия), противопоставленная двум другим, должна считаться главной. В гексаграммах не только одна противопоставленная черта, но и две будут главенствовать и определять полярность всего символа. Так, символ 001 будет янским, поскольку в нем имеется одна янская черта, а символы 101111 или 001111 будут иньскими, поскольку в них присутствуют соответственно одна и две иньских черт. Символы с одинаковым количеством янских и иньских черт будут равновесными. Символы, состоящие только из одного типа черт, триграммы и гексаграммы Цянь и Кунь, имеют соответственно полярности ян и инь.

Всего в набор 64-х гексаграмм входят:

1. 2 гексаграммы, составленные из 6-и знаков одного типа (прерывистые или сплошные черты);

2. 12 гексаграмм — 5-и одного типа и 1-го — другого;

3. 30 гексаграмм — 4-х одного типа и 2-х — другого;

4. 20 гексаграмм — 3-х одного типа и 3-х — другого.

Произведенное выше удвоение симметричных гексаграмм приводит к тому, что увеличивается до 4-х количество гексаграмм, состоящих из 6-ти черт одного типа, и до 36-ти — из 4-х черт одного типа и 2-х — другого типа.

При трансформации порядка Вэнь-вана в комплекс из 36-ти пар обратных гексаграмм в нем образуется некоторая избыточность. Действительно, зная первую гексаграмму в паре, ее можно автоматически, методом перевертывания, преобразовать во вторую гексаграмму. Само собой, вторая гексаграмма будет в той же степени янской или иньской, что и первая.

Введем “цену” каждой пары гексаграмм, выразив любую входящую в нее гексаграмму положительным или отрицательным числом, составляющим число янских или иньских главных линий (табл. 2.11.8). Так, например, гексаграмма 111111-01 будет иметь число “+6”, 010000-08 — число “+1”, 110011-61 — число “-2”, и т.д. Равновесные гексаграммы определяются числом [3], которое можно рассматривать и как положительное, и как отрицательное в зависимости от конкретного местоположения этих гексаграмм в порядке Вэнь-вана.

Таблица 2.11.8
1 часть (верхняя)	2 часть (нижняя)
	111111-01 +6		000111-11 +3		100000-23 +1		011100-31 +3		011111-43 [-1]		001101-55 +3
	000000-02 -6		111101-13 -1		111001-25 -2		111100-33 -2		011000-45 [+2]		110110-57 -2
	010001-03 +2		000100-15 +1		100001-27 +2		101000-35 +2		011010-47 +3		110010-59 +3
	010111-05 -2		011001-17 -3		011110-28 -2		110101-37 -2		011101-49 -2		110011-61 -2
	000010-07 +1		000011-19 +2		010010-29 +2		010100-39 +2		001001-51 +2		001100-62 +2
	110111-09 -1		101001-21 -3		101101-30 -2		100011-41 -3		110100-53 -3		010101-63 -3

Последнее требует разъяснения. Дело в том, что другие пары гексаграмм располагаются так, что их цены чередуются по своей полярности. Например, гексаграммы № 3—4 имеют цену “+2”, № 5—6 — цену “-2”, № 7—8 — цену “+1” и т.д. Исключение составляют пары № 43—44 и 45—46, которые имеют противоположные знаки, по сравнению с тем, что требовалось бы на их месте. Чтобы не нарушить ритм чередования янских и иньских пар, равновесным парам гексаграмм как раз и приписывается подходящая для их места полярность (рис. 2.11.19).

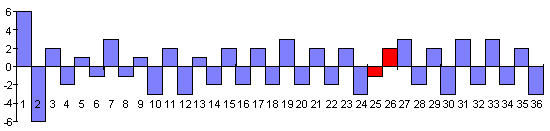
Рис. 2.11.19

Разумеется, подобная “ценовая” перекодировка пар гексаграмм выхолащивает их значения, поскольку при ней не учитываются различия в структуре тех или иных гексаграмм (например, гексаграммы 110110-57 и 011110-28 имеют одинаковую цену “-2”). Однако она позволяет выявить в порядке Вэнь-вана некоторые интересные закономерности (табл. 2.11.9).

Таблица 2.11.9
1 часть (верхняя)	2 часть (нижняя)	S 1	S 2
+6 (01/01)	+3 (11/12)	+1 (23/24)	+3 (31/32)	-1(43/44)	+3 (55/56)	+15
-6 (02/02)	-1 (13/14)	-2 (25/26)	-2 (33/34)	+2(45/46)	-2 (57/58)	-11	+17
+2 (03/04)	+1 (15/16)	+2 (27/27)	+2 (35/36)	+3 (47/48)	+3 (59/60)	+13
-2 (05/06)	-3 (17/18)	-2 (28/28)	-2 (37/38)	-2 (49/50)	-2 (61/61)	-13
+1 (07/08)	+2 (19/20)	+2 (29/29)	+2 (39/40)	+2 (51/52)	+2 (62/62)	+11	-17
-1 (09/10)	-3 (21/22)	-2 (30/30)	-3 (41/42)	-3 (53/54)	-3 (63/64)	-15
	-1	-1		+1	+1
	-2			+2

Оказывается, что первая и вторая части таблицы симметричны по суммам цен как в целом, так и по отдельным столбцам. При этом первая ее часть является иньской, а вторая — янской по знаку. Также своеобразная симметрия по суммам цен наблюдается и в строках таблицы. На этот раз верхняя часть из трех строк является янской, а нижняя — иньской. Общие суммы цен как по столбцам, так и по строкам равны нулю. Подобного рода симметрии наблюдаются еще при размещении 36-ти пар гексаграмм в таблицах 18 ´ 2, 9 ´ 4 и 3 ´ 12. Таким образом, порядок Вэнь-вана предстает как сложносбалансированная система.

Дата добавления: 2015-07-12