Алгоритмы, структуры данных и методология видеоигр

Пришло время поговорить о том, как же собрать воедино все, о чем рассказывалось в предыдущих главах этой книги, чтобы получить в результате настоящую компьютерную игру- Компьютерная игра —программа синергистическая, она не является просто совокупностью своих частей. Игра должна на время поместить игрока в другую реальность. Причем этот другой мир будет существовать только в компьютере и сознании игрока. Чтобы достигнуть этого мы должны понять, как зрительно и эмоционально воспринимает игру сам игрок, и на основании этого выработать подходящую концепцию архитектуры компьютерной игры. В этой главе мы затронем множеством, не всегда связанных между собой, но несомненно важных, если, конечно, вы все еще хотите превратить те смутные очертания, которые возникают в вашем воображении, в захватывающую компьютерную игру.

В этой главе много неочевидных выводов и намеков, поэтому читайте внимательно! Основные темы этой главы:

§ Структуры данных для представления игрового пространства;

§ Столкновения объектов;

§ Представление игровых объектов;

§ Структуры данных в компьютерных играх;

§ Клонирование игровых объектов;

§ Состояния объектов;

§ Пользовательский интерфейс;

§ Демонстрационные режимы;

§ Сохранение состояния игры;

§ Моделирование настоящего мира.

Структуры данных, используемые для представления игрового пространства

Если бы мы решили воссоздать некий мир во всех его подробностях, то эта глава заняла бы, наверное, миллион страниц. Поэтому в играх мы имеем дело с приближенной к действительности реальностью. Зачем нам создавать весь мир в нашей игре? Нам достаточно смоделировать только то, что имеет непосредственное отношение к сюжету.

Поскольку в качестве прообраза нашей игры мы выбрали Wolfenstein и DOOM, давайте поговорим о том, как создавался мир этих игр. А затем используем эту концепцию как фундамент для нашей собственной компьютерной игры. Но прежде чем сделать это, вкратце обсудим «стандартные» способы представления трехмерного мира на основе многоугольников.

В качестве примера возьмем гипотетические трехмерные скачки. В такой игре нам понадобятся деревья, дома, беговая дорожка, трибуны и пункт контроля. При стандартном способе представления пространства, состоящего из многоугольников, эта информация должна быть представлена на уровне объектов, то есть для каждого трехмерного объекта нам потребуется его модель. Эти модели будут представлены в виде списка многоугольников, заданных их вершинами. Затем каждому объекту надо будет сопоставить координаты, ориентацию и масштаб. Следовательно, если мы хотим, чтобы у нас было десять разных зданий, мы должны определить десять разных объектов: по одному на каждый тип зданий. Затем мы можем взять каждый объект и создать связанный список.

Завершив список, мы получим возможность строить (или визуализировать) каждый объект. Подобные же списки следует создать для структур данных деревьев, трибун и т. д.

Наконец, непрерывная беговая дорожка будет представлена списком прилегающих многоугольников. Таким образом, весь мир игры будет представлен в виде списков объектов. На рисунке 11.1 показана схема такого обьектно-прогтуанственного представления игрового пространства.

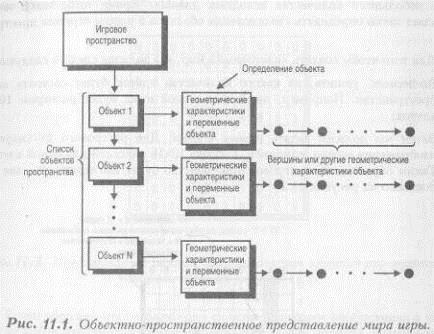
Это неплохой и вполне рабочий способ представления мира. Однако, представляя игровое пространство подобным образом, достаточно сложно определять столкновения объектов, создавать новые уровни и хранить данные. В компьютерных играх желательно иметь возможность быстро создавать новые Уровни на основе простых элементов. Поэтому стоит взглянуть на структуры Данных и методы их представления с точки зрения простоты создания нового варианта игрового пространства. Используя такой подход, мы можем проиграть в гибкости, но это окупится долгой жизнью игры.

Возьмем тот же пример скачек, реализуем его в виде двухмерного пространства, а затем придадим ему видимость трехмерности. В четырнадцатой главе, «Связь», мы подробно рассмотрим создание законченной компьютерной игры с «клеточным» пространством. Сейчас же просто попробуем разобраться в том, что собой представляет этот метод.

В большинстве компьютерных игр различные объекты и изображения многократно повторяются в разных комбинациях. Если вы внимательно посмотрите на игру РасМап, то заметите, что, несмотря на обилие лабиринтов, каждый из них состоит из одних и тех же объектов. Это таблетки, которые возвращают игроку силу, точки, повороты налево и направо, прямые стены и так далее, Пристальный анализ каждого экрана игры РасМап, покажет вам, что вся графика составлена из ряда «клеточек». Эти «клетки» в совокупности образуют повороты, прямые ходы и все остальное. Преимущество такого метода заключается в том, что он позволяет создать большой и разнообразный мир на основании очень небольшого количества исходных данных- Кроме того, такой метод позволяет легко определять столкновения объектов в нашем игровом пространстве.

Для того чтобы создать «клеточный» мир, мы должны сделать следующее:

§ Во-первых, решить, из какого количества клеток будет состоять наше пространство. Например, пусть мир нашей игры будет размером 10х10 клеток;

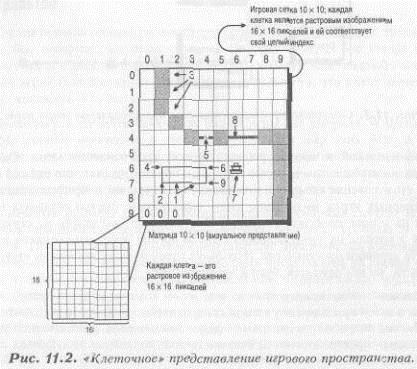
§ Затем мы должны задать размер клетки. Для растрового двухмерного изображения можно, например, выбрать 16х16 пикселей для одной клетки. Таким образом, наше игровое пространство будет выглядеть так, как это показано на рисунке 11.2.

§ Затем мы должны нарисовать варианты клеток для нашей игры. Мы можем нарисовать клетки, содержащие изображения маленького дерева, стены, еды и так далее;

§ После этого мы должны пронумеровать фрагменты. Таким образом, у каждого из них будет свой целочисленный идентификатор;

§ Затем мы должны задать структуру данных (обычно в виде двухмерной матрицы) и заполнить ее соответствующими идентификаторами.

Преставление данных для нашего примера «клеточного» игрового пространства показано на рисунке 11.3.

Таким образом, мы разбили одно сложное растровое изображение в нашей игре на набор фрагментов. Затем мы'создали игровую матрицу, которая задает растровое изображение как совокупность определенных фрагментов, используя Для их идентификации целые числа (идентификаторы фрагментов),

Теперь мы можем легко визуализировать игровое пространство: у нас есть его матрица, по которой несложно выбрать необходимые фрагменты изображения. Мы также имеем сами эти фрагменты (клетки). Фактически, мы просматриваем матрицу, клетка за клеткой, и в соответствии с идентификаторами воссоздаем необходимое растровое изображение.

На рисунке 11.4 показано построение растрового изображения «клеточного» игрового пространства.

Как вы можете видеть из рисунка 11.4:

§ Мы заполнили структуру данных игры (обычно это двухмерная матрица) Целыми числами, причем каждое число - это идентификатор того фрагмента, изображение которого мы хотим поместить в соответствующей клетке;

§ Затем во вложенном цикле определяем идентификаторы клеток пространства;

§ В соответствии с каждым идентификатором визуализируем необходимый фрагмент растрового изображения. Несколько таких фрагментов будут составлять изображение здания, дороги, объекта игры и т. д.

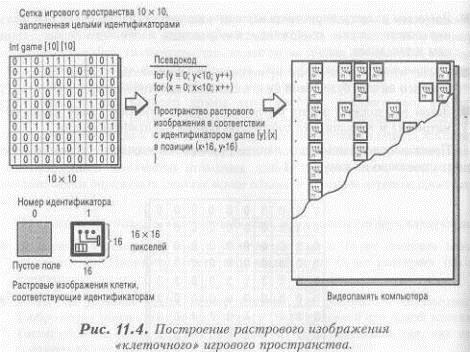
Мы должны только побеспокоиться о правильном позиционировании каждого фрагмента. В нашем примере при переходе к следующей клетке мы должныпередвигаться сразу на величину размера клетки, то есть на 16 пикселей.Нарисовав весь экран (10х10 клеток), мы получим растровое изображение160х160 пикселей.

Используя клеточное построение игрового пространства, легко создавать новые уровни в игре. Более того, такой метод упрощает создание инструментов для изготовления новых игровых пространств. Несложно написать программу, которая будет рисовать на экране сетку, а затем с помощью пиктограмм или цветов представлять то растровое изображение игрового пространства, которое вам нужно. То есть вы размещаете пиктограммы или помечаете цветом нужные клетки, а программа транслирует их в соответствующие идентификаторы фрагментов и записывает результирующую матрицу. Таким образом, в рекордно короткие сроки можно создать десятки различных уровней для своей игры, причем каждый из них займет минимум оперативной памяти.

Единственный недостаток данного метода заключается в том, что мы не можем поместить объект в произвольное место. Он обязательно должен вписываться в границы клетки. Однако обычно это не является проблемой.

Подобная техника была использована в DOOM и Wolfenstem. Только вместо фрагментов, представляющих плоское растровое изображение, там используются трехмерные кубы, составленные из одной или нескольких текстур. Создавая нашу игру, мы можем поступить так же.

Если вы играли в Wolfenstein, то наверняка заметили, что мир этой игры создан с - помощью набора кубов, которые покрыты текстурой с четырех вертикальных сторон. Каждый из этих кубов в действительности является клеткой в двухмерной решетке. Идентификаторы каждого модуля задают текстуры, которые будут расположены соответственно по четырем сторонам. Программа считывает эти значения и на их основании создает трехмерный мир.

Создать трехмерный мир с помощью двухмерной решетки помогает её регулярная структура и одинаковая высота всех кубов. Таким образом, подобное игровое пространство получается как бы в результате экструзии плоского клеточного мира.

Клеточное пространство удовлетворяет практически всем требованиям реальной игры. Однако иногда вам могут потребоваться некоторые дополнительные возможности, которые мы уже разбирали при обсуждении объектно-пространственного метода (метода многоугольников). С помощью клеточного подхода удобно создавать окружающую среду игры. Однако иногда ограничения этого метода делают невозможным создание определенных типов объектов, и тогда целесообразно использовать другую структуру данных. Например, иная структура просто необходима, если по ходу игры требуется размещать мелкие объекты в произвольных местах.

В трехмерном мире DOOM также имеются двухмерные стационарные объекты, такие как еда, оружие и т. д. Я подозреваю, что эти объекты имеют другую структуру данных, возможно связанную с конкретным помещением. Эта дополнительная структура данных задает определенное положение и тип объекта, который может быть расположен в данной комнате.

В любом случае, используйте те методы, которые позволяют реализовать ваши замыслы. Однако не забывайте о том, что новые уровни и новые объекты Должны создаваться как можно более простым путем. Вы не должны каждый Уровень строить с нуля. Вы должны иметь для этого инструменты и максимально использовать уже готовые элементы.

Теперь, создав игровое пространство, посмотрим как его объекты взаимодействуют между собой.

Когда объекты сталкиваются

В общем случае столкновение объектов происходит тогда, когда занимаемые ими пространства пересекаются (см. рис. 11.5).

Однако для игр на персональных компьютерах вычисление области пересечения произвольных изображений потребует слишком много времени. Поэтому большинство программистов используют в подобных расчетах описывающие прямоугольники, то есть минимальные прямоугольники, в которые помещается весь объект.

Контролировать столкновения между прямоугольниками намного проще. Например, пусть даны прямоугольники R1 и R2. Алгоритм 11.1 контролирует их столкновение.

Дата добавления: 2015-07-12