Читайте также:
|
Издержки производства и себестоимость единицы продукции А по трем заводам характеризуются следующими данными:
Таблица 5.5.
| Номер завода | Издержки производства, тыс.руб. | Себестоимость единицы продукции, руб. |
Исчислим среднюю себестоимость изделия по трем заводам. Как и прежде, главным условием выбора формы средней является экономическое содержание показателя и исходные данные.
Издержки производства
Средняя себестоимость = ----------------------------------------
единицы продукции (
) Количество продукции
руб.
Таким образом, формулу для расчета средней гармонической взвешенной можно представить в общем виде:
Мода.
Характеристиками вариационных рядов, наряду со средними, являются мода и медиана.
Мода - это величина признака (варианта), наиболее часто повторяющаяся в изучаемой совокупности. Для дискретных рядов распределения модой будет значение варианта с наибольшей частотой.
Пример 8.
Распределение проданной обуви по размерам характеризуется следующими показателями:
| размер обуви | и выше | ||||||||||
| число пар, в % к итогу | — | — |
В этом ряду распределения мода равна 41. Именно этот размер обуви пользовался наибольшим спросом покупателей.
Для интервальных рядов распределения с равными интервалами мода определяется по формуле:
где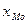 
- начальное значение интервала, содержащего моду;
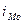- величина модального интервала;
- частота модального интервала;
- частота интервала, предшествующего модальному;
- частота интервала, следующего за модальным.
Дата добавления: 2015-07-12; просмотров: 55 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Пример 6. | | | Пример 9. |