Законы распределения, используемые в теории надежности. Оценка основных показателей надежности в период нормальной эксплуатации.

Биноминальный закон распределения числа n – появления события А в m – независимых опытах (испытаниях). Если вероятность появления события А в одном испытании есть р, тогда вероятность не появления события q = 1 – p.

Если независимое число испытаний = m, тогда вероятность появления n событий будет равна: - уравнение Бернулли.

Закон Пуассона.

вероятность возникновения случайного события n раз за время t.

Экспоненциальный закон.

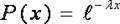
где P(x) это вероятность того что случайная величина X имеет значение большее x.

g распределение.

Если отказ устройства возникает тогда когда произойдет не менее k отказов его элементов, а отказы элементов подчинены экспоненциальному закону с параметром l0. Плотность вероятности отказа устройства:

Распределение Вейбула.

Плотность вероятности:

Нормальное распределение (НР).

Случайная величина X возникает тогда когда x зависит от большого числа однородных по своему влиянию случайных факторов, причем влияние каждого из факторов по сравнению с влиянием совокупности остальных незначительно.

Плотность вероятности отказа НР: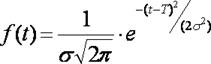

c² – распределение.

Если случайная величина t распределена по НЗ с Т = 0 и = 1, то параметр X = будет являться случайной величиной с плотностью распределения:

После периода приработки начинается период нормальной эксплуатации, когда интенсивность отказов падает λ(t) и в течение длительного времени остается примерно постоянной. В этот период происходят внезапные отказы, которые носят случайный характер, например из-за случайного повышения нагрузок. Распределение наработки до отказа описывается показательным законом. При этом функция плотности распределения

f(t) = Xexp(-Xt). Вероятность безотказной работы P(t) = exp{-Xt).

При постоянной интенсивности отказов средняя наработка на отказ равна Т = 1/Х.

Дата добавления: 2015-07-12