While (i>1) And (A[i Div 2]<x) Do Begin

A[i]:=A[i Div 2];

i:=i Div 2;

End;

A[i]:=x;

End;

Биномиальная куча

Биномиальная куча (H) – это очередь с приоритетом, в которой, помимо эффективного выполнения операций: Insert (H, x) – вставка элемента в очередь; Extract _ Min (H) – извлечение минимального элемента из очереди, эффективно выполняется и операция Merge (H ₁, H ₂, H ₃) – слияния двух куч в одну.

Биномиальная куча строится из биномиальных деревьев (B). На рис. 7.8 показаны биномиальные деревья B ₀, B ₁, B ₂, B ₃, B ₄ и B ₅.

Рис. 7.8. Биномиальные деревья B ₀, B ₁, B ₂, B ₃, B ₄ и B ₅

Биномиальная куча (H) – это некая совокупность биномиальных деревьев. В вершинах деревьев записаны ключи, причем в корне каждого дерева записан наименьший ключ, и ключ вершины-родителя всегда меньше ключей сыновей. Основополагающим для биномиальной кучи является условие о том, что в ней нет двух одинаковых биномиальных деревьев (с одной степенью корня).

Пусть в куче n элементов. Представим n в двоичной системе (представление однозначное) – , где все i ₁, i ₂, …, i_k различны. Тогда в куче будут деревья , каждое из которых содержит соответствующее количество элементов, составляющих кучу.

Пример (рис. 7.9). Пусть n =11 – куча с 11 вершинами. В двоичной системе счисления 11₁₀=1011₂, и H состоит из B ₀, B ₁ и B ₃.

Рис. 7.9. Пример биномиальной кучи

В п. 5.3 для представления деревьев использовался принцип «левый сын и правый брат», и его разумно использовать (ввиду необходимости выполнения операции Merge) при работе с биномиальными деревьями. Кроме того, корни биномиальных деревьев связаны в корневой список в порядке возрастания степеней. Структура элемента кучи показана на рис. 7.10.

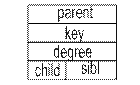
Рис. 7.10. Структура элемента кучи

Её формализованная запись имеет вид:

Type pt=^el;

el= Record

parent:pt;

key: Integer;

degree: Integer;

child,sibl:pt;

End;

Var head:pt;{Указатель на первый корень кучи.}

В ней parent – указатель на вершину родителя; key – значение ключа; degree – степень вершины; child – указатель на самого левого сына вершины; sibl – указатель на правого брата вершины или, в случае корневого списка, указатель на следующий элемент списка. Для примера на рис. 7.9 его описание в памяти представлено на рис. 7.11.

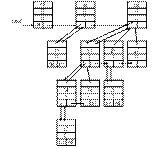
Рис. 7.11. Представление кучи в памяти компьютера

Рассмотрим операции с биномиальной кучей и начнем с Merge (head 1, head 2, head). Для ее реализации потребуются две вспомогательные процедуры. Первая – слияние двух биномиальных деревьев одного размера B_{k -1} в дерево B_k. Ситуация на уровне примера для деревьев второго порядка проиллюстирована на рис. 7.12, а её формализованная запись имеет вид:

Procedure Link(x,y:pt); {x, y – указатели на корни деревьев.}

Begin

x^.parent:=y; {1}

x^.sibl:=y^.child; {2}

y^.child:=x; {3}

y^.degree:=y^.degree+1;

End;

Рис. 7.12. Слияние двух биномиальных деревьев

Вторая вспомогательная процедура, назовем её, например, Coufl, сливает два корневых списка куч H ₁ и H ₂, отсортированных по значению degree, в один список, отсортированный в порядке неубывания степеней вершин. Пример слияния двух списков приведен на рис. 7.13. В кружках указаны степени корневых вершин, а пунктирными линиями показаны связи в результирующем списке.

Procedure Coufl(x,y:pt; Var z:pt);

Begin

Дата добавления: 2015-07-11