Очереди с приоритетами

Двоичная куча и пирамидальная сортировка

Двоичную кучу, или пирамиду, можно определить как двоичное дерево, в котором значение ключей у потомков (непосредственных, то есть детей) не больше ключа вершины. Это свойство выполняется для всех вершин дерева, не являющихся листьями. В дереве, являющемся кучей, все уровни, кроме, может быть, последнего, заполнены полностью. При представлении двоичной кучи в виде массива (A) вершине с номером i соответствует элемент A [ i ] (значение ключа), а детям вершины – элементы A [2* i ] и A [2* i +1]. Отсюда следует, что должны выполняться неравенства A [ i ]≥ A [2* i ] и A [ i ]≥ A [2* i +1]. Таким образом, следует говорить так: элементы массива А образуют (являются) двоичную кучу, если удовлетворяют названным требованиям для всех значений i.

Пример. На рис. 7.1 приведено изображение двоичной кучи в виде дерева и массива.

Рис. 7.1. Двоичная куча: а) представление в виде дерева; б) представление в виде массива. В вершинах дерева указаны значения ключей, а рядом с ними – индексы элементов массива

Сформулированное свойство кучи задает некое отношение порядка на множестве элементов. Однако куча должна обладать еще одним свойством, назовем его «формой». Идея формы лучше всего разъясняется графически – рис. 7.2.

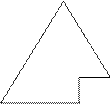
Рис. 7.2. Форма кучи

Таким образом, двоичное дерево, являющееся кучей, имеет свойство формы, если листья дерева находятся не более чем на двух уровнях, причем находящиеся на нижнем уровне вершины (листья) группируются слева. Так двоичное дерево, удовлетворяющее первому свойству – есть отношение порядка, но имеющее форму, графическое изображение которой приведено на рис. 7.3, не является кучей. В куче нет незанятых вершин, и если она содержит n вершин, то ни одна из них не может отстоять более чем на log ₂ n от корня.

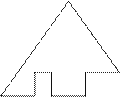
Рис. 7.3. Двоичное дерево, не являющееся кучей

Рассмотрим представление двоичной кучи в виде массива. Пусть дан произвольный массив и из него требуется сделать кучу. Элементы массива с индексами от n Div 2 + 1 по n образуют кучу по той простой причине, что удвоение индекса выводит нас за пределы массива. А затем, начиная с элемента A [ n Div 2] и заканчивая элементом A [1], последовательно находим в построенной части кучи место для очередного элемента так, чтобы выполнялось свойство кучи и он – элемент – был в составе кучи. Если мы скажем, что процедура Push (i,n) ответственна за нахождение места для элемента A [ i ] в куче, то формализованная запись логики выглядит так:

Procedure BuildHeap;

Var i: Integer;

Begin

For i:=n Div 2 DownTo 1 Do Push(i,n);

End;

Procedure Push(r,t: Integer);

Var i,j,v: Integer;

pp: Boolean;

Begin

v:=A[r]; {Запоминаем элемент.}

i:=r; {Индекс рассматриваемого элемента.}

j:=2*i;{Индекс элемента, с которым происходит сравнение.}

pp:= False;{Считаем, что для элемента не найдено место в куче.}

While (j<=t) And Not pp Do Begin

If (j<t) And (A[j]<A[j+1]) Then j:=j+1;{Сравниваем с большим элементом.}

If v>=A[j] Then pp:= True {Место для A[r] найдено.}

Else Begin {Переставляем элемент с номером j на место i и идем дальше по массиву.}

A[i]:=A[j];

i:=j;

j:=2*i;

End;

End;

A[i]:=v; {Записываем A[r] на найденное для него место в куче.}

End;

Формализованная запись метода пирамидальной сортировки следующая:

Procedure Sort;

Var t,w,i: Integer;

Begin

t:=n Div 2+1;{Эта часть массива является кучей.}

For i:=t-1 DownTo 1 Do Push(i,n);{Формирование кучи (только один раз).}

For i:=n DownTo 2 Do Begin

w:=A[1];

A[1]:=A[i];

A[i]:=w; {Меняем местами первый и i-й элементы.}

Push(1,i-1); {«Проталкиваем» первый элемент.}

End;

End;

Нашей следующей задачей является рассмотрение представления кучи в виде двоичного дерева (рис. 7.1а). Пусть есть двоичное дерево и его требуется преобразовать в двоичную кучу. Описание вершины дерева традиционно:

Type pt=^el;

el= Record

data: Integer;

left,right:pt;

End;

Var root:pt;{Указатель на корень дерева.}

Function Tree(t: Integer):pt;

Var x: Integer;

w:pt;

Begin

If t=0 Then Tree:= nil {Нулевое количество вершин определяет ссылку типа nil.}

Дата добавления: 2015-07-11