Постановка задачі

Домашнє завдання №2

по дисципліні “Організація ремонтного виробництва”

Постановка задачі

За даними одномірного інтервального часового ряду (ЧР), які наведені у відповідному варіанті, необхідно:

– провести згладжування ЧР за допомогою методу ковзної середньої (МКС) та методу експоненціального згладжування (МЕЗ);

– визначити аналітичні моделі тренду початкового та згладжених ЧР, отриманих за двома вказаними вище методами;

– надати порівняльну точнісну оцінку отриманим моделям і обрати серед них найбільш точну;

– визначити за отриманою прогнозною моделлю момент демонтажу з борту літака блоку, який знаходиться у передвідмовному стані.

Для виконання поставленого завдання використати матеріали лекційного заняття по темі 4.

Методичні вказівки до виконання домашнього завдання №2.

1. Для проведення згладжування початкового ЧР за МКС інтервал згладжування 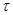заданий у варіанті завдання. Значення 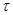задане як число і, яке характеризує множник у формулі 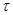= і × _, де - часовий такт ряду. За результатами обчислень згладжених значень рівнів нового ЧР побудувати його графік.

2. Для МЕЗ початкового ЧР використати формулу

,

де 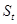- значення рівня ЧР, який підлягає експоненціальному згладжуванню в момент ; - значення рівня ЧР для моменту , який був попередньо згладжений експоненціально; - значення рівня початкового ЧР в момент ; - параметр згладжування. За базовий рівень прийняти перший член початкового ЧР, тобто . Значення параметра задано у варіанті завдання. За результатами обчислень значень рівнів згладженого ЧР побудувати його графік.

3. За допомогою програми STATISTICA визначити аналітичні моделі трендів для початкового та двох згладжених ЧР.

3.1. Ввести дані до файлу даних STATISTICA, для чого

а) організувати файл даних:

- увійти до програми, обрати на верхній панелі команду FILE (Файл), у ній - опцію NEW (Новий), занести необхідну кількість стовпців і рядків і натискаємо OК.

б) занести дані до створеного файлу

Для занесення даних рекомендується така структура їх організації:

Номер елементу ЧР (VAR1)	Рівні початкового ЧР (VAR2)	Рівні ЧР, згладженого за допомогою МКС (VAR3)	Рівні ЧР, отриманого за МЕЗ (VAR4)
…

в) записати файл даних на диск

Щоб зберегти дані у файлі під оригінальним ім’ям обираємо FILE, потім натискаємо SAVE AS (зберегти як), вносимо його ім'я і вказуємо місце, де він буде зберігатись.

3.2. Визначити моделі трендів по кожному ЧР, для чого використати на верхній панелі програмного меню команду «Графики»

Вхід до необхідної функції програми показано на рисунку нижче.

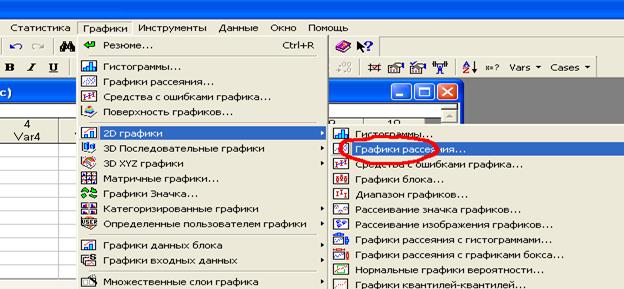
У опції “Quick” за допомогою кнопки “Variables” ввести масиви даних, для яких буде здійснюватися побудова моделі тренду, При цьому для змінної “X” постійно буде використовуватися дані колонки 1 (VAR1), а для змінної “Y” - почергово VAR2, VAR3 та VAR4. У вікні “Graph type” необхідно встановити режим “Regular”, після чого натиснути ОК. Для дослідження даних кожного ЧР обрати опцію “Advanced” у верхньому меню функції. Після входу цю опцію для обраного за координатою “Y” ЧР виконати підбір моделі тренду, задаючи послідовно у вікні “Fit” типи моделей “Linear”, “Logarithmic” та “Exponential”. Після кожного введення – натискати кнопку ОК та отримувати графік тренду ЧР. У верхній частині малюнку надається аналітичний вираз, який і є моделлю тренду. Серед трьох випробуваних варіантів моделей обрати найточнішу апроксимацію, зафіксувати її у графічному файлі та роздрукувати. Ті ж самі дії виконати для інших ЧР.

4. Для проведення порівняльної оцінки точності отриманих моделей трендів необхідно:

4.1. Заповнити даними таблицю, форма якої наведена нижче

№

Види ЧР та трендів та їх точнісні характеристики

Дані ЧР та трендів

Початковий ЧР

Тренд початкового ЧР

Відносне відхилення точок ЧР та його тренду

Квадрат відхилення

Сума квадратів відхилень

ЧР за МКС

Тренд ЧР за МКС

Відносне відхилення точок ЧР та його тренду

Квадрат відхилення

Сума квадратів відхилень

ЧР за МЕЗ

Тренд ЧР за МЕЗ

Відносне відхилення точок ЧР та його тренду

Квадрат відхилення

Сума квадратів відхилень

і по сумі квадратів відхилень вказати на найбільш точний варіант апроксимації тренду ЧР.

4. Визначення моменту виведення з експлуатації технічного пристрою.

За наданим у варіанті завдання гранично допустимим значенням 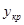параметру прогнозу визначити момент часу експлуатації, у який даний буде потребувати проведення відновлення. Цей момент визначається шляхом підстановки у отримане рівняння тренду заданого значення 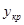та розв’язку отриманого рівняння відносно змінної t.

Дата добавления: 2015-07-11