ИССЛЕДОВАНИЕ шероховатости поверхности дорожек качения приборных подшипников оптико-электронным методом

В статье предложен оптико-электронный метод исследования шероховатости поверхностей дорожек качения приборных подшипников после финишной обработки.. Метод основан на определении автокорреляционных функций с использованием квазиоптимального корреляционного алгоритма. Приведены результаты исследования шероховатости поверхности после шлифования абразивными кругами.

Качество поверхности дорожек качения приборных подшипников, с точки зрения шероховатости поверхности, во многих случаях является определяющим фактором, влияющим на долговечность и надежность подшипников при их эксплуатации, а также на точность показаний приборов, имеющих в своём составе эти подшипники.

В настоящее время оценку параметров микрорельефа различных поверхностей деталей машин и механизмов во многих случаях выполняют с помощью измерительных оптико-электронных преобразователей, используемых совместно со средствами компьютерной обработки сигналов [1-4]. Отмечая несомненные достоинства данных методов оценки параметров микрорельефа, следует отметить и их недостатки. Так, например, в [1,2] требуется использовать источники освещения исследуемой поверхности когерентные как во времени, так и в пространстве. В других же работах [3,4] требуется применение двух световых потоков, из которых первый (опорный) служит для освещения исследуемой поверхности, а второй используется для компенсации флуктуаций мощности опорного потока. Отмеченные недостатки существенно усложняют контрольно-измерительную аппаратуру данного назначения, а также её использование непосредственно на рабочем месте при изготовлении различных изделий. В большинстве случаев все эти усложнения, вносимые в аппаратуру, предназначены для компенсации дополнительной погрешности измерения параметров микрорельефа, возникающей вследствие отклонения опорного светового потока от его номинального значения.

Устранения отмеченных недостатков было выполнено с использованием оптико-электронного комплекса [5,6], который включал в себя оптическую систему, видеокамеру, компьютер и специально разработанный алгоритм обработки изображения исследуемой поверхности. Для теоретического и практического обоснования предлагаемой методики устранения дополнительной погрешности оптико-электронный комплекс авторами работы [7] был представлен в виде структуры информационно-измерительной системы (ИИС), которая показана на рис.1.

Рис.1. Структура ИИС оценки параметров микрорельефа

Она состоит из выделенной площади ВП исследуемой части поверхности, источника опорного светового потока ИСП, видеокамеры ВК и блока цифровой обработки сигналов БЦОС. Система состоящая из ИСП и ВК может рассматриваться как оптико-электронный измерительный преобразователь (ИП). Совокупность ИСП и ВП образует канал первичного рельефно-оптического преобразования. Входная величина, воздействующая на вход оптико-электронного ИП, формируется на исследуемой ВП, в которую входят – типов элементарных площадок с различным микрорельефом. Её можно представить как среднее арифметическое

= ,

где – -тый компонент входной величины преобразуемого параметра микрорельефа, например, ; – весовой коэффициент, соответствующий доле элементарных площадок ВП с микрорельефом – того типового уровня (при общем числе типовых уровней ). Набор значений { } определяется конкретным характером механической обработки ВП.

Выходом ИСП является величина опорного светового потока . Её действие на -тую элементарную площадку ВП вызывает появление соответствующего отражённого светового потока величины 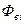. Таким образом, каждой -той элементарной площадке ВП соответствует, во-первых, один из выходов канала первичного рельефно-оптического преобразования – величина 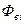, воздействующая, в свою очередь на входы ПЗС-матрицы, и, во-вторых, определённый электрический сигнал ПЗС-матрицы.

Номинальная функция преобразования -того компонента входной величины для ИП указанного типа, соответствующего -тому подмножеству одинаково обработанных элементов ВП может быть представлена как

= =( ) ( / )=( ) =

= ( ) ()

≤ ≤ ,

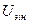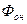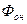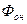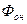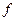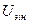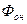где – коэффициент физического преобразования светового потока в электрический сигнал ПЗС-матрицы, который в используемых диапазонах изменений измеряемой величины и опорного светового потока от них не зависит; – номинальное значение величины ; – номинальное значение отражённого светового потока 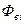, поступающего от любого элемента из -того подмножества площадок ВП; , – границы используемого диапазона изменений ; 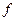() – функциональная зависимость номинальных значений нормированного выхода канала первичного рельефно-оптического преобразования от -того компонента измеряемой величины . Другими словами, – характеризует отражательную способность -того компонента ВП при воздействии на ВП номинального опорного светового потока 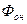. Для конкретных образцов, приведенных на рис.4, , 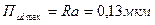. Саму же функцию 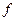() можно аппроксимировать полиномом степени :

()= ,

где 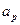– степенной коэффициент аппроксимации.

При исследовании влияния мощности опорного светового потока на характеристики видеосигнала в работе [7] участок анализируемой поверхности размером считывался по строкам и столбцам строчно-кадровым растром черно-белой телевизионной передающей камерой с ПЗС–матрицей и аналогово-цифровым преобразователем. Таким образом, в запоминающем устройстве БЦОС формировался кадр исходного полутонового изображения поверхности формата точек дискретизации – пикселей. Сигнал яркости каждого пикселя принимал значения, лежащие в диапазоне 0 – 255 от. ед.

За номинальное значение опорного светового потока была принята величина 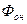=600 лм, а для величин , – значения 200 лм и 1000 лм соответственно. Выбранный диапазон значений вполне соответствует рабочим значениям светового потока, которые могут встретиться в практике применения рассматриваемых ИИС в заводских условиях. Изменения светового потока в этом случае могут происходить по разным причинам, например, вследствие колебаний напряжения питания источников света, изменения прозрачности атмосферы на рабочем месте при выполнении технологического процесса изготовления изделия, неконтролируемых бликов на исследуемой поверхности от посторонних источников света и т.п. Все эти непредусмотренные воздействия на освещённость исследуемой поверхности можно охарактеризовать с помощью функции влияния согласно ГОСТ 8.009 − 72 “Нормируемые метрологические характеристики. Средства измерения”. Проведёнными исследованиями, выполненными в работе [7], было установлено, что функция влияния носит мультипликативный характер. Обозначив через отклонение опорного светового потока от своих номинальных значений как = – 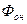, а через () – мультипликативную функцию влияния отклонений типа на результаты измерительных преобразований , ( =1,…, ), реальную функцию оптико-электронного преобразования -того компонента измеряемой величины, в отличие от номинальной, можно выразить следующим образом:

=( ) ( / )=( ) =

=( ) () ()

≤ ≤ , ≤ ≤ ,

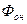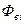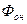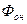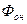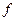С любой практически требуемой точностью введённая выше функция влияния может быть аппроксимирована полиномом некоторой степени :

()=1+ ,

где 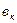– коэффициент при степени , определяемый согласно экспериментальным данным. Отметим, что данная функция принимает единичное значение при номинальном значении опорного светового потока .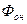

Наличие мультипликативного характера функции (), содержащейся в выражении выходной электрической величины оптико-электронного ИП, диктует выбор логометрического способа устранения рассматриваемой дополнительной погрешности [8]. Однако традиционное применение логометрирования предусматривает введение в состав ИИС дополнительного осветительного канала и второй ПЗС-матрицы, содержащих компенсационные величины, что существенно усложняет и увеличивает габариты ИИС.

Поэтому применительно к используемой разновидности измерительного преобразования в [7] был выдвинут новый принцип коррекции дополнительной погрешности, вызываемый нестабильностью опорного светового потока.

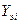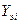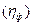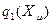
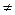
Такой принцип был сформулирован в форме требования соблюдения однозначных соответствий между набором величин ( (), =1,…, ), и двумя функционалами ( (), =1,…, ), =1,2, множества значений которых связываются с измеряемыми и влияющими величинами произведениями вида , где – функциональная зависимость, отвечающая неравенству 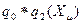; 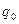=const

При реализации частного

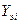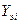( (), =1,…, )/ ( (), =1,…, ) (1)

одинаковые мультипликативные компоненты числителя и знаменателя 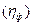сокращаются. Следовательно, реализация отношения (1) не ведёт к увеличению габаритов создаваемой ИИС, так как в формировании каждого функционала ( =1,2) будет использован один и тот же набор величин .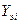

Реализация предлагаемого способа коррекции дополнительной погрешности в предлагаемой работе была осуществлена с привлечением теории оптимальной линейной фильтрация сигналов известной формы [9]. Как было уже отмечено выше, использование данного оптико-электронного комплекса обеспечивает формирование в памяти БЦОС полутонового изображения исследуемой поверхности формата точек дискретизации. Следовательно, к этому двумерному массиву можно применить известные методы цифровой обработки сигналов [10,11]. Сам принцип базируется на разработке метода определения неизвестной шероховатости исследуемой поверхности на основе сравнении изображения этой поверхности с изображениями образцовых поверхностей, для которых определены параметры шероховатости по известным гостовским методикам [12]. В результате сравнения определяется, какой образцовой поверхностью с заданной вероятностью распознавания соответствует исследуемая поверхность, что можно рассматривать как процесс отождествления анализируемого изображения поверхности с одним из элементов множества эталонных изображений с различным микрорельефом. Таким образом, в предлагаемом методе определяется совпадение этой поверхности с одной из образцовых поверхностей и делается вывод, что она имеет такие же параметры шероховатости, как и образцовая поверхность. В качестве критерия сравнения неизвестной шероховатости исследуемой поверхности с шероховатостями эталонных поверхностей в работе [7] был предложен коэффициент корреляции, вычисляемый по классической формуле [10]

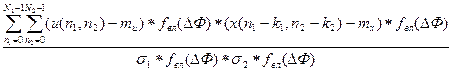= (2)

по полутоновому изображению исследуемой поверхности, предварительно записанного в память БЦОС. Здесь через обозначен фрагмент изображения (эталон), который расположен внутри зоны поиска 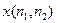, а и 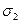− средние квадратические отклонения величин и 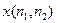от их математических ожидани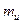й и соответственно, определяемые по формулам

= и = .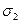

В этих формулах − количество точек дискретизации в сравниваемых изображениях минус единица для получения несмещённой оценки.

Как видно из приведённого выражения для , его структура соответствует структуре выражения (1) и функции влияния (), стоящие в числителе и знаменателе, сокращаются. Таким образом, используемую автокорреляционную функцию можно рассматривать как частный случай отношения (1) и утверждать, что она обладает искомым компенсационным свойством, не требуя при этом введения дополнительной аппаратуры.

Для вычисления двумерной автокорреляционной функции по формуле (2) в кадре, формата точек дискретизации [5 - 7], начиная с первой строки, выделялась полоса шириной 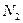пикселя и по центру этой полосы задавался эталон (ЭИ) размером пикселей и записывался в отдельную область памяти БЦОС. Затем эталон, начиная с крайней левой позиции, перемещался по выделенной полосе в текущем изображении (ТИ) с шагом в 1 пиксель. При каждом совмещении эталона и текущего фрагмента полутонового изображения подсчитывался коэффициент корреляции по формуле (2). В связи с тем, что сравниваемые фрагменты и берутся из одного и того же изображения поверхности, то был назван коэффициентом автокорреляции. Найденные значения также сохранялись в памяти БЦОС. Закончив вычисление коэффициентов автокорреляции в первой полосе, задавалась следующая полоса того же формата в исходном изображении, что и предыдущая, но смещённая вниз на один пиксель. В этой полосе по центру задавался новый эталон, но с теми же размерами что и предыдущий, и выполняются те же самые действия для вычисления коэффициента автокорреляции и.т.д. Таким образом, обработав весь кадр исходного изображения по отмеченной методике, в запоминающем устройстве БЦОС формировалась матрица, размерностью 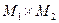коэффициентов автокорреляции или двумерная дискретная автокорреляционная функция. Проведёнными исследованиями в работе [7] было установлено, что по средней амплитуде переменной составляющей автокорреляционной функции исследуемые поверхности с различной шероховатостью существенно отличаются друг от друга при всех указанных размерах эталона. При этом наблюдалось уменьшение этих значений с увеличением размера эталона от 16×16 пикселей до 64×64 пикселя при практически постоянной разнице между исследуемыми микрорельефами. Таким образом, построив аналитическую зависимость = 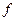() для эталонных образцов с известной шероховатостью можно на основе определения для исследуемой поверхности определять её шероховатость с заданной вероятностью распознавания. Существенным недостатком предложенной методики определения шероховатости на основе вычисления коэффициента корреляции по классической формуле (2) с использованием полутоновых изображений является слишком большое время, затрачиваемое на его вычисление. Так, например, при использовании персональной ЭВМ с процессором Intel(R) Core(TM)2CPU 4300 @ 1.80GHz, время, затрачиваемое на это вычисление, составляет 160000 мс при использовании эталона с форматом 64×64 пикселя. Отмеченное важное обстоятельство практически исключает использование данного метода для оперативного контроля качества поверхности по её шероховатости в производственных условиях.

Для устранения этого основного недостатка в предлагаемой работе были рассмотрены квазиоптимальные алгоритмы для вычисления критериальных функций [13 - 19], к которым и относится рассмотренная выше двумерная автокорреляционная функция. В приведённых работах отмечается, что существующие квазиоптимальные корреляционные алгоритмы были разработаны эвристически, что обусловило различный подход к способам обработки изображений и представлению результатов. Это существенно затрудняет аналитическое исследование существующих алгоритмов и проведение сравнительного анализа при их выборе. Обобщение сведений о квазиоптимальных корреляционных алгоритмах позволяет заметить, что синтез такого алгоритма должен включать следующие этапы:

1) выбор вида предварительной обработки изображения;

2) определение критериальной функции;

3) определение способа поиска экстремума критериальной функции

Применительно к задаче определения микрогеометрии исследуемой поверхности третий этап не является целью и поэтому в дальнейшем не рассматривается.

Полный перечень требований, которым должны удовлетворять критериальные функции, рассмотрен в [15, 16].

Первый этап синтеза квазиоптимального алгоритма основан на том, что с одной стороны, обрабатываемые изображения содержат избыточную информацию, устранение которой при отсутствии помех не влечёт за собой снижение вероятности распознавания неизвестной шероховатости исследуемой поверхности. С другой стороны, сокращение исходной информации посредством снижения информативности изображений является одним из способов уменьшения объёма вычислений при корреляционной обработке. Таким образом, разрабатываемый алгоритм корреляционной обработки во многом определяет и метод предварительной обработки исходного изображения исследуемой поверхности.. Анализ, выполненный в [16, 17], позволил выделить пять групп критериальных функций со сходными свойствами: корреляционные, спектральные, разностные, парные и ранговые.

Разработку квазиоптимального корреляционного алгоритма рассмотрим для определения шероховатости дорожки качения внутреннего кольца приборного подшипника № 2000083 изготовленного из стали ШХ-15, внешний вид которого приведён на рис. 2.

Рис. 2 – Внутреннее кольцо приборного подшипника № 2000083

Схема шлифование дорожки качения цилиндрической поверхности данного кольца на оборудовании Bryant 1-M приведена на рис. 3.

Режим шлифования дорожки был следующий:

частота вращения шпинделя – n_к =1750….1850 об/мин;

коэффициент полезного действия– ή =0,8;

размеры шлифовального круга – D_к =355 мм, В_к =16 мм;

применяемый АК для черновой обработки – 24АМ40СТ1К;

правка круга – поперечная подача S_поп = 0,015 мм /дв.ход, продольная подача S_пр = 0,02 мм/об, минутная подача S_мин= S_пр n_о= 0,02 1850 = 37 мм/мин, алмаз в оправе α= 90⁰, время правки τ=15 с.

Рис. 3 – Схема шлифования дорожки иачения цилиндрической поверхности кольца

В связи с тем, что исследуемое кольцо имеет небольшой радиус наружной окружности – 2,5 мм и ещё меньший радиус поперечного сечения дорожки качения – 0,3 мм, параметры исследовательского оптико-электронного комплекса были настроены таким образом, чтобы уменьшить влияние кривизны исследуемой поверхности на её изображение в фокальной плоскости оптической системы. В данном случае участок анализируемой поверхности имел размер 1,2 1 мм, а формат записываемого в память компьютера изображения составлял 720 576 пикселей. Кроме того, при направлении опорного светового потока перпендикулярно направлению дорожки качения, из-за её сильной кривизны в фокальной плоскости оптической системы наблюдается либо очень сильное светлое пятно при небольших углах падения светового потока ( = 0 – 15 ), либо появление тени от кромки кольца при больших углах падения потока ( >15 ). В связи с выявленными особенностями, опорный световой поток при исследовании шероховатости дорожки качения был направлен вдоль дорожки и под большим углом – = 70 . При такой - же ориентации светового потока были получены изображения поверхностей эталонных образцов формата 720 576 пикселей, приведённых на рис. 4.

=0,13 =0,084 =0,048 =0,025

Рис. 4 – Изображения поверхностей эталонных образцов из стали ШХ – 15 при формате кадра 720 576 пикселей

Шероховатость эталонных образцов определялось традиционными гостовскими методами при помощи профилографа SJ – 201P.

Отметим, что в настоящее время не существует [15, 16] формального способа выбора вида предварительной обработки и типа критериальной функции. В связи с этим синтез квазиоптимальных корреляционных алгоритмов производится эвристически. На основе проведённого анализа для построения двумерных автокорреляционных функций в работе были выбраны парные критериальные функции. Парные критериальные функции предполагают обработку изображений в цифровой форме с числом уровней квантования два и более.

Наибольшее распространение парные критериальные функции получили в системах и алгоритмах, использующих бинарные изображения. При этом наиболее употребляемые парные критериальные функции [18,19] это: функции Рао, Джекарда, Дейка, Соукала и Снита, Кулзинского, Роджерса и Танимото №1 и №2, Соукала и Мишнера, Юла, Хаммана.

С помощью метода парных критериальных функций может быть получено несколько корреляционно – экстремальных алгоритмов. В предлагаемой работе был выбран алгоритм, построенный с использованием парной критериальной функции, в виде

() = ,

где 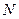– количество сравниваемых элементов в ЭИ и ТИ.

Бинаризация исходного полутонового изображения проводилась по следующему алгоритму. Всё исходное изображение исследуемой поверхности разбивалось на независимые квадратные фрагменты (окна) и в каждом окне подсчитывался средний уровень яркости видеосигнала 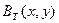. Этот средний уровень и являлся порогом бинарного преобразования для яркости пикселей в данном окне, то есть скользящим порогом [20]. В выделенном окне преобразовывался каждый пиксель, а перемещение окна по преобразуемому изображению осуществляется с шагом, определяемым размерами окна. Отмеченное преобразование использует все три вида фильтрации изображения, то есть каузальную, некаузальную и полукаузальную фильтрации. В результате сравнения каждого байта с пороговым значением ему придавалось новое значение по правилу: = 0FFH, если и = 00H, если < . Такой формат бинарного изображения был выбран для того, чтобы обеспечить возможность его обработки языками высокого уровня и вывода результатов обработки на экран монитора ПЭВМ. На рис.5 приведены бинарные изображения эталонных образцов, полученные при использовании адаптивного окна бинарного преобразования с размерами 16×16 пикселей.

т

=0,13 =0,084 =0,048 =0,025

Рис. 5 – Бинарные изображения поверхностей эталонных образцов

Метод взятия эталона и его последующего перемещения по текущему бинарному изображению для получения автокорреляционной поверхности оставался таким же, как и метод, изложенный выше. Принципиальное отличие нового метода определения двумерной автокорреляционной функции заключается в способе её вычисления по квазиоптимальному корреляционному алгоритму на основе применения парных критериальных функций и , а не по классическому методу с использованием выражения (2).

В этом случае при использовании квазиоптимального корреляционного алгоритма подсчитывается количество совпавших пикселей в текущем фрагменте бинарного изображения и эталоне . Для получения нормированного значения этой суммы она делится на размер эталона, то есть на то значение суммы, которое получается при полном совпадении эталона и текущего фрагмента бинарного изображения. Таким образом, этой нормированной сумме с полным основанием можно придать смысловое значение коэффициента корреляции , так как она отвечает всем требованиям стохастической связи, приведенными в [16, 17], в частности 0 1. При использовании данного метода также компенсируется дополнительная погрешность, возникающая в результате воздействия функции влияния (, ) в связи с тем, что в точке совпадения значений пикселей эталона и выделенного фрагмента текущего бинарного изображения она будет умножаться на ноль, то есть

= (, ) – (, ) =

(, ) ( – ) = (, ) при = .

Кроме того, только в этой точке наращивается отмеченная выше сумма = +1, то есть мера корреляции эталона и текущего фрагмента изображения, согласно алгоритму применения парных критериальных функций и .

Для микрорельефа рассматриваемых поверхностей с помощью оптико-электронного комплекса, в работе были выполнены исследования влияния шероховатости поверхности эталонных образцов на среднюю амплитуду переменной составляющей автокорреляционной функции = 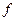(). Результаты выполненных исследований приведены в таблице 1.

Таблица 1 – Зависимость средней амплитуды колебания автокорреляционной функции от шероховатости поверхности при формате изображения поверхности 720 576 пикселей

Шероховатость поверхности образцов
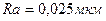
=16,0 =1,7	=12,2 =1,3	=9,9 =0,8	=7,86 =0,1

Для каждого образца также было обработано по 30 изображений с различных участков исследуемой поверхности, то есть = 30 и СКО оценки при определении определялось по формуле [21].

= .

При этом формат эталона и размер окна бинарного преобразования для выполненных исследований составлял 16 16 пикселей.

Следовательно, задавая вероятность распознавания шероховатости исследуемой поверхности 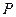=0,99 и = 2,576, для образцов поверхности с = 0,13 мкм имеем = 0,31 мкм, для образцов с = 0,084 мкм имеем = 0,24 мкм, для образцов с =0,048 мкм имеем = 0,15 мкм и для образцов с = 0,025 мкм имеем =0,018 мкм. Используя выражение для доверительного интервала [21]

= ( – ; + )

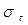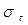получим следующие величины доверительных интервалов:

= 0,13 мкм – = 0,8 отн. ед. 15,2 отн. ед.≤ ≤ 16,8 отн. ед.;

= 0,084 мкм – = 0,6 отн. ед. 11,6 отн. ед.≤ ≤ 12,8 отн. ед.;

= 0,048 мкм – = 0,4 отн. ед. 9,5 отн. ед.≤ ≤ 10,3 отн. ед.;

= 0,025 мкм – = 0,05 отн. ед. 7,81 отн. ед.≤ ≤ 7,91 отн. ед.

График зависимости = для формата изображения исследуемой поверхности 720 576 пикселей приведён на рис. 6.

Рис. 6 – Зависимость доверительного интервала от амплитуды переменной составляющей автокорреляционной функции

Как видно из приведённых данных доверительные интервалы для с увеличением шероховатости возрастают, но не перекрываются, при этом зависимость = имеет нелинейный характер. Используя метод наименьших квадратов, для данного доверительного интервала было получено аналитическое выражение в виде

= (0,09 – 4,2 + 68,5 – 314,9) 10 отн. ед. (3).

На рис.7, согласно данным таблицы 1, приведена зависимость среднего арифметического отклонения профиля поверхности от средней амплитуды переменной составляющей автокорреляционной функции.

Рис.7 – Зависимость 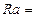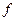() для изображения поверхности с форматом 720 576 пикселей

Согласно приведённому графику, рассматриваемая зависимость 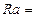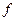() для исследуемых образцов имеет линейный характер и с помощью метода наименьших квадратов может быть представлена в виде

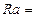0,0013 – 0, 078 мкм (4)

Полутоновые и бинарные изображения типичных участков поверхности дорожки качения внутренних колец приборных подшипников № 2000083 после операции шлифования с применением масляной СОЖ приведены на рис. 8.

№1 №2 №3

Рис. 8 – Изображения дефектных участков дорожек качения внутренних колец приборного подшипника № 2000083 после операции шлифования с применением масляной СОЖ

Ввиду сильной кривизны дорожки качения максимальный формат анализируемых участков поверхности не превосходил значения 450 400 пикселей из общего формата 720 576пикселей, формируемого в памяти компьютера оптико-электронного комплекса. Визуальные исследования дорожек качения с помощью оптико-электронного комплекса показали, что на её поверхности образуются дефекты в виде глубоких рисок и точек, которые встречаются у 95% колец обработанных на шлифовальных станках марки Bryant 1M с применением масляной СОЖ. Риски, как правило, разнонаправленные, что говорит о случайном процессе их образования. Это связано с тем, что масляная СОЖ, подающая в зону обработки, насыщена мелкими осколками абразивных зерен, образующихся после правки шлифовального круга, а также сгустками стружки. Кроме этого на поверхности остаются крупные следы от контактного взаимодействия абразивных зерен с обрабатываемой поверхностью. При шлифовании частицы абразивных зерен после правки и шлама (стружки) не успевают осаждаться в отстойниках, так как масло обладает повышенной вязкостью. Из 30 колец, которые были исследованы, на 27 кольцах обнаружены дефекты (90%).

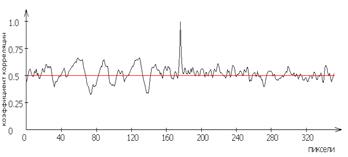
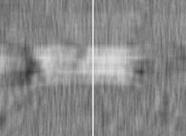
Для рассматриваемых участков поверхности дорожки качения с помощью квазиоптимального корреляционного алгоритма были получены автокорреляционные поверхности, внешний вид которых приведен на рис. 9.

№1

№2

№3

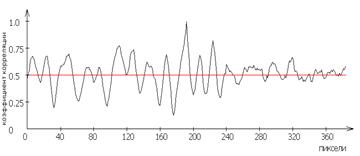
Рис. 9 – Изображения автокорреляционных поверхностей и графиков автокорреляционных функций для участков поверхности дорожки качения приборного подшипника, имеющих дефекты

На этом же рисунке приведены и графики изменения корреляционного сигнала в местах образования отмеченных повреждений дорожки качения.

Анализ приведенных данных показал, что в местах образования повреждений дорожки качения наблюдается возрастание амплитуды переменной составляющей автокорреляционной функции. Измерения этой амплитуды дали следующие значения:

для участка №1 =12,5 отн. ед., для участка №2 =14,34 отн. ед., для участка №3 = 14.3 отн. ед.

Подстановка этих значений в выражения (3) и (4) дала следующие результаты для среднего арифметического отклонения профиля поверхности дорожки качения в повреждённых местах:

участок №1 – = 0,6 отн. ед.; 0,077 , 0,092

участок №2 – = 0,7 отн. ед.; 0,099 , 0,117

участок №3 – =0,69 отн. ед.; 0,098 , 0,116

Дальнейшие исследования применявшегося технологического процесса формирования микрогеометрии дорожки качения внутреннего кольца данного подшипника показали, что последующая операция полирования дорожки качения плохо устраняет образовавшиеся дефекты на этапе шлифования этой дорожки. На рис.10 приведено полутоновое и бинарное изображение участка поверхности дорожки качения этого же подшипника после операции полирования.

Рис. 10 – Полутоновое и бинарное изображения участка поверхности дорожки качения после операции полирования

Полирование дорожки качения колец осуществлялось алмазными пастами зернистостью АСМ 3/2 (алмаз синтетический микропорошок) вручную хлопчатобумажной ниткой диаметром 2 мм. При этом частота вращения кольца подшипника составляла 200 об/мин. Автокорреляционная поверхность и график автокорреляционной функции для рассматриваемой обработки поверхности дорожки качения приведены на рис. 11

Рис. 11 – Изображения автокорреляционной поверхности и графика автокорреляционной функции для поверхности дорожки качения после операции полирования

Средняя амплитуда переменной составляющей автокорреляционной функции для рассматриваемого случая приняла значение = 10,52 отн. ед. Подставляя это значение в формулы (5.3) и (5.4) получили = 0,46 отн. ед.; 0,059 , 0,065 .

Полученные значения среднего арифметического отклонения профиля от средней линии поверхности дорожки качения хоть и стали меньше значений, полученных для поверхности после операции шлифования с применением масляной СОЖ, но всё же не отвечают заданным техническим требованиям. Кроме того, операция полирования оказалась недостаточно эффективной, т.к. остались следы повреждения поверхности дорожки качения от предыдущей её обработки путём шлифования, как это хорошо видно на рис. 12.

&

Дата добавления: 2015-07-11