Лінзи Френеля

Лінзи Френеля - оптичні елементи зі східчастим профілем поверхні. Вони виявляються дуже корисними в сенсорах і датчиках, де висока якість фокусування не потрібна. Основне застосування в сенсорах знаходять світлові конденсатори, лупи, і фокусуючі елементи.

Френелівскі лінзи можуть бути виготовлені зі скла, акрилу (видимий і близький інфрачервоний діапазон), або поліетилену (далекий інфрачервоний діапазон). Історія Френелівських лінз почалася в 1748, коли Кант Буфон запропонував шліфувати тверді частини скляної лінзи сходами концентричних зон, щоб зменшувати товщину лінзи й звести до мінімуму втрату енергії. Він зрозумів, що тільки поверхня лінзи необхідна, щоб заломити світло, оскільки, як тільки світло усередині лінзи, воно поширюється далі по прямій лінії. Його ідея була змінена в 1822 Огастином Фреснелом (1788-1827). Він створив лінзу, у якій центри кривизни різних кілець зменшувалися із віддаленням від центру, щоб фактично усунути сферичні аберації. Концепція такої лінзи представлена на Рис. 4.13, де зображена звичайна плоско-опукла лінза. Лінза розділена на кілька концентричних кілець. Після зрізання всіх кілець лінза ще залишиться лінзою, яка заломлює падаючі промені в загальний фокус, який задається Рів. (4.24). Зміна кута відбувається коли промені, що виходять, залишають криву поверхню. Кільцеві секції, відзначені буквою x, не вносять вклад у фокусуючі властивість. Якщо всі такі секції вилучені, лінза має вигляд, показаний на Рис. 4.13B, і буде повністю зберігати свої властивості фокусування світлових променів. Тепер усі кільця можуть бути зміщені по відношенню один до друга, щоб вирівняти їхні плоскі поверхні (Рис. 4.13C). Результуюча майже плоска лінза називається Френелівською, яка має майже ті ж самі властивості фокусування, як і оригінальна плоско-опукла лінза. Френелівська лінза в основному складається з ряду концентричних призматичних заглиблень, призначених для колективного фокусування падаючих променів світла в загальний фокус.

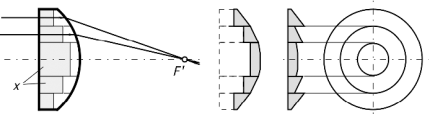
(A) (C) (B)

Рис. 4.13. Принцип дії Френелівської лінзи.

Френелівська лінза має ряд переваг у порівнянні зі звичайною лінзою – невелика вага, товщина, може бути вигнута (у випадку пластмасової лінзи) до будь-якої бажаної форми, і, що найбільш важливо, має більш низькі втрати на поглинання світлового потоку. Остання особливість дуже важлива для виготовлення лінз середнього й далекого інфрачервоного діапазону, де поглинання в матеріалі може бути суттєвим. Із цієї причини в датчиках руху використовується майже винятково полімерні Френелівські лінзи для далекої інфрачервоної області.

Зазвичай виготовляються два типи Френелівських лінз. Один - лінза з постійним кроком (Рис. 4.14A), а інший – лінза з постійною глибиною (Рис. 4.14B). На практиці, важко підтримати кривизну поверхні кожним маленьким заглибленням; отже, профіль заглиблення апроксимується плоскою поверхнею. Це означає, що сходи розміщені близько один до одного. Фактично, чим менше крок, тим більш точна лінза.

У лінзі з постійним кроком, кут нахилу φ кожного заглиблення - функція його відстані h від оптичної осі. У результаті, глибина сходів збільшуються з відстанню від центру. Центральна частина лінзи може бути плоска, якщо її діаметр - принаймні, в 20 раз менше, ніж фокальна довжина.

(A) (B)

Рис. 4.14. Френелівська лінза з постійним кроком (А) і з постійною глибиною (B).

Для короткофокусних лінз - бажано підтримувати сферичний профіль центральної частини. Кут нахилу кожного кроку може бути визначений з наступної формули, яка вірна при маленьких величинах h:

φ =arctan[hn/f (n-1)], (4.28)

де f - фокальна довжина.

Для лінз із постійною глибиною, і похилий кут φ і величина кроку r змінюються з відстанню від центру. Наступні рівняння можуть бути корисні для розрахунків лінзи. Відстань від центру заглиблення може бути знайдена через номер ξ заглиблення (передбачається, що центральна частина має номер 0);

h = √2f (n-1)ξd - ξ² d², (4.29)

і кут нахилу

φ =arcsin[h/(n-1)f ]. (4.30)

Загальна кількість заглиблень у лінзі може бути знайдене через Френелівську апертуру лінзи D (максимальний розмір):

Г = {(n-1)f - √[f ² (n-1) ² -D²]}/d. (4.31)

Френелівська лінза може бути злегка вигнута, якщо це вимагає конструкція датчика. Однак вигин змінює положення фокальних точок. Якщо лінза зігнута її заглибленнями усередину викривлення, фокусна відстань зменшується.

Рис. 4.15. Порівняння сферичних і асферических профілів лінзи.

Відомо, що сферична поверхня лінзи дає сферичні аберації.

Тому, для застосувань, де потрібна високоякісне фокусування, безперервна поверхня, контури заглиблень якої задані, не повинні бути сферичні, а асферичні. Профіль безперервної асферичної поверхні може описуватися стандартним рівнянням конічних, аксиально-симетричних щодо осі z лінз (Рис. 4.15):

Z =CY²/[1 +√1- (K +1) C²Y²], (4.32)

де Z і Y - координати поверхні, C – верхня точка кривизни, і K - конічна постійна. Вершина скривлення й конічна постійна може бути обрана залежно від бажаних характеристик лінзи й контур кожного заглиблення може бути визначений, використовуючи це рівняння. C і K будуть залежати від декількох факторів, типу бажаної лінзи, її фокусної відстані, індекса заломлення, і конкретного застосування.

Дата добавления: 2015-07-11