Радіометрія

Давайте розглянемо проходження світла через тришаровий матеріал. Усі шари зроблені з різних матеріалів названих середовищами. На Рис. 4.2 показано, що відбувається із променем світла, який проходить через плоскі пластини з першого середовища в друге середовище, і потім у третє. Частина падаючого світла відбивається від плоскої границі між першим й другим середовищами згідно із законом відбиття, який історично приписують Евклиду:

Θ₁ =Θ΄₁ (4.1)

Частина світла входить у пластину (середовище 2) під іншим кутом. Новий кут Θ₂

визначається відповідно до закону заломлення, який був відкритий в 1621 г. Снеллиусом В. (1580-1626) і відомий як закон Снеллиуса:

n₁ sinΘ₁ =n₂ sinΘ₂, (4.2)

Де n₁ і n₂ - показники заломлення двох середовищ.

У будь-якому середовищі, світло поширюється більш повільно, ніж у вакуумі. Коефіцієнт заломлення є відношення швидкості світла у вакуумі, c₀, і в середовищі, c:

n = c₀ / c, (4.3)

Рис. 4.2. Проходження світла через середовища з різними коефіцієнтами заломлення

Оскільки c < c₀ індекс заломлення середовища завжди більший за одиницю.

Швидкість світла в середовищі безпосередньо визначається діелектричної постійної ε_r середовища, яка також визначає заломлюючий індекс:

n=√ ε_r (4.4)

Рис. 4.3. Характеристики прозорості для різних оптичних матеріалів.

Взагалі, n - функція довжини хвилі. Залежність від довжини хвилі індексу заломлення проявляється в призмі, яка використовувалася Сером Исааком Ньютоном у його експериментах зі спектром світла. У видимому діапазоні, індекс заломлення n часто вказується на довжині хвилі 0.58756 мкм, жовтогарячої лінії гелію. Індекси заломлення для деяких матеріалів представлені в Табл. 19 у Додатку.

Залежність коефіцієнта заломлення від довжин хвилі називається дисперсією. Зміна n з довжиною хвилі звичайно дуже повільне й часто незначне, якщо тільки довжина хвилі не наближається до області, де матеріал не прозорий. На Рис. 4.3 показані криві прозорості деяких оптичних матеріалів.

Частина світла, відбитого від границі під кутом Θ΄₁, залежить від швидкостей світла у двох суміжних середовищах. Кількість відбитого потоку Ф_ρ пов'язане з падаючим потоком Ф ₀ через коефіцієнт відбиття, який може бути виражений за допомогою заломлюючого індексу:

ρ = Ф_ρ /Ф₀=[(n₁ - n₂)/(n₁ +n₂)]² (4.5)

Рівняння (3.139) і (4.5) указують на те, що й відбиття й поглинання залежать винятково від заломлюючого індексу матеріалу на конкретній довжині хвилі.

Якщо світловий потік надходить із повітря в об'єкт, що має заломлюючий індекс n, Рів. (4.5) спрощується:

ρ =[(n - 1)/(n +1)] ² (4.6)

Рис. 4.4. Світло, що проходить через оптичну пластину.

Перед виходом променя із другого середовища (Рис. 4.2) і входом у третє середовище із заломлюючим індексом n₃, інша частина цього променя відбивається усередину від другої границі розділу середовищ із n₂ і n₃ під кутом Θ΄₂. Інша частина променів виходить під кутом Θ₃, який також визначається згідно із законом Снелліуса. Якщо середовища 1 і 3 - ті ж самі (наприклад, повітря) по обидві сторони пластини, тоді n₁ = n₃ і Θ₁ = Θ₃. Цей випадок ілюструє Рис. 4.4.

Як випливає з Рів. 4.5, коефіцієнти відбиття ті ж самі для світла відбитого від границі поділу й світла, яке надходить у середовище з меншим або більшим індексом заломлення.

Загальний коефіцієнт двох відбиттів від обох поверхонь пластини може бути знайдений зі спрощеної формули:

ρ₂ ≈ ρ₁ (2 - ρ₁), (4.7)

де ρ₁ - коефіцієнт відбиття від першої поверхні. У дійсності, відбите світло від другої границі знову відбивається від першої границі назад до другої границі, і так далі. Таким чином, уважаючи, що немає ніякого поглинання в матеріалі, повні втрати на відбиття в межах пластини можуть бути розраховані через заломлюючий індекс матеріалу:

ρ₂ = 1- 2n/(n² +1). (4.8)

Відбиття збільшується при збільшенні різниці в заломлюючих індексах. Наприклад, якщо видиме світло поширюється без поглинання з повітря в пластину з важкого кварцового скла, два відбиття приводять до втрат приблизно рівних 11%, а те ж саме для повітря-германій-повітря (у далекому інфрачервоному спектральному діапазоні), втрати на відбиття рівні приблизно 59 %. Для зменшення втрат в оптичних матеріалах часто застосовують анти відбивні покриття, які мають індекси заломлення й відповідні товщини для певних довжин хвиль.

Тоді баланс випромінювання у Рів. (3.134) повинен бути змінений, щоб включити два відбиття в оптичному матеріалі:

ρ₂ +α +γ =1, (4.9)

де α є коефіцієнтом поглинання й γ є коефіцієнтом пропускання. В області прозорості α ≈ 0, і тоді пропускання:

γ =1 – ρ₂ ≈ 2n/(n² +1). (4.10)

Рівняння (4.10) визначає теоретично можливий максимум пропускання оптичної пластини. У вищезгаданому прикладі пропускання скляної пластини - 88.6 % (видимий діапазон), у той час як пропускання германієвої пластини - 41 % (далека ІЧ область). У видимому діапазоні пропускання германія є нульовим. Це означає, що 100 % світла відбивається й поглинається. На Рис. 4.5 показане відбиття й поглинання тонкої пластини як функції коефіцієнтів заломлення. Тут, пластина - будь-яке оптичне обладнання (наприклад, вікно або лінза), яке використовується в межах її спектрального діапазону, (тобто, там, де її втрати на поглинання незначні (α ≈ 0)).

На Рис. 4.6 показаний розподіл енергії в межах оптичної пластини, коли світловий потік Ф₀ падає на її поверхню. Частина падаючого потоку відбивається - Ф_ρ, інша частина, Ф_α - поглинається матеріалом, і третя частина, Ф_γ, пропускається матеріалом.

Поглинута частина світла перетвориться в теплову енергію, частина якої ΔР губиться на підтримку стану пластини і її оточення за допомогою теплової провідності й конвекції.

Інша частина поглинутого світла піднімає температуру матеріалу пластини. Збільшення температури може мати місце, наприклад, коли матеріал використовується як вікно в потужному лазері. Інший приклад, збільшення температури може заподіяти проблеми для датчиків інфрачервоної області. Проблема пов'язана з потоком Ф_ε = Ф_α - ΔP, який

випромінюється матеріалом через його температурну зміну. Це називається вторинною радіацією. Природно, що випромінюваний спектр залежить від температури матеріалу й, як правило, розташований у далекій інфрачервоній області спектра. Спектральний розподіл

вторинної радіації відповідає розподілу поглинаючої здатності матеріалу, тому що поглинаюча й випромінююча здатність – фактично те ж саме.

Рис. 4.5. Відбиття й пропускання тонкої пластини як функції заломлюючого індексу.

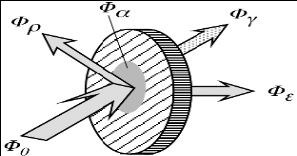
Рис. 4.6. Розподіл світлової енергії в оптичній пластині.

Для матеріалів з низьким поглинанням, коефіцієнт поглинання може бути визначений через підвищення температури матеріалу:

α = mc/Ф_γ·2n/(n² +1)·(dT_g/dt + dT_L/dt)·T₀, (4.11)

де m і c - маса й питома теплоємність оптичного матеріалу, відповідно, T_g і T_L - нахили ділянок кривої підвищення й зниження температури матеріалу, відповідно, при температурі випробувань T₀. Строго говорячи, світло в матеріалі губиться не тільки через поглинання, але також через розсіювання. Загальні втрати в матеріалі залежать від його товщини й можуть бути виражені через так званий коефіцієнт ослаблення g і товщину зразка h. Коефіцієнт пропускання може бути визначено з Рів. (4.10), яке змінено для розрахунків ослаблення:

γ≈ (1-ρ₂)·e^-gh. (4.12)

Коефіцієнт ослаблення (або загасання) g звичайно визначається виготовлювачами

оптичних матеріалів.

Дата добавления: 2015-07-11