Задачи и упражнения

1. Какое множество точек на плоскости определяет уравнение х ² + у ² –
– 4 х + 10 у + 29 = 0?

2. Найти координаты центра и радиус окружности, определяемой уравнением х ² – 6 х + у ² + 12 у + 36 = 0.

3. Записать каноническое уравнение эллипса, проходящего через точки .

4. Найти фокусы и эксцентриситет эллипса 3 х ² + 4 у ² = 12.

5. Какую линию определяет уравнение 9 х ² – 4 у ² = 36. Найти фокусы и эксцентриситет.

6. Найти полуоси, координаты фокусов и эксцентриситет гиперболы, заданной уравнением 5 х ² – 4 у ² = 20.

7. Записать уравнение асимптот и директрис гиперболы 4 х ² – 9 у ² = 36.

8. Большая ось эллипса равна 12, а директрисами его служат прямые
х = ±18. Составить уравнение эллипса.

9. Найти полуоси, составить уравнения асимптот и директрис гиперболы 3 х ² – 4 у ² = 12.

10. Найти координаты фокуса и уравнение директрисы параболы у ² = 8 х.

11. Найти координаты фокуса и уравнение директрисы параболы х ² = 4 у. Вычислить расстояние от точки М (6; 9) до фокуса.

12. Составить уравнение гиперболы, зная, что расстояние между ее директрисами равно 4, а расстояние между фокусами 16.

13. Найти координаты фокусов, эксцентриситет, уравнения асимптот
и директрис гиперболы 9 х ² – 16 у ² = 144.

14. Найти координаты фокуса и уравнение директрисы параболы у ² = 12 х. определить расстояние от точки М (3; 6) до фокуса.

15. Записать матрицу квадратичной формы j (х ₁, х ₂, x ₃) = .

16. Определить знакоопределенность квадратичных форм.

а) j (х ₁, х ₂, x ₃) = ,
б) j (х ₁, х ₂, x ₃) = .

ОТВЕТЫ

1. Точка М (2; -5).

2. М (3; -6), R = 3.

3.

4. F ₁ (-1; 0), F ₂ (1; 0), e = 0,5.

5.

6. а = 2, в = , F ₁ (-3; 0), F ₂ (3; 0), e = 1,5.

7.

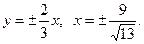
8.

9. а = 2, в = ,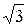

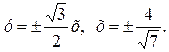
10. F (2; 0), х = -2.

11. F (0; 2), у = -2, r = 10.

12.

13. F ₁ (-5; 0), F ₂ (5; 0), e = ,

14. F (3; 0), х = -3, r = 6.

15.

16. а) положительно определена,
б) квадратичная форма не является знакоопределенной.

ЛИТЕРАТУРА

1. Гусак А. А. Аналитическая геометрия и линейная алгебра.– Мн.: Тетрасистемс, 1998.

2. Овсеец М. И., Светлая Е. М. Сборник задач по высшей математике. Учебное издание.– Мн.: ЧИУиП, 2006.– 67 с.

СОДЕРЖАНИЕ

Лекция 1. КРИВЫЕ ВТОРОГО ПОРЯДКА..................................... 3

1. Окружность. Эллипс.................................................................... 3

2. Гипербола..................................................................................... 6

3. Парабола...................................................................................... 9

Лекция 2. КВАДРАТИЧНЫЕ ФОРМЫ........................................... 14

1. Понятие квадратичной формы и способы ее записи................... 15

2. Знакоопределенность квадратичных форм. Критерии положительной и отрицательной определенностей............................................................. 16

Задачи и упражнения........................................................................... 20

Ответы.................................................................................................. 21

Литература...................................................................................... 21

c d

Учебное издание

Дата добавления: 2015-07-10