Решение. Пусть М (х, у). Тогда çMNú = 2 çMFú , çMNú = ç–4 – xú

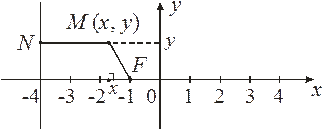
Пусть М (х, у). Тогда ç MN ú = 2 ç MF ú , ç MN ú = ç–4 – x ú , ç MF ú = = 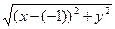, Þ ç– (4 + х)ú = .

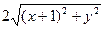Возведем в квадрат: (4 + х)² = 4 ((х + 1)² + у ²),

Þ 16 + 8 х + х ² = (х ² + 2 х + 1 + у ²) · 4 = 4 х ² + 8 х + 4 + 4 у ²,

Þ 3 х ² + 4 у ² = 12 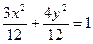Þ Þ .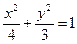

Таким образом, точка М (х, у) движется по эллипсу.

ПРИМЕР 4.

Написать уравнение гиперболы, имеющей вершины в фокусах, а фокусы – в вершинах эллипса .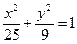

Дата добавления: 2015-07-10