ЗАДАНИЕ № 21

Для плоской волны справедливо утверждение …

ВАРИАНТЫ ОТВЕТОВ:

1. Амплитуда волны не зависит от расстояния до источника колебаний (при условии, что поглощением среды можно пренебречь).

2. Амплитуда волны обратно пропорциональна расстоянию до источника колебаний (в непоглощающей среде).

3. Волновые поверхности имеют вид концентрических сфер.

---------------------------

Указания к заданиям № 16 -21

Уравнение плоской гармонической волны, распространяющейся вдоль оси ОХ:

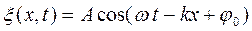, где

x(x,t) – смещение частицы среды, находящейся на расстоянии х от источника колебаний в момент времени t;

A – амплитуда колебаний;

w – круговая (циклическая) частота;

k – волновое число;

;

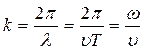l – длина волны;

υ – скорость распространения волны ();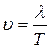

Т – период колебаний;

j₀ – начальная фаза колебаний.

Уравнение сферической гармонической волны:

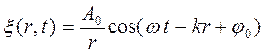, где

r – расстояние от точечного источника колебаний до рассматриваемой точки среды на сферической поверхности радиуса r.

Дата добавления: 2015-07-11