ЗАДАНИЕ № 5

Частица может колебаться вдоль оси x под действием результирующей силы с амплитудой А и частотой w, где k – положительная константа. В момент, когда x=А/ 2, скорость частицы будет равна:

ВАРИАНТЫ ОТВЕТОВ:

1) ; 2) ; 3) ;

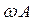4) ; 5) .

---------------------------

Указания к заданиям № 1 – 5

Гармонические колебания величины (координаты материальной точки) описываются уравнением:

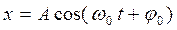, где

А – амплитуда колебаний – максимальное значение колеблющейся величины;

ω₀ – круговая (циклическая) частота;

– фаза колебаний в момент времени t;

j₀ – начальная фаза колебаний.

Скорость материальной точки: .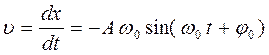

Ускорение материальной точки: .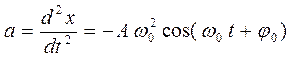

Максимальные значения смещения x, скорости u, ускорения a:

Дата добавления: 2015-07-11