Краткие теоретические сведения.

Изменения токов и напряжений, вызванные подключением независимых источников к цепи или их отключением называют переходными колебаниями, а сам процесс - переходным. При этом считается, что подключение и отключение (коммутация) источников происходит мгновенно.

В цепях, содержащих энергоемкие элементы, переходный процесс, как правило, длится определенное время. Это обусловлено тем, что изменение геометрии цепи или параметров элементов обычно влечет за собой изменение запаса энергии полей индуктивностей и емкостей. Электрическое и магнитное поля, имея материальную структуру, обладают инерцией. Следовательно, для изменения запаса их энергии необходимо время.

В резистивных электрических цепях энергия не запасается, поэтому переходные процессы в них происходят мгновенно вслед за произведенной коммутацией.

Частным случаем переходных колебаний являются колебания при отключении источников от цепи. Эти колебания осуществляются под действием энергии полей реактивных элементов, если они есть в цепи. В цепи в этом случае отсутствуют какие-либо источники, и цепь предоставлена самой себе. Поэтому колебания в цепи, происходящие после отключения от нее источников, называют свободными.

В цепи с потерями в процессе свободных колебаний токи и напряжения в цепи стремятся к нулю по мере преобразования энергии полей реактивных элементов в тепло или другие виды энергии.

Для оценки поведения цепи в переходном и свободном режимах пользуются понятиями переходной и импульсной характеристик.

Переходной характеристикой 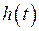называется отношение реакции цепи на ступенчатое воздействие при нулевых начальных условиях к высоте ступенчатого воздействия.

Воздействие будем обозначать 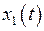, а соответствующую ему реакцию - . Тогда ступенчатое воздействи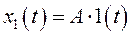е , где - высота ступенчатого воздействия, - единичная ступенчатая функция, а переходная характеристика

. (3.1)

В зависимости от размерностей и может быть безразмерной и размерной. Если, например, воздействием является источник напряжения, то для реакции в виде напряжения на некоторой ветви будет безразмерной, а для реакции в виде тока в ветви будет измеряться в сименсах. При воздействии в виде источника тока переходная характеристика будет либо безразмерной, либо измеряться в омах. Нетрудно видеть, что переходная характеристика численно равна реакции цепи на единичное ступенчатое воздействие, но размерность переходной характеристики не совпадает с размерностью реакции.

Другой важнейшей характеристикой является импульсная характеристика цепи. Определим её.

Пусть воздействием на цепь при нулевых начальных условиях является , где - единичная импульсная функция, - площадь импульсного воздействия. Пусть реакцией, соответствующей этому воздействию, является . Тогда импульсная характеристика цепи 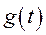по определению есть

. (3.2)

Численно импульсная характеристика равна реакции на 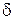-функцию, хотя здесь также возникает проблема размерности.

Связь между переходной и импульсной характеристиками определяется следующими выражениями:

, (3.3)

. (3.4)

Из формулы (3.3) следует, что в зависимости от вида воздействующего источника (напряжения или тока) и реакции (напряжение или ток) импульсная характеристика может измеряться в различных единицах (, , ).

Импульсная и переходная характеристики называются временными характеристиками цепи.

Для физически реализуемой цепи:

,

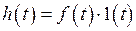где - некоторая непрерывная функция. В связи с этим нужно обратить внимание на технику дифференцирования при применении формулы (3.3):

.

Второе слагаемое всюду равно нулю за исключением точки . Поэтому

. (3.5)

Обратим внимание ещё на один важный момент. Импульсная функция, воздействующая на цепь, мгновенно вносит в неё запас энергии. Этот факт можно понять посредством предельного перехода, взяв в качестве воздействия прямоугольный импульс единичной площади и устремив длительность воздействия к нулю. Фактически энергия вносится за время длительности импульса.

Отсюда понятно, что для реакции в виде напряжения на ёмкости или тока в индуктивности в импульсной характеристике будут наблюдаться скачки при . Это не является нарушением законов коммутации. Для импульсная характеристика всегда представляет собой сводный процесс.

Рассмотрим пример нахождения временных характеристик для RL - цепи, изображённой на рис.3.1. Воздействием является источник . В качестве реакций возьмём и . Соответствующие временные характеристики обозначим , .

Сначала положим . Это соответствует включению постоянной э.д.с. при в цепи при нулевых начальных условиях. Для

,

.

Разделив эти реакции на и учтя, что для , получим:

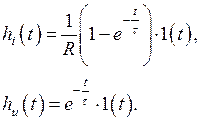
Обратим внимание, что измеряется в сименсах, а безразмерна, что и должно быть при воздействии в виде э.д.с.

Импульсные характеристики найдём как производные от переходных, воспользовавшись формулой (3.5):

С другой стороны, для RC-контура (рис.3.2, а) переходное напряжение на емкости при подключении его к источнику постоянного напряжения определяется выражением

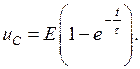(3.6)

Временная диаграмма этой зависимости приведена на рис.3.2, б. Переходная характеристика относительно этой реакции

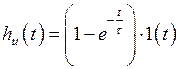. (3.7)

Теоретически переходный процесс длится бесконечно долго. На примере изменения напряжения на емкости нетрудно убедиться, что скорость переходного процесса зависит от постоянной времени . Действительно,

(3.8)

Чем больше , тем медленнее нарастает напряжение, и наоборот. Если в уравнении (3.8) положить , то получим угловой коэффициент касательной к кривой при . Уравнение касательной имеет вид

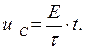
Точка пересечения касательной и прямой соответствует . Следовательно, постоянную времени можно найти как подкасательную к кривой . Построения, необходимые для графического определения , приведены на рис.3.2, б.

Если в выражение (3.6) подставить , то получим . Это означает, что постоянную времени можно рассматривать как промежуток времени, по истечении которого напряжение на емкости нарастает до 63,2% от установившегося значения.

Если в том же выражении положить , то получим , т.е. по истечении времени напряжение на емкости отличается от установившегося значения не более чем на 5%. Следовательно, по истечении времени можно считать, что переходный процесс практически завершился.

Экспериментальное исследование переходных и свободных колебаний осуществляется при использовании генератора прямоугольных импульсов (ГПИ) и осциллографа. При этом для исследования свободных колебаний (импульсных характеристик) длительность импульсов на выходе ГПИ необходимо выбрать значительно меньше длительности свободных колебаний. Эти импульсы, играя роль импульсной функции, на экране осциллографа практически не наблюдаются, но в то же время достаточны для обеспечения начальных зарядов емкостей и начальных токов индуктивностей. Период следования импульсов должен быть больше длительности собственных колебаний токов и напряжений.

При исследовании переходных характеристик длительность прямоугольных импульсов, передний фронт которых играет роль ступенчатой функции, должна быть больше длительности переходного процесса.

Дата добавления: 2015-09-04