Правило де моргана

Структуры систем без восстановления описываются при помощи булевых функций. Одним из важных правил работы с булевыми функциями является известное в математической логике прави­ло де Моргана. Прежде чем перейти к нему, напомним закон двойного отрицания, который гласит, что

Правило де Моргана гласит:

Это правило становится очевидным, если взглянуть на цепоч­ку диаграмм Венна (рис. 2.3).

Тождество (2.12) легко доказать с использованием диаграмм Венна

(рис. 2.4).

Используя закон двойного отрицания, можно получить экви­валентное выражение:

Действительно,

Очевидно, этот же результат легко получается и с использова­нием диаграмм Венна.

Нетрудно аналогичным образом получить еще две эквивалент­ные формы:

Далее, легко обобщить это правило во всех его четырех формах на любое число переменных:

Покажем принцип получения этих формул на примере форму­лы (2.17) для трех переменных, используя правило де Моргана и закон двойного отрицания:

§ 2.4. ПАРАЛЛЕЛЬНАЯ СИСТЕМА — ГОРЯЧИЙ РЕЗЕРВ

Параллельной называется система, которая сохраняет свою рабо­тоспособность до тех пор, пока работоспособен хотя бы один ее эле­мент. Предполагается, что все элементы находятся во включенном со­стоянии с самого начала.

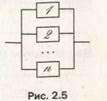
В инженерной практике такой резерв называют нагруженным или горячим. Параллельная система, состоящая из п элементов, описывается при помощи следующей блок-схемы надежности, представленной на рис. 2.5.

В каждый момент времени функции системы выполняются ос­новным элементом, а в случае его отказа происходит мгновенное переключение на любой из исправных к данному моменту резерв­ных элементов.

Булева функция, удовлетворяющая этому требо­ванию, имеет вид

или

Воспользовавшись правилом де Моргана, можно записать удобное выражение для структурной функции параллельной системы:

из которого следует выражение для ВБР в виде

Формула (2.25) имеет простое физическое объяснение: систе­ма отказывает при отказе всех ее элементов, а ВБР находится как вероятность дополнительного события.

Отметим следующие свойства параллельной системы:

ü с увеличением числа элементов системы ее надежность при прочих равных условиях повышается;

ü надежность системы в целом всегда выше, чем надежность любого из ее элементов (в том числе и наилучшего).

Обычно параллельные системы состоят из идентичных эле­ментов. Это и естественно, так как элементы, замещающие друг друга, должны быть одинаковыми. В этом случае

Если элементы системы имеют идентичное экспоненциальное распределение времени до отказа (см. Приложение 2) и являются высоконадежными, т. е. q(t) << 1, то можно записать приближен­ную формулу:

Иначе говоря, для малых t распределение момента появления отказа параллельной системы хорошо приближается распределени­ем Вейбулла — Гнеденко с параметрами а = А. и р = п (см. П 2.12).

Среднее время безотказной работы параллельной системы в об­щем случае можно найти лишь путем численного интегрирования.

В случае экспоненциального распределения и идентичных элементов интегрирование функции вероятности безотказной ра­боты не вызывает затруднений. Действительно, используя (2.27), можно записать:

Введя новую переменную у = 1 - exp(-λt), можно записать

или окончательно

Следует отметить, что среднее время безотказной работы па­раллельной системы с нагруженным резервом растет довольно медленно с ростом числа резервных элементов. В табл. 2.1 приве­ден расчет для экспоненциального распределения, которое, кста­ти, дает еще относительно большой рост по сравнению с боль­шинством стареющих распределений.

В то же время мы видим, что такой вид резервирования очень эффективен для повышения ВБР.

§2.5. СИСТЕМА ТИПА «k ИЗ п»

Система типа «k из n» состоит из п элементов, и для ее работоспо­собности нужно, чтобы не менее k из них были бы работоспособны. Структурная функция такой системы может быть записана в виде

Наиболее часто встречается на практике система типа «2 из 3». Для такой системы структурная функция записывается как

Здесь члены логической суммы записаны в скобках лишь для удобства прочтения. Из(2.31)следует, что

Таблица 2.1

Число элементов в параллельной системе	Относительный рост среднего времени работы системы
	2.88
	5.18
	6.48

В общем случае система «k из п» соответствует биномиальной схеме испытаний (см. Приложение 2), т. е. можно записать ее ВБР в виде

Для высоконадежных систем, когда q<<1/n, имеет место просто приближенное выражение

(2.34)

Если элементы имеют экспоненциальное распределение вре­мени работы до отказа, то среднее время безотказной работы сис­темы типа «k из n» находится по аналогии с (2.30) в виде

В общем случае приходится находить Т_сист, интегрируя (2.33) численными методами.

Заметим, что когда k = п, система типа «к из п» превращается в обычную

последовательную систему Ф(х) = П x_i = min x_p (2.36)

а когда k = 1 - в параллельную систему:

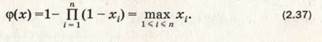
2.6. СИСТЕМЫ СО СМЕШАННОЙ СТРУКТУРОЙ

2.6.1. Параллельно-последовательные

и последовательно-параллельные структуры

Системы с чисто последовательной или чисто параллельной структурой встречаются на практике довольно редко. Чаще при­ходится иметь дело со смешанными структурами: с параллель­но-последовательными системами (параллельное соединение после­довательных подсистем) и с последовательно-параллельными систе­мами (последовательное соединение параллельных подсистем), представленными на рис. 2.6, а также их комбинациями.

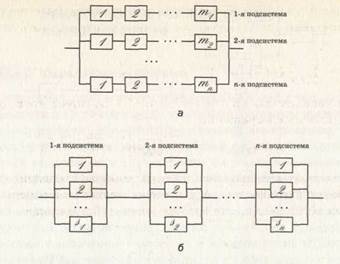
Рис. 2.6

Для параллельно-последовательной структуры, представлен­ной на рис. 2.6, а, ВБР записывается как

где m_j — число элементов в j-й группе последовательно соединен­ных элементов, а для последовательно-параллельной структуры (рис. 2.6, б) имеем

здесь s _j — число элементов в j-й группе параллельно соединен­ных элементов.

2.6.2. Общий случай приводимых структур

В общем случае системы имеют гораздо более сложные смешан­ные структуры. Однако они почти всегда редуцируются до более простых систем, т. е. являются приводимыми структурами. По­яснить это удобнее всего с помощью конкретного примера. Рас­смотрим смешанную структуру (рис. 2.7) и проведем с ней про­цедуру редукции блок-схемы надежности.

Рис. 2.7

Сначала выделим две подсистемы: последовательную из элемен­тов 2 и 3 и параллельную из элементов 4 и 5, преобразовав эти фраг­менты в соответствующие эквивалентные элементы 6 и 7. Затем элементы 6 и 7 преобразовываются в эквивалентный элемент 8. Наконец, вся система сводится к последнему эквивалентному эле­менту 9.

Построение выражения для вероятности безотказной работы системы начнем с конца. Ясно, что Р_сист = р₉. Далее, р₉ = р₁р₈. Подставляя р₈ = 1 - q₆q₇, получаем р₉ =р₁(1 - q₆q₇). Подставляя

р₆₌ ргрз и p₇ = 1 - q₄q₅ получаем р ₉ = р₁ (1 – (1- p₂p₃)q₄q₅), где искомое Р_сист выражено через вероятность безотказной работы «атомарных» элементов.

Кроме приводимых структур, имеются также неприводимые структуры, которые будут рассмотрены в главе 3.

§ 2.7. НЕНАГРУЖЕННОЕ РЕЗЕРВИРОВАНИЕ — ХОЛОДНЫЙ РЕЗЕРВ

2.7.1. Параллельная система

Уже отмечалось, что горячее резервирование является достаточно неэффективным с точки зрения увеличения среднего времени рабо­ты до отказа. Более эффективным является ненагруженное, или хо­лодное, резервирование, когда на рабочей позиции находится един­ственный элемент, но в случае отказа он мгновенно заменяется на новый исправный элемент. Конечно, нужно понимать, что подобная схема мгновенной замены является идеализированной: практически подключение нового элемента требует определенного разогрева: в сильноточных электрических схемах это связано с переходными процессами в источниках питания, в механических объектах — с инерционностью подвижных деталей, а в цифровых — с необходи­мостью загрузки программ и повторного ввода входных данных.

Для случая холодного резерва условная блок-схема надеж­ности представлена на рис. 2.8.

Рассмотрим систему, состоящую из п элементов, из которых основной находится в рабочем режиме, а остальные (п - 1) — в хо­лодном. Естественно предполагать, что при такой схеме резерви­рования все элементы системы идентичны. Также предполагает­ся, что, находясь в резерве, элементы не теряют своих качеств и не могут отказать. Случайное время работы системы Х_сяст можно записать через соответствующие наработки отдельных элементов:

Для среднего времени работы системы до отказа имеем

T_сист = nT (2.41)

Заметим, что выражение (2.41) справедливо для любых распределений времени до отказа элемен­тов. Распределение времени работы до отказа у та­кой системы определяется как распределение сум­мы случайных величин, т. е. выражается через n-кратную свертку:

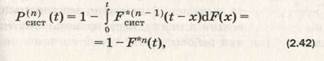где F*ⁿ(t) обозначает n-кратную свертку. По определению n-кратная свертка рекуррентно определяется как

Формула (2.42) дает простое выражение в случае экспоненциальности распределения времени работы до отказа элемента. В этом случае время работы системы представляет собой сумму п экспо­ненциальных случайных величин с одним и тем же параметром λ.

Что означает, что рассматриваемая система не откажет за вре­мя t?

Это означает, что с вероятностью e ^-λt не произойдет ни одного отказа, с вероятностью λ te ^-λtпроизойдет ровно один отказ, с вероят­ностью e ^-λt произойдет ровно два отказа, и так далее до

(n - 1) отказов. Иначе говоря, ВБР такой системы записывается в виде

Формула (2.43) задает распределение Пуассона (см. Прило­жение 2).

Из (2.43) можно получить удобную приближенную формулу

для вероятности Р'"' (t) безотказной работы в случае высокона­дежной системы, т. е. при

λt <<1/n:

2.7.2.

Система типа «k из n»

Система этого типа обладает резервированием более общего типа, чем предыдущая: здесь постоянно включено k элементов, а (я - k)

находятся в режиме ожидания. Блок-схему надежности в этом случае будем изображать в виде, представленном на рис. 2.9.

Как только возникает (п — k + 1)-й от­каз, система в целом отказывает. Если распределение времени до отказа элемен­та экспоненциальное, то получить выра­жение для среднего времени безотказной работы и ВБР такой системы не составляет труда. Заметим, что до момента появления (п — k + 1)-го отказа поток отказов такой системы является пуассоновским с параметром X_k, а следовательно:

Из (2.46) следует приближенная формула для высоконадежной системы:

При произвольных распределениях времени работы до отказа элементов общие выражения абсолютно неконструктивны и обыч­но приходится использовать численные методы, включая метод Монте-Карло.

---

Дата добавления: 2015-09-04