К определению ширины спектра широкополосного сигнала

Аннотация. В статье рассматривается понятие ширины спектра узкополосного сигнала и приводится способ определения ширины спектра для сложных ширикополосных сигналов с помощью моментов четвертого порядка

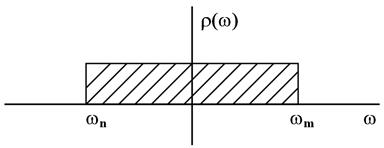
Узкополосным мы называем сигналы, спектр которых сосредоточен вблизи какой-то опорной частоты ω₀. У широкополосных сигналов, напротив нет разницы между спектральной плотностью вблизи ω=0 и вблизи ее максимума

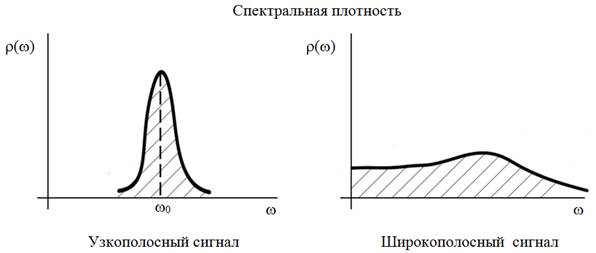
Ширина спектра W – понятие математически несколько размытое, определенное с сущности только по порядку величины. Для широкополосного сигнала можно все-таки придерживаться простой формулы:

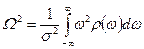
где, как и далее, введена ­мгновенная дисперсия

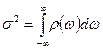
И подразумевается, что выписанные интегралы существуют. Момент же четвертого порядка можно использовать для определения индекса концентрации по образцу так называемого эксцесса [1]:

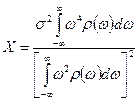
В частности, при равномерной спектральной плотности r(ω) = r₀ в интервале –ω_n<ω<ω_m имеем

Легко доказывается, что оценка Х является минимальной для всех плотностей r(ω), убывающих от нулевого значения ω к периферии. Действительно, при этом условии

,

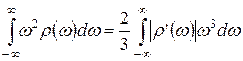
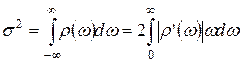и остается применить неравенство Буняковского [2]

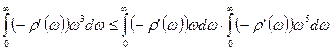
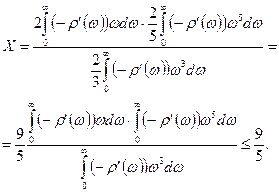
Заметим, что при нарушении условия монотонности r(w) нижняя граница для l отодвигается до Х=1 (в силу того же неравенства Буяковского), но значения Х в интервале 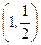типичны для узкополосных, а не для широкополосных сигналов.

Вообще же для узкополосных сигналов положение сложнее. Если под ω₀ подразумевается значение частоты, более или менее близкое к среднему арифметическому

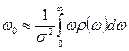, то

,

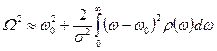Т.е. главной частью W² оказывается не собственно ширина спектра, выраженная последним интегралом, а квадрат средней частоты.

Для исправления этого недостатка применением интегральное определение, включающее момент четвертой степени

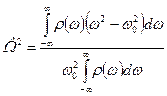(1)

Величина 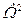, действительно, характеризует собственно ширину спектра (при мало-мальски разумном определении ω₀)

Список литературы

1. Рытов С.М. Введение в статистическую радиофизику. Случайные процессы. М.: Наука, 1976, 495с.

2. Ахиезер Н.И. Лекции по теории аппроксимации, Гостехиздат, 1947, стр.12.

Дата добавления: 2015-09-04