Логическое индексирование

Логическая индексация заключается в задании некоторого условия выбора элементов из массива.

Например, если требуется сформировать логический вектор той же длины, что и вектор y, в котором логическая единица соответствует элементам вектора y меньшим пяти, а логический ноль соответствует элементам вектора y большим или равным пяти, то следует записать логическое выражение для массива y с использованием операции сравнения (знака меньше <):

>> y=[1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9];

>> index = y<5

index =

Columns 1 through 8

1 1 1 1 1 1 1 1

Columns 9 through 16

0 0 0 0 0 0 0 0

Columns 17 through 18

0 0

Если требуется определить элементы, превосходящие, например, в полтора раза среднее значение всех элементов 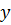, то достаточно применить логическое индексирование и функцию mean:

>> index=y>1.5*mean(y)

index =

Columns 1 through 8

0 0 0 0 0 0 0 0

Columns 9 through 16

0 0 0 0 0 0 1 1

Columns 17 through 18

1 1

Как обычно для операций сравнения применяются знаки == (два знака = для логического "равно"), >, >=, <, <= и ~= ("не равно").

Для задания более сложных условий требуется применять логические операции, которые приведены в следующей таблице в порядке убывания приоритета (для изменения порядка выполнения логических операции используются круглые скобки). Логические операции имеют также и функциональную форму записи, т.е., например, следующие логические выражения

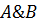и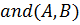

приведут к одинаковому результату.

Логические операции
Операция	Обозначение	Функциональная запись
отрицание	~A	not(A)
логическое И	A&B	and(A,B)
логическое ИЛИ	A | B	or(A,B)

Здесь A и B - логические массивы, полученные, например, в результате применения операций сравнения к массивам, как в предыдущем примере. К соответствующим элементам массивов A и B поэлементно применяются обычные логические операции, и результатом является логический массив.

Если мы хотим для приведенного выше массива 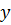сформировать логический массив, в котором логические единицы отвечают элементам массива 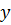, лежащим от трех до шести, то для этого подойдет следующее логическое выражение:

>> A = y>=3

A =

Columns 1 through 10

0 0 0 0 1 1 1 1 1 1

Columns 11 through 18

1 1 1 1 1 1 1 1

>> B = y<=6

B =

Columns 1 through 10

1 1 1 1 1 1 1 1 1 1

Columns 11 through 18

1 1 0 0 0 0 0 0

>> index = A&B

index =

Columns 1 through 10

0 0 0 0 1 1 1 1 1 1

Columns 11 through 18

1 1 0 0 0 0 0 0

Можно, разумеется, было обойтись и без вспомогательных массивов A и B и записать одно выражение:

>> index = (y>=3) & (y<=6)

index =

Columns 1 through 10

0 0 0 0 1 1 1 1 1 1

Columns 11 through 18

1 1 0 0 0 0 0 0

Операции сравнения имеют больший приоритет, чем логические операции, поэтому можно было обойтись и без скобок, т.е. записать

>> index = y>=3 & y<=6

однако, выражение со скобками более наглядно.

Приведем еще один пример, в котором задан массив 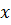(значения независимой переменная) и 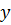( 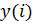- значения зависимой переменной в x 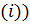, и требуется сформировать логический массив, в котором логические единицы соответствуют тем элементам массива 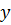, которые лежат в полосе, ограниченной двумя линиям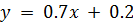и

и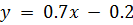

>> x=0:0.2:3;

>> y=2*sin(x);

>> index = (y<=0.7*x+0.2) & (y>=0.7*x-0.2)

index =

Columns 1 through 10

1 0 0 0 0 0 0 0 0 0

Columns 11 through 16

0 1 0 0 0 0

Дата добавления: 2015-09-04