Гидродинамика неньютоновских жидкостей

Ньютоновскими называются жидкости, движение которых подчиняется закону внутреннего трения Ньютона. Вязкость этих жидкостей остаетсяпостоянной при данных температуре и давлении.

В отличие от них вязкость неньютоновских жидкостей не постоянна, а изменяется в зависимости от скорости сдвига, его продолжительности.

В технологии строительных материалов к таким жидкостям относятся цементные шламы, растворы, бетонные смеси, растворы полимеров, лакокрасочные материалы и др.

Неньютоновские жидкости делят на три класса.

К первому классу относятся вязкие (стационарные) жидкости, для которых функция P = f(dw/dx) не зависит от длительности действия сил сдвига.

К этому классу относятся следующие жидкости:

· Бингамовские;

· Псевдопластические;

· Дилатантные.

Течение бингамовской жидкости (реологическая модель, которой приведена на рис. 9) начинается только после приложения напряжения сдвига Р₀ ≥ Р, которое необходимо для разрушения структуры, образовавшейся в данной системе.

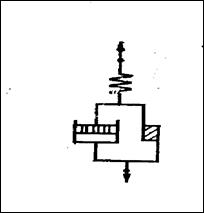
Рис. 9. Модель вязкопластичного тела Бингама

Такое течение называется пластическим, а критическое (т.е. предельное) напряжение сдвига Р₀ – пределом текучести.

При напряжениях, меньших Р₀, бингамовские жидкости ведут себя, как твердые тела, а при напряжениях, больших Р₀ – как ньютоновские жидкости, т.е. зависимость P = f(dw/dx) является линейной. Считается, что структура тела Бингама под действием предельного напряжения сдвига мгновенно и полностью разрушается, в результате чего тело Бингама превращается в жидкость, при снижении напряжения структура восстанавливается и тело возвращается к твердому состоянию.

Уравнение кривой течения бингамовской жидкости называется уравнением Шведова-Бингама:

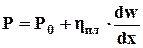(26)

где η_пл – пластическая вязкость (коэффициент жесткости).

Для большинства структурированных систем зависимость P = f(dw/dx) выражается не прямой, а представляет кривую (рис. 10).

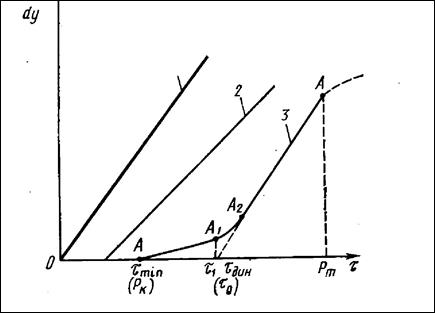
Рис. 10. Кривая течения бингамовской жидкости

Различают два предельных напряжения сдвига:

· нижний предел текучести Р_к – статическое предельное напряжение сдвига, величина которого соответствует началу остаточной деформации (отрезок ОА, т.А – предел упругости);

· динамическое предельное напряжение сдвига Р_о = Р_дин, соответствующее уравнению Шведова-Бингама.

Кривую течения структурированной системы можно условно разделить на 4 области, характеризующие состояние системы в процессе нагружения.

Область А-А₁ – практически прямая линия, в которой пластическое течение системы происходит без заметного разрушения структуры при наибольшей пластической вязкости (шведовской), имеющей постоянное значение:

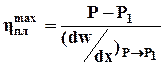(27)

Нарушение структуры в этой области столь незначительно, что успевает восстановиться в процессе течения.

Область А₁-А₂ –область пластического течения с постоянным разрушением структуры. Пластическая вязкость резко падает, вследствие чего скорость течения быстро увеличивается.

Область А₂-А₃ – область предельно разрушенной структуры, выше которой течение происходит с наименьшей пластической вязкостью (бингамовской):

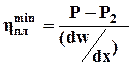(28)

Переход к этой области характеризуется динамическим предельным напряжением сдвига Р₀. Дальнейшее увеличение напряжений системы завершается разрывом сплошности структуры, характеризующейся пределом прочности Р_max.

К псевдопластическим жидкостям относятся суспензии с ассиметричными или волокнистыми частицами твердой фазы, а также растворы многих высокополимеров, целлюлозы.

Псевдопластические жидкости начинают течь уже при самых малых значениях напряжения сдвига. Течение этих жидкостей характеризуется тем, что их вязкость зависит от градиента скорости. Поэтому для псевдопластических жидкостей говорят о кажущейся вязкости, которая представляет собой отношение напряжения сдвига к градиенту скорости.

С увеличением скорости сдвига кажущаяся вязкость этих жидкостей уменьшается.

Для таких жидкостей в соответствии с уравнением Оствальда напряжение сдвига определяется соотношением:

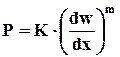(29)

где K и m – постоянные коэффициенты (m < 1)

Коэффициент К зависит от консистенции жидкости и увеличивается с ростом вязкости. Коэффициент m характеризует степень неньютоновского поведения жидкости, и чем больше m, тем ближе жидкость по характеру течения к ньютоновской.

При бесконечно большом градиенте скорости кривая течения постоянна и переходит в прямую с предельным значением кажущейся вязкости, равным бесконечности (рис. 11).

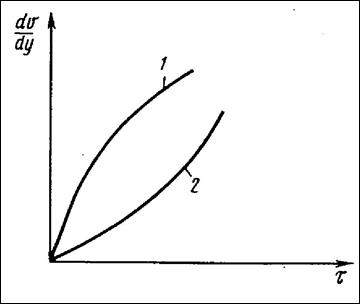
Рис. 11. Кривые течения псевдопластической 1 и дилатантной 2 жидкостей

К дилатантным жидкостям относятся суспензии с большим содержанием твердой фазы. В таких жидкостях, находящихся в состоянии покоя, жидкость удерживается в прослойках между частицами. При небольших скоростях деформации она служит смазкой.

Эти жидкости характеризуются возрастанием кажущейся вязкости с увеличением градиента скорости.

Течение этих жидкостей также описывается уравнением Оствальда, но при m > 1.

Ко второму классу относятся неньютоновские жидкости, характеристики которых зависят от времени (нестационарные жидкости).

Эти жидкости характеризуются тем, что их кажущаяся вязкость зависит не только от скорости сдвига, но и от продолжительности действия сдвигового усилия.

Если жидкость деформируется с постоянной скоростью, то напряжение сдвига во времени может нарастать или убывать. В зависимости от этого различают два вида жидкости:

· тиксотропные;

· реопектические.

В тиксотропных жидкостях с увеличением продолжительности воздействия постоянного напряжения сдвига структура разрушается и текучесть возрастает (рис. 12).

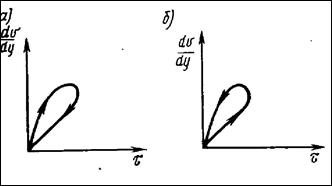
Рис. 12. Кривые течения тиксотропных а и реопектических жидкостей б.

После снятия напряжения структура может самопроизвольно восстанавливаться, т.е. тиксотропия является обратимым процессом.

К тиксотропным жидкостям относятся многие краски, строительные растворы, бетонные смеси, керамические массы. Именно благодаря тиксотропным свойствам краски легко удерживаются на вертикальной стене, не стекая.

Реопектические жидкости характеризуются ростом структурообразования при увеличении скорости сдвига и продолжительности воздействия напряжения сдвига (рис. 12).

К таким жидкостям относятся многие коллоидные растворы, суспензия гипса в воде.

Установлено, что при больших скоростях сдвига у этих жидкостей наблюдается не образование, а разрушение структуры.

К третьему классу относятся вязкоупругие или максвелловские жидкости.

Эти жидкости текут под действием напряжения сдвига, но после снятия напряжения они частично восстанавливают свою структуру. Таким образом, эти жидкости обладают двойным свойством: вязким течением по закону Ньютона и упругим восстановлением формы по закону Гука.

По классификации П.А. Ребиндера жидкости по пластично-вязким свойствам делятся на:

· нормально-вязкие (ньютоновские);

· аномально-вязкие (псевдопластические, дилатантные, реопектические и тиксотропные);

· пластичные (бингамовские).

Первые две системы П.А. Ребиндер объединяет в одну группу – жидкообразные системы, а последнюю называет твердообразной системой.

Изменение вязкости в зависимости от напряжения сдвига для жидкообразных систем представлено на рис. 13.

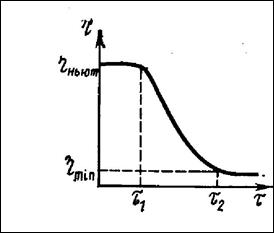
Рис. 13. Кривая течения жидкообразной системы

Для них при напряжениях, меньших Р₁, вязкость имеет наибольшую величину, равную ньютоновской вязкости практически не разрушенной структуры. При напряжениях, свыше Р₁, вязкость уменьшается до предельного значения η_min.

Изменение вязкости в зависимости от напряжения сдвига для твердообразных систем представлено на рис. 14.

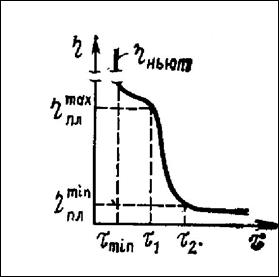
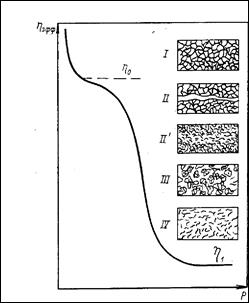
Рис. 14. Кривая течения твердообразной системы

При напряжениях сдвига, меньших P_min, максимальная вязкость η₀ (ньютоновская вязкость) не разрушенной структуры бесконечно велика. При этом происходит деформация структурной сетки без разрушения или с тиксотропным восстановлением структуры в потоке (область I).

При дальнейшем повышении напряжения сдвига до Р_т проявляется наибольшая пластическая вязкость η^*_max. Здесь появляются разрывы сплошности (области II и II^’).

При повышении напряжения сдвига в области постоянного разрушения структуры (до Р₂) пластическая вязкость постоянно уменьшается до η^*_min. Имеет место распад структуры на агрегаты, размер которых уменьшается, а число увеличивается в процессе сдвиговой деформации (область III).

Дальнейшее течение осуществляется с вязкостью предельно разрушенной структуры.

Дата добавления: 2015-09-02