Геометрический способ решения системы линейных неравенств.

Предположим, что в каждом уравнении системы

(1)

хотя бы один из коэффициентов при неизвестных х и у отличен от нуля. Тогда любое из этих двух уравнений можно рассматривать как уравнение прямой в прямоугольной системе координат. Действительно, возьмем, например, первое уравнение

a ₁ x + b ₁ y = c ₁.

Если b ₁ =/= 0, то уравнение можно переписать в виде:

Это уже знакомое нам уравнение прямой (см. § 3).

При b ₁ = 0 уравнение a ₁ x + b ₁ y = c ₁принимает вид a ₁ x = c ₁, или

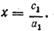
Это соотношение можно рассматривать как уравнение прямой, параллельной оси у и пересекающей ось х в точке с абсциссой c ₁/ a ₁ (смотри, например, рисунок 41, на котором представлены прямые х = — 1 и х = 2).

Поэтому результаты, полученные в предыдущих параграфах, допускают простую геометрическую интерпретацию.

С системой уравнений (1) свяжем две прямые: прямую a ₁ x + b ₁ y = c ₁ и прямую a ₂ x + b ₂ y = c ₂ (рис. 42).

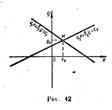
Если эти прямые имеют общую точку М, то координаты ее (х ₀, у ₀) определяют некоторое решение системы уравнений (1).

Обратно: каждое решение системы уравнений (1) можно рассматривать как координаты точки, принадлежащей одновременно и прямой a ₁ x + b ₁ y = c ₁ и прямой a ₂ x + b ₂ y = c ₂. Таким образом, система уравнений (1) имеет столько решений, сколько общих точек содержат прямые a ₁ x + b ₁ y = c ₁ и a ₂ x + b ₂ y = c ₂.

Любые две прямые либо имеют одну общую точку (пересекающиеся прямые), либо не имеют ни одной общей точки (параллельные прямые), либо имеют бесконечно много общих точек (сливающиеся друг с другом прямые). Соответственно этому система уравнений (1) либо имеет единственное решение (случай 1), либо несовместна, то есть не имеет ни одного решения (случай 2), либо имеет бесконечно много решений (случай 3). Поясним это на трех частных примерах.

Примеры. 1. Системе уравнений

соответствуют прямые, представленные на рисунке 43. Они пересекаются в одной точке с координатами

Следовательно, данная система имеет единственное решение х = 2, у = 1.

2. Системе уравнений

соответствуют параллельные прямые.

Они не пересекаются ни в одной точке. Данная система уравнений несовместна.

3. Для системы уравнений

соответствующие прямые сливаются в одну прямую линию (рис. 45).

О такиx прямых можно сказать, что они пересекаются в бесконечном множестве точек, а именно в каждой своей точке. Поэтому данная система уравнений имеет бесконечное множество решений. Все эти решения можно представить как координаты точек, лежащих на этой прямой. Если х принять за t, то для у получим у = 1 — 2 t.

Дата добавления: 2015-09-02