Метод экстраполирования по экспоненте

Математическая модель по этому методу имеет вид экспоненциальной функции:

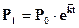, (7.10)

где: e – основание натурального логарифма (2,7183);

Применение экспоненциальной функции более предпочтительно по сравнению с линейной функцией и степенной, т.к. это гарантирует, что численность населения не станет отрицательной.

Используя этот метод, можно рассчитать период удвоения численности населения и среднегодовой коэффициент прироста населения.

Период удвоениянаселения получаем путём следующих преобразований исходной формулы (7.10):

, (7.11)

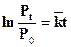(7.12)

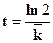(7.13)

Соответственно, период сокращения населения вдвое будет тогда рассчитываться по следующей формуле:

(7.14)

Задание 7.2. Известно, что население одного из регионов России имеет среднегодовой темп сокращения, равный 1,41% (данные условные).

Требуется определить число лет, через которое постоянное население уменьшится в 2 раза.

Решение:

Период сокращения населения вдвое рассчитаем по формуле 7.14:

(лет).

Среднегодовой коэффициент прироста населения можно определить путём преобразований промежуточной формулы расчёта (7.12):

(7.15)

(7.16)

Б. Аналитический метод – основан на подборе функции, наиболее близкой по своему графическому отображению к эмпирической кривой.

Например, часто применяется логистическая функция ("логистик" с греческого – искусство вычислять, рассуждать), особенность которой в демографическом прогнозировании состоит в том, что её приращение уменьшается по мере роста численности населения.

Дата добавления: 2015-09-01