Природные арки

.

Расчёт арок

Иногда природные арочные образования служат в качестве реальных конструкций, так как по ним могут быть проложены действующие дороги. Примеры подобных арок можно найти в природных парках Carter Caves State Resort Park и Natural Bridge State Resort Park в Кентукки.

Согласно классификации Национального парка Арки (штат Юта, США), каменный проём должен иметь ширину не менее 3 футов (0,914 метра) и располагаться в достаточно большой стене, чтобы считаться аркой. При этом арки через естественные водотоки, а также через пересохшие русла, называются природными мостами. Отверстия в скалах, расположенные достаточно далеко от краёв и не влияющие на форму скалы, арками не считаются^[3].

В основе расчёта арочных конструкций лежит расчёт кривого стержня, элемента отличного от прямой балки, у него ось представляет собой тот или иной тип кривой линии (ось — линия, проходящая через центры тяжести поперечных сечений элемента). С допустимым приближением касательные напряжения от поперечной силы для кривых стержней можно определять по той же формуле Журавского, что и для прямых балок^[1]:

,

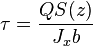где

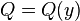• — поперечная сила, действующая на балку ( 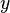— продольная координата),
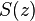• — статический момент отсеченной площади сечения на расстоянии 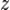относительно нейтральной оси,
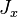• — момент инерции всего сечения элемента относительно центральной оси 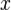, перпендикулярной плоскости арки,
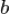• — ширина сечения элемента на расстоянии 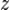от нейтральной оси.

Соответственно, условие прочности по касательным напряжениям для кривых стержней будет представляться следующим образом^[1]:

.

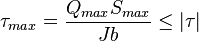Напряжения в кривом стержне, вызываемые нормальной силой, нормальны к сечению и равномерно распределены по его площади, то есть^[1]:

,

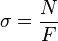где

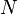• — нормальная сила, действующая на элемент
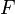• — площадь сечения элемента.

Гиперболический закон распределения нормальных напряжений в криволинейном стержне от действия момента

Изгибающий момент, как и в прямой балке, вызывает в кривом стержне только нормальные напряжения. Распределение их по высоте сечения определяется следующей формулой^[1]:

,

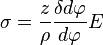где

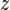• — расстояние от нейтральной оси до точки, где определяется напряжение
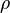• — радиус кривизны в точке
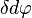• — величина изменения угла между смежными сечениями под действием момента
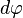• — начальный угол между сечениями
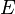• — Модуль Юнга.

Получается, что в отличие от прямой балки, где напряжения распределяются по линейному закону, в криволинейном стержне нормальные напряжения от момента распределяются по гиперболическому закону. Из этого следует несколько важных выводов, а именно: при изгибе кривого стержня нейтральная ось не проходит через центр тяжести сечения; напряжения в наружных волокнах элемента меньше, чем при таком же изгибе прямой балки, а во внутренних волокнах — больше; рост напряжений по высоте сечения происходит с разной скоростью. Наибольшей величины напряжения достигают с внутренней стороны. Однако они достаточно быстро убывают по глубине. Если конструкция работает в статическом режиме и сделана из пластичных материалов, не подверженных хрупкому разрушению, то перенапряжения на самом краю сечения с внутренней стороны могут не представлять опасности^[1].

Формула нормальных напряжений от момента будет иметь вид^[1]:

,

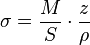а формула полных нормальных напряжений в кривом стержне^[1]:

.

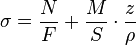Радиус кривизны нейтрального слоя определяется из уравнения^[1]:

.

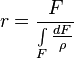Из формул следует, что чем меньше отношение радиуса кривизны стержня к высоте его сечения, тем больше работа кривого стержня отличается от работы прямой балки. Когда же радиус оси намного превосходит размеры сечения, работа кривого стержня похожа на работу прямой балки и нормальные напряжения в этих случаях будут почти равны. Чаще всего арки в строительных конструкциях относятся ко второй категории кривых стержней. К первой же можно отнести разнообразные криволинейные детали: крюки, звенья цепей, колец и пр^[1].

Деформации, возникающие в кривых стержнях, в общем случае определяются следующими выражениями^[1]:

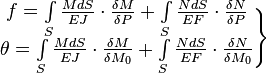
где

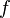• — линейное перемещение центра тяжести сечения
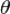• — угол поворота сечения.

В большинстве случаев, однако, влиянием кривизны для определения деформаций можно пренебречь^[1].

Купол

Разрез купола Пантеона

Ку́пол (итал. cupola — купол, свод, от лат. cupula, уменьшительное от cupa — бочка)^[1] — пространственная несущая конструкция покрытия, по форме близкая к полусфере или другой поверхности вращения кривой (эллипса, параболы и т. п.). Купольные конструкции перекрывают преимущественно круглые, многоугольные, эллиптические в плане помещения и позволяют перекрывать значительные пространства без дополнительных промежуточных опор. Образующими формами служат различные кривые, выпуклые вверх. От вертикальной нагрузки в купольных конструкциях возникают усилия сжатия, а также горизонтальный распор на опорах.

Дата добавления: 2015-09-01