Two methods of calculating the characteristics of the strip dielectric waveguide

УДК 621.396

Г.С. Малышев, А.Ю. Седаков, А.А. Титаренко

Нижегородский государственный технический университет им. Р.Е. Алексеева

Два метода расчёта характеристик полоскового диэлектрического волновода

Сравниваются два метода расчёта дисперсионных характеристик открытого прямоугольного диэлектрического волновода. Рассматривается вопрос корректности применения лучевого метода к расчёту полосковых диэлектрических волноводов в широком диапазоне частот.

Ключевые слова: модифицированный метод Галёркина, лучевой метод, открытый диэлектрический волновод, полосковый волновод

G. S. Malishev, A. A. Titarenko, A. Yu. Sedakov

Nizhny Novgorod State Technical University named R.Y. Alekseev

Two methods of calculating the characteristics of the strip dielectric waveguide

The article compares two methods for calculating the dispersion characteristics of open dielectric waveguide. The article deals with the question of the correctness of the application of the ray method for calculation of strip waveguides in a wide range of frequencies.

Keywords: modified Galerkin method, ray method, open dielectric waveguide, strip waveguide

Открытые диэлектрические волноводы (ОДВ) и устройства на их основе находят широкое применение в технике СВЧ и оптического диапазонов волн. В работе [1] был предложен спектральный метод анализа открытых диэлектрических волноводов, основанный на методе интеграла Фурье [2] и модифицированном методе Галеркина [3]. Изложим основные положения указанного метода.

Рассмотрим ОДВ с произвольным поперечным сечением (рис. 1):

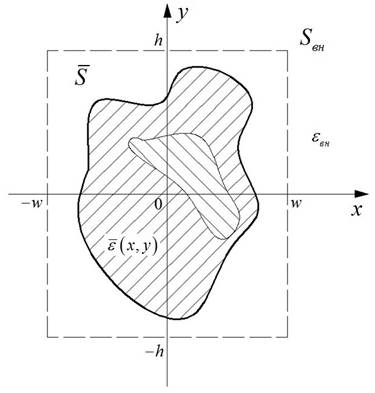
Рис. 1. ОДВ с произвольным поперечным сечением

Функция, задающая значение диэлектрической проницаемости в каждой точке сечения, определяется следующим образом:

то есть в пределах поперечного сечения ОДВ (внутри пунктирного контура, рис. 1) диэлектрическая проницаемость задаётся функцией , в окружающем пространстве диэлектрическая проницаемость имеет постоянную величину (область вне пунктирного контура).

Компоненты электрического поля в такой структуре должны удовлетворять уравнениям Максвелла, скалярная форма записи которых имеет вид

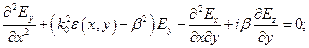(1)

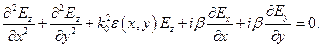
Решения системы уравнений (1) представим в виде интегралов Фурье [2]:

;

; (2)

.

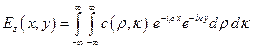Особенность представления полей в виде (2) состоит в том, что компоненты электрического поля записываются независимо друг от друга со спектральными коэффициентами , и 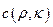. Для установления связи между последними, а значит, между компонентам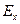и , и , подставляем выражения (2) в систему (1), в результате чего получаем:

(3)

Используя равенства

, ,

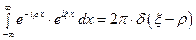где 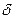- дельта-функция Дирака, произведем над записанной системой двумерное преобразование Фурье, то есть каждое уравнение системы (3) умножим на и проинтегрируем по переменным x и y в пределах от до . В результате получаем систему трех однородных интегральных уравнений Фредгольма 2-го рода относительно амплитудных функций , и 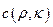из представления Фурье (2):

(4)

При решении этой системы неизвестные функции , и 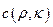будем искать в виде разложений [3] по полиномам Эрмита с весовыми функциями:

;

; (5)

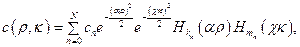
где 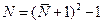, а индексы и определяются как , , 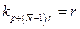, . и - это масштабирующие коэффициенты, подбирая которые мы можем влиять на скорость сходимости представлений (5). При проведении расчётов полагаем, что 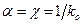, где 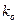- волновое число свободного пространства, которое вычисляется один раз для какой-нибудь одной частоты.

Подставляем (5) в систему (4). Умножаем каждое из уравнений поочерёдно на функции

,

и интегрируем по переменным и в пределах от до . Используя соотношения ортогональности [4] полиномов Эрмита с весовыми функциями

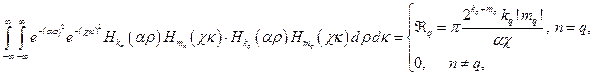
получаем СЛАУ относительно неизвестных коэффициентов разложения , 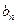и , :

где - ненормированное продольное волновое число. Матрица системы имеет размерность . Приравнивая её определитель нулю, получаем дисперсионное уравнение волн ОДВ. Элементы матриц K, I, , J, и W, каждая из которых имеет размерность , определяются формулами, приведёнными в работе [1]. Важно отметить, что все эти элементы (за исключением элементов матрицы W) не зависят ни от параметров диэлектрического волновода, ни от частоты. Их значения определяются только номером приближения, что позволяет рассчитывать их (в заданном приближении) один раз, заносить в компьютерную память и далее просто считывать их. Это позволяет принципиально сократить время счета.

Для расчёта дисперсионных характеристик полоскового волновода (рис. 2) можно [5] использовать лучевой метод. Метод является приближённым. Достоинством его является возможность получить дисперсионные уравнения исключительно простой структуры. Скорость вычисления корней таких дисперсионных уравнений существенно возрастает, что имеет большой практический интерес. Именно поэтому важно проверить состоятельность лучевого подхода при описании полоскового волновода, в особенности в нижней части частотного диапазона.

Рис. 2. Геометрические размеры поперечного сечения полоскового волновода

Опишем процедуру поиска корней дисперсионных уравнений, полученных с помощью лучевого подхода [5]. С точки зрения лучевого метода полосковый волновод представляется как суперпозиция двух симметричных плёночных волноводов, один из которых имеет толщину плёнки w, а другой – h. В одном из этих волноводов распространяется (рис. 3) волна типа H, в другом – волна типа E. В результате в полосковом волноводе образуются гибридные волны HE и EH. Для расчёта дисперсионных характеристик гибридных волн полоскового волновода необходимо сначала найти корни дисперсионных уравнений для плёночных волноводов с толщиной w и h.

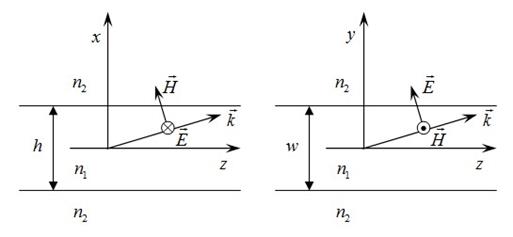
Рис. 3. Две плоские волны, суперпозиция которых даёт 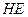волну

В качестве примера рассмотрим алгоритм расчёта дисперсионной характеристики волны 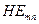с чётным индексом m и нечётным индексом n. Ориентацию осей x и y выбираем так, как показано на рис. 3. На фиксированной частоте находим корни дисперсионного уравнения волны симметричного слоя с толщиной h

, , , (6)

где - это нормированное на 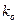продольное волновое число, и - это нормированные на 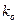поперечные волновые числа в полоске и оболочке, соответственно. Уравнение (6) записано для случая чётных m (волнам с чётными и нечётными индексами соответствуют разные дисперсионные уравнения).

Затем находим корни дисперсионного уравнения волны 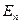симметричного слоя с толщиной w (индекс n - нечётный)

, , .

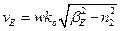Определив и , мы находим соответствующие им значения и 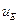, которые подставляем в формулу, связывающую волновые числа:

,

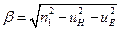где - нормированное на 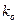продольное волновое число волны 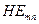с чётным индексом m и нечётным индексом n.

Рис. 4. Дисперсионные характеристики первых пяти волн полоскового волновода

На рис.4 приведён результат расчёта дисперсионных характеристик первых пяти волн полоскового волновода. Расчёт производился двумя методами – спектральным (полагалось, что ) и лучевым. Из рис. 4 видно, что два метода дают хорошее совпадение только в области высоких частот. В приближении к критическим частотам расхождение увеличивается.

Для численной оценки расхождения, даваемого двумя методами, воспользуемся выражением:

,

где и - коэффициенты замедления, рассчитанные спектральным и лучевым методами, соответственно, - коэффициент замедления основной волны, рассчитанный спектральным методом. Зависимость параметра 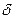от частоты для первых пяти волн полоскового волновода (рис. 4) представлена на рис. 5.

Рис. 5. Относительная разность между коэффициентами замедления для волн, дисперсионные характеристики которых показаны на рис. 4

Из рис. 5 видно, что погрешность лучевого метода возрастает с увеличением номера волны. Различия связаны с тем, что в приближении лучевой модели плоские волны, образующие поле, рассматриваются попарно независимо. При этом не учитывается взаимодействие плоских волн взаимно ортогональной поляризации. Тем не менее, для каждого конкретного типа волн на высоких частотах оба метода дают хорошее совпадение.

Для основной волны в области низких частот сравниваемые методы дают не только количественное, но также и качественное отличие. Это связано с тем, что на низких частотах перестаёт выполняться условие применимости лучевого подхода: .

Таким образом, за исключением низкочастотной области лучевой метод при расчёте полосковых световодов даёт вполне достоверные результаты. В СВЧ диапазоне целесообразно использовать волновой подход.

Литература

[1] Раевский, С.Б. Расчет открытых продольно регулярных диэлектрических волноводов с произвольным поперечно неоднородным сечением / С.Б. Раевский, А.А. Титаренко // Радиотехника и электроника. – 2009. – №11. - С.1285-1299.

[2] Сотская, Л.И. Метод интегрального уравнения в теории слабонаправляющих неоднородных оптических волноводов / Л.И. Сотская, А.Б. Сотский // ЖТФ. – 2002. – т.72. – №12ю – С.1-8.

[3] Раевский, С.Б., Метод электродинамического расчета прямоугольных закрытых волноводов с произвольным диэлектрическим заполнением / С.Б. Раевский, А.А. Титаренко // Антенны. – 2007. – вып. 2 (117). – С.4-11.

[4] Градштейн, И.С. Таблицы интегралов, сумм, рядов и произведений / И.С. Градштейн, И.М. Рыжик. – М.: Физматгиз, 1963. – 1100с.

[5] Унгер, Х. Г. Планарные и волоконные оптические волноводы / Х.Г. Унгер. – М.: Мир, 1980. - 656с.

Дата добавления: 2015-09-05