Примеры решения задач. Пример 1. Определить количество информации, связанное с появлением каждого символа в

Пример 1. Определить количество информации, связанное с появлением каждого символа в сообщениях, записанных на русском языке.

Решение:

Возьмем русский алфавит, который содержит 33 буквы и знак «пробел» для разделения слов.

По формуле Хартли

Но в словах русского языка различные буквы встречаются неодинаково часто. Ниже приведем таблицу 2 вероятностей частоты употребления различных знаков русского алфавита, полученную на основе анализа больших объемов текстов.

Таблица 2 – частотность букв русского алфавита

i	символ			символ		i	символ
	_	0,175		Л	0,035		Б	0,014
	О	0,090		К	0,028		Г	0,012
	Е	0,072		М	0,026		Ч	0,012
	Е	0,072		Д	0,025		Й	0,010
	А	0,062		П	0,023		Х	0,009
	И	0,062		У	0,021		Ж	0,007
	Т	0,053		Я	0,018		Ю	0,006
	Н	0,053		Ы	0,016		Ш	0,006
	С	0,045		З	0,016		Ц	0,004
	Р	0,040		Ь	0,014		Щ	0,003
	В	0,038		Ъ	0,014		Э	0,003
							Ф	0,002

В случае, когда вероятности результатов опыта неодинаковы, применим формулу Шеннона:

В случае равновероятности событий: и формула Шеннона переходит в формулу Хартли.

Возьмем формулу Шеннона для подсчета: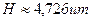

Ответ: 4,72 бита

Пример 2. В коробке 3 синих и 21 красных кубиков. Какое количество информации несет сообщение, что из коробки достали синий кубик?

Для решения этой задачи можно использовать следующие формулы:

Вероятность события: p=K/N,

где N - общее число возможных исходов

K - число возможных исходов интересующего нас события

Количество информации: i=log₂(1/p)

N/K= 2ⁱ

Решение:

N=3+21=24 всего кубиков

K=3 – синих (его достали)

N/K=24/3=8

2ⁱ=8

i=3 бита

Ответ: 3 бита.

Пример 3. В колоде содержится 32 карты. Из колоды случайным образом вытянули туза, потом его положили обратно и перетасовали колоду. После этого из колоды опять вытянули этого же туза. Какое количество бит информации в сумме содержат эти два сообщения?

Решение:

N=32

K₁=4 (4 туза в колоде)

K₂=1(в колоде один туз определенной масти, который был вытянут в первый раз)

N/ K₁=32/4=8

2ⁱ¹=8

i₁=3 бита

N/ K₂=32/1=32

2ⁱ²=32

i₂=5 бита

i₁₊ i₂=3+5=8 бит

Ответ: 8 бит

Дата добавления: 2015-08-27