Матрицы, определители, с-мы лин. ур-ний.

1.Матрица —прямоугольная табл. вида: (mxn).

---нижняя треугольная М.

Св-ва:

(А+В)+С=A+(В+C)---ассоциативность. А+В=В+А

А+0=А А-А=А+(-А)=0

А=(а_ij) -число •А=( • а_ij) 1*А=А

(А+В)= А+ В---дистрибутивность

2. А=А_MxN согласованные

В=В_NxR

С=АВ С=С_MxR

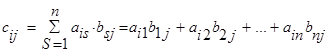
Св-ва:

2.1. А•0=0•А=0 2.3. (АВ)С=А(ВС) 2.5. А(В+С)=АВ+АС

2.2. A•I=I•A=A 2.4. (А+В)С=АС+ВС 2.6. (АВ)=( А)В=А( В)

А•В ≠ В•А --- в общих случаях

Док-во к 2.3.: А_mxn B_nxk C_kxl

D=AB ------ mxk; DC=mxl; E=BC -------nxl; AE=mxl

3. Если А^т=А, то А---симметричная. (а_ij=a_ji)

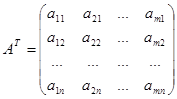Св-ва:3.1. (А^Т)^Т=А 3.2.( А)^Т= А^Т 3.4. (АВ)^Т=В^ТА^Т 3.3. (А+В)^Т=А^Т+В^Т

4. Перестановкой из n эл-тов наз всякое положение эл-тов мн-ва М в определённом порядке (или упорядоченный набор этих эл-тов).

Теорема1: Число всех перестановок из n эл-тов P_n=n!

Док-во: n способов для заполнения 1-го места

(n-1) для --//-- 2-го места

Для двух мест n(n-1) --- способов. И т. д.

5. Перестановка наз чётной, если её число инверсий чётное (и наоборот).

(инверсия – если , при i>j, то пара АЛи и АЛж образует ИНВЕРСИЮ)

Теорема2: Транспозиция меняет чётность перестановки.

Док-во: Транспозиция соседних эл-тов меняет чётность перестановки

Была (…,АЛ_и,АЛ_и+1,…)---чётная. Стала (…,АЛ_и+1,АЛ_и,…)---нечётная

Число инверсий при транспозиции соседних эл-тов меняется на 1, тем самым меняется чётность.

6. Определителем n-го порядка матрицы А называется число detА или |А| и равно алгебраической сумме всяких эл-тов, взятых ровно по одному из каждой строчки и каждого столбца, снабжённых знаком (-1)^s+t, где s-число инверсий перестановки первых индексов данного произведения, а t- --//-- вторых индексов --//--, т. е. ,

,

Св-во1: Определитель не меняется при транспонировании.

Док-во: |А^т|=|А|

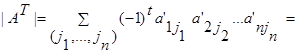
a’ --- транспонированное a

7. Св-во2: Если матрица А имеет нулевую строку, то её определитель равен 0.

Док-во: Согласно общему определению определителя в каждом произведении будет множитель нуль, зн. и сумма равна 0.

Св-во3: Общий множитель какой-либо строки можно выносить за знак определителя, а зн. и столбца. Док-во:

8. Св-во4: Если в опр-ле поменять местами две строчки, то изменится знак опр-ля.

Док-во:

; ; S-нечётное.

Св-во5: Если в опр-ле есть две равные строки, то он равен 0.

Док-во: Пусть в опр-ле m- тая и k -тая строчки равны. Поменяем их местами и получим: |А|=-|А| |А|=0

Св-во6: Если в опр-ле есть две пропорциональные строки, то опр-ль равен 0.

Док-во: Если вынести коэффициент пропорциональности , то получим две равные строки, при этом опр-ль станет равным 0.

9. Св-во7: Если в опр-ле строка представлена в виде суммы вида , то опр-ль равен сумме двух опр-лей, у которых в m -той строке первые слагаемые у первого опр-ля и вторые слагаемые у второго опр-ля. Все остальные эл-ты остаются неизменными.

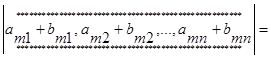
Док-во:

Св-во8: u₁, u₂,…, u_k---некоторые строки матрицы

₁, ₂,…, _k R---числа

₁u₁+ ₁u₁+…+ ₁u₁---линейная комбинация строк u₁, u₂,…, u_k

Если в опр-ле явл. линейной комбинацией др. строк, то опр-ль=0

Док-во: (из св-ва 7)

Св-во9: Если к какой-либо строке матрицы добавить другую строку этой матрицы, умноженную на число, то опр-ль не изменится.

Док-во: (из св-тв 7-8).

10. Св-во10: Опр-ль ∆-ной матрицы равен произведению диагональных эл-тов.

Св-во11: Опр-ль матрицы след. вида:

, где А₁,А₂,…,А_К---квадратные матрицы, А_i---блочные матрицы.

11. Теорема (о разложении опр-ля по эл-там строки)

Сумма произведений эл-тов строки матрицы А на их алгебраические дополнения равна опр-лю данной матрицы.

Док-во: В опр-ле матрицы А представим в виде суммы n слагаемых:

a_k1+0+0+…+0, 0+a_k2+0+…+0, …, 0+0+…+a_kn

Тогда:

Загоняем переставлением 1 на место [] и получим:

---

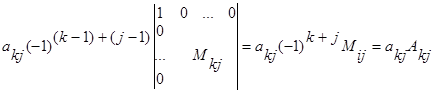
Дата добавления: 2015-08-27