Квадратичные формы

11. Квадратичные формы. Квадратичной формой от нескольких переменных называется однородный многочлен второй степени от этих переменных. Например, квадратичная форма от трех переменных

x_lt х₂, x_s в общем случае имеет вид

/=•= а_их\ + a_zzx\ + а_зах! + 2а₁₂*₁х_! + 2а₁₃л;₁лг₃ + 2а_м*,*₈, (39)

где а_ц, я_2а,..., а₂₃— некоторые числовые коэффициенты (а двойки поставлены для упрощения получающихся формул). Матрицей такой формы называется симметрическая матрица

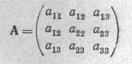
С помощью этой матрицы форму (39) можно переписать в виде F = (вц*! + а_пх₂ + а₁₃х_&) x_t + (a_nXi + а₂₂лг_а + а.,₃х₃) x_z +

v

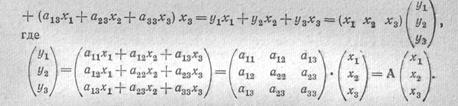
Значит, если ввести числовой вектор

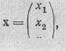
то получим

W F = x*Ax. (40)

Обратно, если форма представлена в виде (40), причем матрица А симметрическая, то А является матрицей этой формы.

Проведем теперь какую угодно линейную замену переменных вида (30) или, коротко,

х = Нх'. (41)

Тогда в силу формулы (4) х*=х'*Н*, откуда

F = х'*Н*АНх' = х'* (Н*АН) х',

т. е.

/^г=х'*А'х', где А' = Н*АН. (42)

Однако матрица А' симметрическая, так как в силу формулы (4) А'* = (Н*АН)* = Н*А*Н** = Н* АН = А'.

Значит, А' и служит матрицей квадратичной формы после замены переменных.

Итак, при подстановке (41) матрица квадратичной формы пре­образуется по формуле (42). Если, в частности, считать матрицу Н ортогональной, то в силу формулы (34) получаем, что А' = Н~^ТАН. Как было показано в п. 10, всегда можно подобрать матрицу Н

так, чтобы A'=dlag (А^Дз, ^sK где на диагонали стоят собственные-значения матрицы А. Но тогда квадратичная форма F в новых пе­ременных приобретает диагональный вид

F = K₁x'₁* + b_tx'S + b_tx'_t*. (43)

Итак, квадратичную форму (39) можно с помощью преобразования (30) с ортогональной матрицей привести к диагональному виду (43), где K_t, K%, A,₈ — собственные значения матрицы А.

Указанное формальное преобразование имеет следующий геомет­рический смысл. Рассмотрим матрицу А как матрицу некоторого линейного преобразования А в декартовом базисе с координатами ^xi> ^Х2> ^хз- Тогда переход (41), приводящий квадратичную форму F к виду (43), отвечает переходу к новому базису, составленному из собственных векторов преобразования А.

В п. 8 (формула (33)) мы показали, что при любой замене вида (31) оп­ределитель det(A— Kl) не меняется. Значит, если разложить этот определитель по степеням X, то коэффициенты при этих степенях также не будут меняться; эти коэффициенты будут инвариантными относительно замены декартовых координат. Например, квадратичная форма от двух переменных при обоз­начениях, принятых в аналитической геометрии, имеет вид

Ах² + 2Вху + Су*, т. е. ее матрица такова:

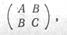
а характеристическое уравнение

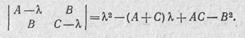
Значит, выражения А-\-С и АС — В^а инвариантны относительно замены де­картовых координат (см. п. 11.13).

12. Упрощение уравнений линий и поверхностей второго по­рядка. Преобразование квадратичной формы, описанное в п. 11, применяется, в частности, к упрощению уравнений линий и поверх­ностей второго порядка. Остановимся на уравнении поверхностей, так как упрощение уравнений линий второго порядка описано в п. 11.13.

Пусть поверхность второго порядка задана в обычном для ана­литической геометрии виде (Х.13). Переход к новой декартовой системе координат с тем же началом, как было показано в п. 9, сводится к замене переменных

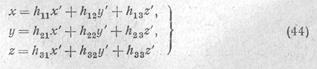
с ортогональной матрицей перехода Н. (Ясно, что если начало ко­ординат не заменяется, то координаты точек преобразуются по тем же формулам, что координаты векторов.) При подстановке этих выражений в уравнение (Х.13) группа членов второй степени и группа членов первой степени преобразуются независимо друг от друга. Если следить сначала только за группой членов второй сте­пени (квадратичной формой), то на основании п. 9, мы получаем, что всегда можно выбрать систему координат х', у', z' так, что эта группа членов приобретет диагональный вид. Поэтому все уравнение после преобразования будет иметь вид

V<r'² + b_zy'* + V» + G'x' + H'y'+ I'z' + J =* 0; (45)

здесь K_lt К_г, К₃ — корни уравнения

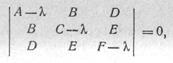
а О', Н', /'—некоторые новые коэффициенты при членах первой степени, которые сами получатся после подстановки (44). Уравне­ние (45) — это уравнение (Х.14) в других обозначениях; его иссле­дование описано в п. Х.11.

§ 4. Нелинейные отображения

13. Общие понятия. Начнем с отображения плоскости в плоскость. Для этого предположим, что имеются две плоскости (Р) и (Р), которые, впрочем, могут быть совмещенными. Пусть каждой точке М из плоскости (Р) (или из некоторой ее области) но опреде-

ленному закону соответствует оп­ределенная точка М плоскости (Р). Тогда говорят, что задано отоб­ражение плоскости (Р)_(или ее области) в плоскость (Р), Как было отмечено в конце п. VIП. 11 при рассмотрении отображений специального _вида, при отобра­жении (Р) в (Р) линии переходят в линии; фигуры в плоскости (Р) переходят в фигуры в плоско­сти (Р), хотя при этом переходе форма фигуры может так изме­ниться (рис. 224), что по прооб-

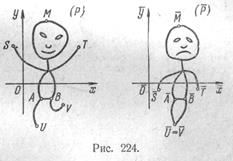
ра-jy в плоскости (Р) будет трудно узнать образ в плоскости (Р) и наобо­рот. Возможны также случаи вырождения, когда, например, отдельные фигуры при отображении «сплющиваются» в линии или даже в точки.

Иногда приходится рассматривать обратное отображение, которое по­лучится, если задавать образ в (Р) и искать прообраз в (Р). При этом, подобно обратной функции (п. 1.21), может получиться осложнение: обратное

отображение может оказаться многозначным. Так будет, если какие-либо две точки плоскости (Я), как U и V на рис. 224, переходят в одну и ту же точку плоскости (Р), так как такая точка будет иметь по меньшей мере два прообраза.

Если не только само отображение, но и обратное отображение являются однозначными, то рассматриваемое отображение называется взаимно однознач­ным. Если же отображение не взаимно однозначное, но не вырождается, то плоскость (Р) можно разбить на части, на каждой из которых отображение будет взаимно однозначным.

Отображения описываются аналитически с помощью систем координат. Для этого предположим, что в плоскости (Р) введена система декартовых координат х, у, а в плоскости (Р) — система координат х, у; эти системы также могут быть совмещенными. Тогда если задать координаты х, у точки М, то координаты х, у точки М однозначно определяются. Другими слова­ми, отображение определяется зависимостями

х = х(х, у); у = у (х, у). (46)

При обратном отображении мы задаем в этих формулах х и у и находим х и у; для взаимной однозначности отображения нужно, чтобы при этом получалось не более одного решения.

Аналогично определяется отображение трехмерного пространства в трех­мерное; такое отображение определяется, взамен (46), формулами

~х=1с(х, у, г), ~у=~у(х, у, г), ~г — 7(х, у, г). (47)

Можно рассматривать и отображения друг в друга пространств различ­ных размерностей. Например, формулы

х = х(х, у), у = у(х, у) ~z = z(x, у)

определяют отображение плоскости в трехмерное пространство.

Формулы (Х,5) можно рассматривать как формулы, определяющие отображение от-мерного пространства с координатами t_lt t₂,.., t_m в n-мер­ное пространство с координатами x_lt x₂..... х_п. При этом система координат

не обязана быть декартовой.

14. Нелинейное отображение в малом. Рассмотрим отображение, опреде­ленное формулами^б), вблизи некоторой точки УИ₀ (х„; у„), которая отобра­жается в точку М₀ (х₀; //„). Поскольку с точностью до малых высшего порядка приращение любой функции можно ааменпть ее дифференциалом (п. IX.11), то, пренебрегая этими малыми, получим

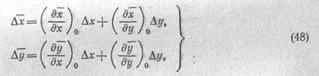
где Ьх = х — х₀, &х=х —л'₀ и т. д. (можно сказать, что это—декартовы координаты, отсчитываемые соответственно от М_а и М_й), а индекс «нуль» указывает на то, что производные берутся в точке М₀. Сравнивая формулы.. (48) с формулами (27), мы заключаем, что нелинейное отображение в беско­нечно малой окрестности любой точки является с точностью до малых высшего порядка линейным.

На основании п. 6 мы заключаем, что если определитель

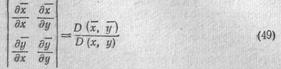
(обозначение см. в п. IX.13) в какой-либо точке М₀ не равен нулю, то рассматриваемое отображение в малой окрестности этой точки является взаимно однозначным и даже с точностью до малых высшего порядка аффинным. При этом абсолютное значение определителя (49) равно коэффи­циенту изменения площадей бесконечно малых фигур при рассматриваемом отображении; этот коэффициент

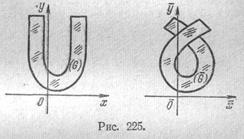
уже не постоянен во всей плоскости, как для линейного отображения, а принимает, во­обще говоря, в различных точках разные значения. Это, в частности, дает возможность приписать самостоятельный смысл знаменателю и числителю в правой части (49): они равны площади бесконечно малой фи­гуры до и после отображения. Если в какой-либо точке якобиан (49) равен нулю, то

в этой точке рассматриваемое отображение вырождается, а именно, пло­щадь бесконечно малой фигуры после отображения становится малой выс­шего порядка. Если же якобиан (49) тождественно равен нулю, то отобра­жение вырождается во всей плоскости, так что при отображении размерность понижается: плоскость отображается на некоторую линию, не обязательно прямую, или даже в точку.

Не следует думать, что ос л и якобиан (49) не равен нулю ни в какой точке некоторой конечной области, то отображение будет в этой области взаимно однозначным. Отображение может быть не нырожденным ни в какой точке, но тем не менее не быть взаимно однозначным (см., например, рис. 225).

Аналогичными свойствами обладает отображение трехмерного простран­ства в трехмерное; это отображение может задаваться ^формулами (47).

Здесь также существенное значение имеет якобиан ' •', абсолютной

значение которого равно коэффициенту изменения объемов бесконечно малых тел. (Каков геометрический смысл знака якобиана?)

В случае, если этот якобиан тождественно равен нулю, может возник­нуть вопрос о «степени» вырождения, т. е. о том, отобразится ли простран­ство х, у, z на поверхность или на линию (или даже на точку) пространства х, у, г. Ответ на этот вопрос вытекает из рассмотрений п. 6 и того, что каждое отображение в бесконечно малом является линейным. Надо раст смотреть матрицу

Ее ранг в любой точке меньше трех (почему?). Если он равен двум (в некоторых точках допускается понижение ранга), то пространство х, у, г отображается на двумерную поверхность. Если он нигде не превышает единицы, но не равен нулю тождественно, то отображение происходит на одномерную линию. Наконец, если он тождественно равен нулю (это значит, что все элементы матрицы (50)_тождеетвенно равны нулю, что будет только для тождественно постоянных х, у, I), то все пространство отображается на точку.

Аналогичная картина получается при отображении пространств любых, не обязательно одинаковых размерностей друг в друга. Мы уже говорили, что формулы (Х.5) можно рассматривать как формулы, определяющие ото­бражение m-мерного пространства с координатами t_lt t_z,..., t_m в n-мерное пространство с координатами %, x_z,..., х_п. Чтобы выяснить, какой размер­ности многообразие получится в результате этого отображения, нужно соста­вить матрицу размера пхт

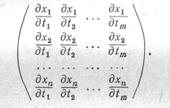
Если ранг этой матрицы равен k (причем в некоторых точках допускается понижение ранга), то и указанная размерность равна k.

15. Функциональная зависимость функций. Результаты п. 14 можно применить к понятию «функциональной зависимости» системы функций. Допустим сначала, что заданы три функции от трех независимых переменных

fj (х, у, г), F₂ (х, у, г), F₃ (х, у, г). (51)

Эти функции называются функционально зависимыми друг с другом, если между ними имеет место соотношение вида

Ф(Р₁(х,у,г), F_t(x, у, г), F₉(x, у, г))**0, (52)

где Ф—некоторая функция трех переменных, Ф = ф(Х, ^, v), сама по себе не тождественно равная нулю. В противном случаи функции (51) называются функционально независимыми. Разрешая соотношение (52) относительно одной из переменных Fj, F₂, F₃, можно сказать также, что функции (51) называ­ются функционал!,но м.-шисимымн, если одна из них является функцией остальных.

Например, функции

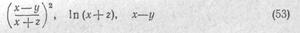
функционально зависимы, так как если их обозначить через F_it F₂ и F_s, то

F^'-fi-a

Чтобы установить признак функциональной зависимости в общем случае, рассмотрим вспомогательное отображение

K = F₁(x, у, г), |

р = Р₂(х, у, г), 1 (54)

v=F_a(x, у, г), j

Для функциональной зависимости системы (51) нужно, чтобы существовало соотношение (52), т.е. соотношение Ф (Я,, ^, v)=0, справедливое для всех х, у, г. Оно определяет в пространстве К, [г, v некоторую поверхность, и мы получаем, что для функциональной зависимости функций (51) нужно, чтобы при отображении (54) пространство х, у, г переходило в поверхность в пространстве К, Ц, v, т. е. чтобы это отображение было вырожденным. Применяя результат п. 14, приходим к условию

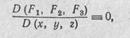
необходимому и достаточному для функциональной зависимости функций (51). (Проверьте выполнение условия (55) для функций (53).) Если же ранг матрицы

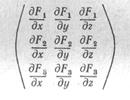
равен единице, то, как мы видели в п. 14, пространство к, у, г при отобра­жении переходит в линию в пространстве К, ц, v. Пользуясь уравнениями линии (Х.2), заключаем, что в данном случае функции F_L, F₂, F₃ связаны друг с другом двумя независимыми соотношениями вида (52).

Аналогичный результат получается и в том случае, когда число незави­симых переменных и рассматриваемых функций от них различно. Например, две функции от трех переменных F_t (х, у, г), F₂ (х, у, г) будут функционально зависимыми, если при отображении

X — F,(x, у, г), n="F,U, у, г)

пространство х, у, г переходит и линию па плоскости К, ц (с некоторым уравнением Ф (К, (i) = 0). Согласно п. 14 условие для этого состоит и том, чтобы ранг матрицы

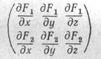
был меныье двух, т. е. чтобы

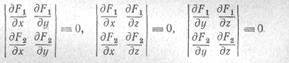
Условия функциональной зависимости системы из любого числа функций от любого числа аргументов выглядят аналогично Отметим, что если функ­ций больше, чем аргументов, то такая система функций всегда функционально зависима.

Полученный физический смысл градиента показывает также, что градиент инвариантно связан с рассматриваемым полем, т. е. остается неизменным (инвариантным) при замене декартовых осей. (Этого не было видно из определения градиента (2), данного в «неинвариант­ной» форме, «привязанной» к какой-то одной системе координат.) Более того, если задано поле и, то' в каждой точке пространства можно найти направление и скорость наибыстрейшего возрастания поля и; так можно найти вектор grad ц, не прибегая к координатам и к заданию и (х, у, z). Итак, градиент скалярного поля образует вполне определенное векторное поле.

Аналогичное требование инвариантности ставится для всех основных поня­тий теории векторного поля, которая в этой главе не будет изучаться. Дело в том, что при замене осей декартовой системы координат, хотя векторы ос­таются неизменными, инвариантными, но их проекции меняются. Таким образом, если какое-либо понятие теории векторного поля сформулировано с помощью координат или проекций этого поля, то надо проверить, что это понятие удовлетворяет требованию инвариантности относительно изменения этих координат и проекций при повороте осей координат.

Покажем применение понятия градиента к вычислению скорости измене­ния поля вдоль траектории. Пусть задано поле ir. вообще говоря, нестацио­нарное, т. е. и — и(х, у, z, t). Пусть, далее, задан закон движения r = r(t) некоторой частицы М. Если рассматривать значение и в ' М по мере движе­ния, то это значение будет представлять собой сложную функцию времени: u = u(x(t), у (t), г (t), t). Для вычисления искомой скорости изменения этого значения можно применить преобразования, аналогичные приведенным выше, что даст значение полной производной

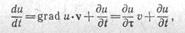
dr ди

где v = -tt—вектор скорости движения частицы, а ^- — производная по направ­лению касательной к траектории.

Если поле стационарное (•?:=0), то справа остается только первое

слагаемое. Таким образом, оно дает скорость изменения поля, полученную только за счет перехода точки М вдоль траектории от одних значений и к дру­гим; например, если и —температура, то за счет перехода из менее нагретой части пространства в более нагретую и т. и. Эта скорость называется переносной (конвективной). Второе слагаемое дает скорость изменения поля в неподвиж­ной точке, полученную из-за нестационарности поля; эта скорость называется местной (локальной). В общем случае действуют оба указанных фактора и скорость изменения поля вдоль траектории складывается из переносной и местной скоростей изменения поля.

2. Поверхности уровня. Поверхности уровня для поля и(х, у, z) (см. п. IX.7) — это поверхности, на которых поле имеет постоянное значение, и (х, у, z) = const; в зависимости от физического смысла поля они могут называться изотермическими, изобарическими и т. п. поверхностями. Между этими поверхностями и градиентом поля имеется простая связь: в каждой точке М градиент поля нормален (т. е. перпендикулярен касательной плоскости) к поверхности уровня, проходящей через М.

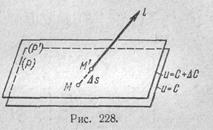
Действительно (рис. 228), если АС малб, то вблизи М поверх­ности и—С и u = C+AC можно считать почти плоскими и

ди Аи ДС и а,

^-«-г-=д-. по ясно, что As будет самым малым, а потому про­изводная -^ — самой большой, если / направлено по нормали к поверх-

ности. Отсюда и следует наше утверждение.

Из него, в частности, полу­чаем решение следующей задачи: найти уравнение касательной плоскости,, проведенной в точке М₀(х_й; у₀; г₀) к поверхности. (L), имеющей уравнение F(x,y,z) = 0. Для решения этой задачи рас­смотрим на минуту поле в про-

странстве, определенное по формуле u = F(x, у, z). Тогда (L) будет одной из поверхностей уровня этого поля, так как на ней и — 0. Но тогда вектор

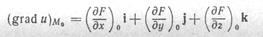
(индекс «нуль» указывает, что рассматриваемые производные берутся в точке Ж₀) перпендикулярен к искомой касательной плоскости. Согласно п. Х.7 (задача 2) получаем уравнение этой плоскости:

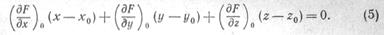
Последнее уравнение можно записать в форме dF — Q; подумайте, как его можно было бы вывести непосредственно.

Уравнение поверхности, к которой надо провести касательную плоскость, может быть задано в форме z=f(x, у). Тогда достаточно это уравнение переписать в виде z — f(x, </) = 0, обозначить левую

часть через F(x, у, z) и применить результат (5): —(д-) (х — х₀) —

Дата добавления: 2015-08-27