Постановка задачи целочисленного линейного программирования

Глава 3. Метод ветвей и границ решения задач целочисленного линейного программирования

Постановка задачи целочисленного линейного программирования

Задача линейного программирования, переменные которой могут принимать только целые значения, является задачей целочисленного линейного программирования:

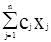
где 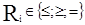; x_j - переменные, a_ij, b_i, c_j - константы.

Записанная в таком виде задача представляет собой полностью целочисленную задачу. Существуют, кроме того, частично целочисленные задачи, в которых ограничения целочисленности наложены только на часть переменных, а остальные переменные могут быть как целыми, так и дробными.

Примером целочисленной задачи в экономике может служить задача производственного планирования, в которой в качестве продукции выступают корабли, дома, вагоны и т.п. предметы, выпуск которых нельзя измерить в непрерывной шкале. Часто переменные в экономико-математических моделях измеряются в количестве человек, которое также не может быть дробным.

На первый взгляд, тривиальным подходом к решению такой задачи является решение задачи линейного программирования без ограничений целочисленности и последующее округление полученного решения до целых. Однако в общем случае такой подход неверен, так как он может привести к одной из двух ошибок. Во-первых, при округлении возможен выход за пределы ОДП, т.е. полученное решение не будет удовлетворять ограничениям. Во-вторых, даже оставшись в пределах ОДП, можно в результате получить неоптимальное решение.

Поэтому округление допустимо использовать лишь в тех случаях, когда по своему экономическому смыслу целочисленные переменные не представляют особо ценные объекты, либо в модели рассматривается очень большое количество таких объектов; т.е. нет необходимости получить точное решение. В противном случае задача должна ставиться, как целочисленная, и к ее решению необходимо применить специфические методы, которые обычно относятся к одной из трех групп:

1. Метод ветвей и границ.

2. Методы отсечения.

3. Методы динамического программирования.

Здесь будет рассмотрен метод из первой группы. Однако, предварительно сформулируем ряд определений.

Дата добавления: 2015-08-27