
Читайте также:
|
Транспонированием называется такое преобразование матрицы, при котором строки и столбцы меняются местами с сохранением их номеров. Обозначается транспонирование значком «Т» наверху – АТ.
Пусть дана матрица (1). Переставим строки со столбцами. Получим матрицу
 ,
,
которая будет транспонированной по отношению к матрице А. В частности, при транспонировании вектора-столбца получается вектор-строка и наоборот.
Произведением матрицы А на число l называется матрица, элементы которой получаются из соответствующих элементов матрицы А умножением на число l:
l A = (l ai j).
Суммой двух матриц А = (ai j) и B = (bi j) одного размера называется матрица C = (cij) того же размера, элементы которой определяются по формуле ci j = ai j + bi j.
Произведение АВ матрицы А на матрицу В определяется в предположении, что число столбцов матрицы А равно числу строк матрицы В.
Произведением двух матриц А = (ai j) и B = (bj k), где i =  , j=
, j= 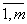 , k=
, k=  , заданных в определенном порядке АВ, называется матрица С = (c i k), элементы которой определяются по следующему правилу:
, заданных в определенном порядке АВ, называется матрица С = (c i k), элементы которой определяются по следующему правилу:
c i k = ai 1 b1 k + ai 2 b2 k +... + ai m bm k = 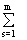 ai s bs k. (2)
ai s bs k. (2)
Иначе говоря, элементы матрицы-произведения определяются следующим образом: элемент i-й строки и k-го столбца матрицы С равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы k-го столбца матрицы В.
Пример 1. Найти произведение матриц 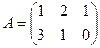 и
и  .
.
Решение. Имеем: матрица А размера 2х3, матрица В размера 3х3, тогда произведение АВ = С существует (матрица С размера 2х3) и элементы матрицы С равны
с11 = 1×1 +2×2 + 1×3 = 8, с21 = 3×1 + 1×2 + 0×3 = 5, с12 = 1×2 + 2×0 + 1×5 = 7,
с22 =3×2 + 1×0 + 0×5 = 6, с13 = 1×3 + 2×1 + 1×4 = 9, с23 = 3×3 + 1×1 + 0×4 = 10.
 , а произведение BA не существует.
, а произведение BA не существует.
Пример 2. В таблице указано количество единиц продукции, отгружаемой ежедневно на молокозаводах 1 и 2 в магазины М1, М2 и М3, причем доставка единицы продукции с каждого молокозавода в магазин М1 стоит 50 руб., в магазин М2 - 70, а в М3 - 130 руб. Подсчитать ежедневные транспортные расходы каждого завода.
| Молокозавод | Магазин | ||
| М1 | М2 | М3 | |
Решение. Обозначим через А матрицу, данную нам в условии, а через В - матрицу, характеризующую стоимость доставки единицы продукции в магазины, т.е.
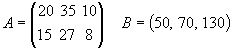 ,
,
Тогда матрица затрат на перевозки будет иметь вид:
 .
.
Итак, первый завод ежедневно тратит на перевозки 4750 руб., второй - 3680 руб.
Дата добавления: 2015-08-27; просмотров: 40 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Матрицы. Операции над матрицами | | | Джоконда. |