Принципы статистического анализа. Погрешности измерений.

Имеется определенная степень ненадежности в каждом лабораторном исследовании. Повторное исследование образца в идентичных условиях дает не идентичные результаты вследствие влияния случайных погрешностей. Результаты лабораторных исследований образуют вариационный ряд с характерным для него распределением большинства величин вблизи его центральной части и рассеиванием к краям ряда, создавая определенное распределение. Подобное распределение называется нормальным распределением. Закон распределений называется нормальным законом распределения случайных величин Гаусса. Случайные погрешности, как правило распределены по нормальному закону. Кривая нормального распределения имеет колоколообразную форму и характеризуется двумя параметрами: средняя арифметическая величина (x среднее) и среднее квадратичное отклонение (S). Характер распределения полученных величин можно ориентировочно определить путем представления этих величин графически на гистограмме.

Средняя арифметическая величина:

Альтернативной величиной средней арифметической, является медиана, которая используется в случае, когда имеются экстремальные величины и средняя может не давать истинной картины.

Разброс результатов около средней величины можно выразить средним квадратичным отклонением, которое рассчитывается с помощью уравнения:

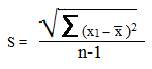
Среднее квадратичное отклонение отражают в виде процента относительной средней и коэффициента вариации (V).

Будучи числом без единиц измерения оно очень упрощает сравнение средне квадратичных отклонений результатов исследований, выраженных в разных единицах.

Индекс средне квадратичного отклонения выражает положение результата в распределении независимо от концентрации (JS).

Средне квадратичное отклонение средней или стандартную ошибку средней рассчитывают по формуле:

Таким образом с хорошо налаженным контролем качества ненадежность результата можно снизить, значительно уменьшив ошибки.

Дата добавления: 2015-08-27