Системы счисления. Система счисления — это совокупность цифровых знаков и правил их записи

Система счисления — это совокупность цифровых знаков и правил их записи, применяемая для однозначной записи чисел. Все системы счисления подразделяются на позиционные и непозиционные.

Непозиционной называется такая система счисления, в которой значение цифры не зависит от ее положения в ряду цифр, изображающих число. Древние египтяне применяли систему счисления, состоящую из набора символов, изображавших распространенные предметы быта. Совокупность этих символов представляла число. Расположение символов в числе не имело значения, отсюда и появилось название – непозиционная система счисления. Примером является римская система счисления, в которой для обозначения отдельных чисел используются буквы римского алфавита. Цифры в римской системе обозначаются различными знаками:

1 — I; 3 — III; 5 — V; 10 — X; 50 — L; 100 — С; 500 — D; 1000 — М. Запись числа осуществляется по каждый меньший знак, поставленный справа, он прибавляется к его значению, а слева — вычитается из него: так, ХС — 90; СХ — 110; MCMLXXXVIII — 1988. Выполнять арифметические действия в непозиционных системах неудобно. Поэтому в настоящее время эти системы не используются для расчетов.

Позиционной называется такая система счисления, в которой значение цифры зависит от ее положения в ряду цифр (позиции), изображающих число.

Первая известная нам позиционная система счисления – шестидесятеричная вавилонская система счисления. Следы этой системы счисления сохранились и сегодня в способах измерения и записи величин углов и времени.

Сегодня мы пользуемся индо-арабской системой счисления, где имеется десять цифр: от 0 до 9. Эта система счисления получила название десятичной.

Позиционная система счисления (ПСС) характеризуется количеством различных цифр, используемых для записи чисел. Максимальное количество различных цифр, используемых для записи чисел в данной системе счисления, называется основанием системы счисления. Основание системы счисления определяет ее название.

В позиционной системе счисления каждый разряд имеет вес. Весом разряда называется число bⁿ, где b – основание системы счисления, а n – номер разряда. Например, в десятичном числе 1276 цифра 2 имеет значение 200, т.к. вес разряда, в котором записана эта цифра, равен 100, т.е. 10² = 100.

Любое число, записанное в ПСС с основанием p, может быть представлено в следующем виде:

(2.1)

где 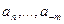— любая цифра (символ), используемая в данной ПСС из множества {0,1,..., р — 1}; n, …, m — номера разрядов числа; р — основание ПСС, которым может быть любое целое число, кроме и ; 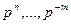— веса разрядов. Например, число = 1235,87 по (2.1) имеет вид:

В ЭВМ применяют ПСС с основанием 2 - двоичную. Поскольку число, записанное в двоичной системе счисления очень громоздкое, то для удобства работы применяют восьмеричную и шестнадцатеричную системы счисления. В таблице 2.1 показано соответствие записи чисел в десятичной, восьмеричной и шестнадцатеричной системах счисления.

Таблица 2.1

Соответствие записи чисел в десятичной, восьмеричной и шестнадцатеричной системах счисления

			A
			B
			C
			D
			E
			F

Двоичная ПСС получила самое широкое применение в ЭВМ благодаря следующим достоинствам. Удобства кодирования информации и простота выполнения арифметических операций.

Т.к. одно из необходимых условий работы компьютера – наличие напряжения, вся информация в компьютере представлена с помощью напряжений, т.е. закодирована какими то напряжениями. Для удобства кодировки полагают, что если напряжение есть, то это состояние обозначают 1, если нет, то 0. Эти цифры называются двоичными (от английского binary digit). Сокращение этого выражения привело к появлению термина bit, ставшего названием разряда двоичного числа. Итак, две цифры 0 и 1 есть, а как записать другие цифры в компьютере. Для этого используется код числа – т.е. комбинация 0 и 1. Как оказалось, реализация элементов, которые должны различать одно из двух состояний (0 или 1) и их комбинаций, оказывается проще и надежнее, чем реализация элементов, которые должны различать одно из 10 состояний.

Для кодирования символьной информации используются кодовые таблицы. Сегодня самая распространенная кодовая таблица – это ASCII – (American Standard Cord for Information Interchange) американский стандарт. В системе ASCII закреплены две таблицы кодирования – базовая и расширенная. Базовая таблица закрепляет значение кодов от 0 до 127, а расширенная относится к символам с номерами от 128 до 255.

Первые 32 кода базовой таблицы отданы производителям аппаратных средств (в первую очередь производителям компьютеров и печатающих устройств). В этой области размещаются так называемые управляющие коды, которым не соответствуют никакие символы языков, и эти коды не выводятся ни на экран, ни на устройства печати, но ими можно управлять тем, как производится вывод прочих данных.

Начиная с кода 32 по код 127 размещены коды символов английского алфавита, знаков препинания, цифр, арифметических действий и некоторых вспомогательных символов. Принцип построения кодовых таблиц следующий. Количество всех символов (английские и русские большие и малые буквы, цифры, знаки препинания и т.п.) менее 255. Максимальное число, которое можно записать в 1 байт – это 8 единичек = 255. Поэтому используя 1 байт можно закодировать все символы. Таблицу строят следующим образом: по горизонтали и по вертикали записывают числа от 0 до 15. Получим таблицу 16 строк на 16 столбцов, т.е. 256 клеточек. В каждую клетку записывают какой-то символ. Код символа получают записав в шестнадцатеричной системе счисления число, которое состоит из номера столбца и номера строки. Например,

			…			…	F
					P
				A	Q
				B	R
				C	S
				D	T
				E
…
F				O

Код латинской буквы А – 41₁₆. Вначале указываем № столбца, затем № строки. В десятичной системе это 65. Пользоваться 16-ой системой счисления удобней, код получается проще.

Процесс синтеза схем ЭВМ упрощен, так как обозначение переменных и функций в используемом математическом аппарате алгебры логики, принимающих два значения 0 или 1, совпадает с двоичными цифрами.

В то же время громоздкость записи чисел в двоичной ПСС и трудность их восприятия человеком (см. табл. 2.1) приводит к необходимости перевода исходных данных (чисел) из десятичной системы счисления в двоичную, а результатов — из двоичной в десятичную. Эти переводы осуществляются в ЭВМ автоматически по определенным программам.

В соответствии с формулой (2.1) числа в разных ПСС можно представить следующим образом:

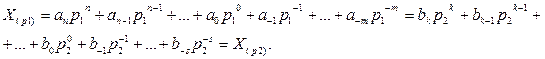(2.2)

Следовательно, в общем виде задачу перевода числа из ПСС с основанием в ПСС с основанием , формулируемую в виде:

(2.3)

можно представить как задачу определения коэффициентов нового ряда, изображающего число в ПСС с основанием .

Решение (2.3) непосредственно в виде (2.2) осуществляют при "ручном" способе перевода чисел из одной ПСС в другую. Для "машинной" реализации перевода и выполнения арифметических операций применяют методы, которые мы рассмотрим параллельно с ручными операциями.

Дата добавления: 2015-08-27