
Читайте также:
|
Рассмотрим графы  и
и 
а) Дополнением графа  называется граф
называется граф  множеством вершин которого является множество
множеством вершин которого является множество  а множеством его рёбер является множество
а множеством его рёбер является множество 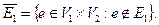
б) Объединением графов  и
и  при условии, что
при условии, что 
 называется граф
называется граф  множеством вершин которого является множество
множеством вершин которого является множество  а множеством его рёбер является множество
а множеством его рёбер является множество 
в) Пересечением графов  и
и  называется граф
называется граф 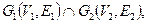 множеством вершин которого является множество
множеством вершин которого является множество  а множеством его рёбер является множество
а множеством его рёбер является множество 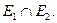
г) Суммой по модулю два графов  и
и  при условии, что
при условии, что 
 называется граф
называется граф  множеством вершин которого является множество
множеством вершин которого является множество  а множеством его рёбер – множество
а множеством его рёбер – множество  Т. е. этот граф не имеет изолированных вершин и состоит только из рёбер, присутствующих либо в первом графе, либо во втором графе, но не в обоих графах одновременно.
Т. е. этот граф не имеет изолированных вершин и состоит только из рёбер, присутствующих либо в первом графе, либо во втором графе, но не в обоих графах одновременно.


Дата добавления: 2015-08-27; просмотров: 40 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Изоморфизм графов | | | Аналитический способ задания графов |