Постановка задачи

В рамках данной работы было необходимо разработать приложение для операционной системы Android, позволяющее выводить нильпотентные матрицы третьего и группировать их по степеням.
Также пользователь должен иметь возможность сохранять результаты вычислений в файл.
В качестве языка для разработки был выбран язык Java, как наиболее удобный для разработки под эту операционную систему. В качестве среды разработки была выбрана среда Eclipseс установленным AndroidSDK.
Тестирование приложения осуществлялось на планшетном компьютере AsusTransformerPadInfinity, интерфейс также разрабатывался для комфортной работы на этом устройстве.

3 Нильпотентные матрицы
Нильпотентные матрицы играют важную роль в моделировании управления большими системами. Нильпотентность означает синхронизируемость и помагает в решении классических задач поддержания безопасности сложных систем.

3.1 Нильпотентный оператор
Определение. Линейный оператор пространства называется нильпотентным, если его минимальный многочлен имеет вид , - показатель нильпотентности.
Таким образом из определения следует, что если - показатель нильпотентности, то , но . Однако для некоторых окажется, что 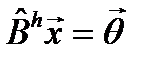при .
Все собственные значения нильпотентного оператора . Действительно, если - собственный вектор оператора , то .
Поэтому
Пусть - нильпотентный оператор и для вектора и некоторого выполнены условия ,тогда векторы линейно независимы.
Определение. Подпространством циклическим относительно нильпотентного оператора называется линейная оболочка векторов , если . Говорят, что циклическое подпространство порождается вектором . Векторы линейно независимы и образуют базис в циклическом подпространстве, называемым циклическим базисом.
Лемма (О показателе нильпотентности). Показатель нильпотентности оператора равен кратности корня в минимальном многочлене.
Теорема. (О нильпотентном операторе) Если оператор нильпотентный, то найдется базис, в котором матрица оператора будет иметь блочно-диагональный вид , где 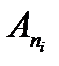имеет вид 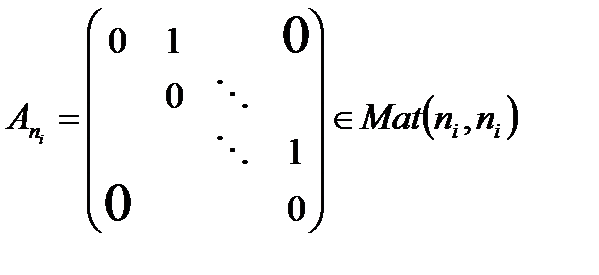. Такой вид оператора единственен с точность до перестановки блоков 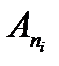(клеток одного размера всегда постоянное количество). Такая форма оператора называется нормальной.

3.2 Нильпотентная матрица.
Нильпотентная матрица — матрица, являющаяся нильпотентным элементом относительно умножения, то есть матрица P, для которой существует целое число n такое, что выполняется условие =O, где O - нулевая матрица.
Если в поле комплексных чисел все собственные значения матрицы равны нулю, то матрица нильпотентна.
Свойство. det =1, E - единичная, N - нильпотентная (квадратная матрица со свойством =O;
Примеры:

· матрица нильпотентна, так как =O;

· матрица нильпотентна, так как =O;

· матрица нильпотентна, так как =O

4 Описание конечного продукта
Приложение устанавливается как обычное приложение Android, после чего появляется в списке приложений. При запуске появляется главное окно программы, из которого и производятся все необходимые действия с матрицами:

Рисунок 5. Главное окно программы

При нажатии на кнопку "Эксперимент" попадаем в другое окно, и, прежде чем произвести вычисление, нужно сначала задать размерность матрицы. Каждая из них выводится в одной из соответствующих групп. В первую очередь выводим матрицы, у которых квадрат равен нулю, затем те, у которых куб равен нулю, потом выводим матрицы, у которых куб не равен нулю.
Например получаем: =O, количество матриц: 22
=O, количество матриц: 42
≠O, количество матриц: 448

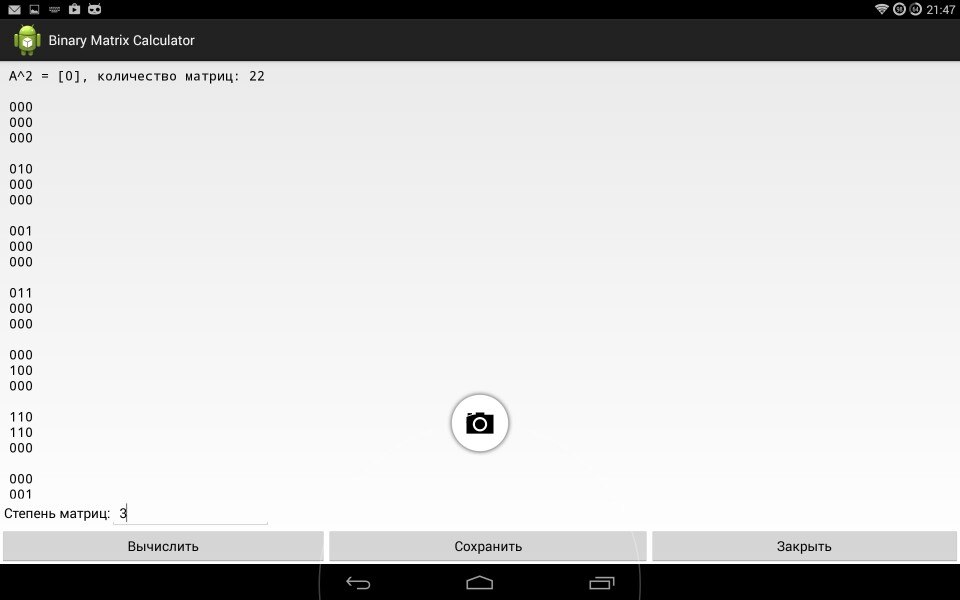
Рисунок 6. 22 нильпотентные матрицы =O, при размерности 3х3

Рисунок 7. 316 нильпотентных матриц =O, при размерности 4х4

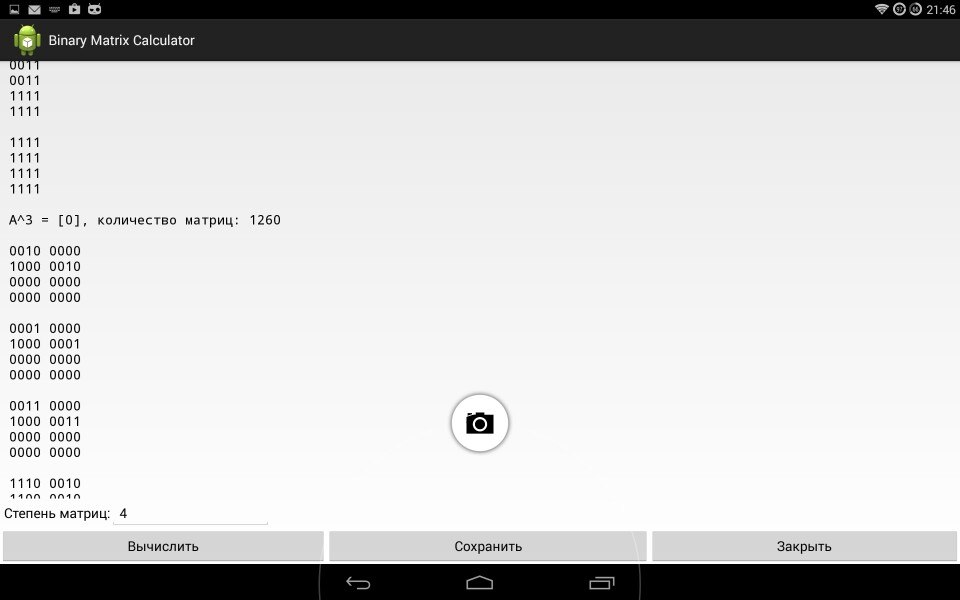
Рисунок 8. 1260 нильпотентных матриц =O, при размерности 4х4

Рисунок 9. 448 нильпотентных матриц ≠O, при размерности 3х3

В случае, когда производится некорректная операция (например, перемножение матриц несовпадающих размерностей), программа показывает всплывающее сообщение с объяснением ошибки.
В случае, когда производится некорректная операция (например, некорректная степень), программа показывает всплывающее сообщение с объяснением ошибки.

Рисунок 10. всплывающее окно с ошибкой

Дата добавления: 2015-08-26