Читайте также:
|
Уравнение кинематического баланса цепи главного движения станка модели 1К62 (см. п/п. 3.4.3 и рис. 3.11) для правого вращения может быть представлено в следующем виде:
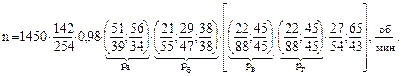
1) По кинематической схеме и уравнению кинематического баланса можно заключить, что коробка скоростей (КС) имеет сложенную структуру на 30 вариантов частот вращения шпинделя, состоящую из двух кинематических цепей передач, одна из которых (обозначим в соответствии с изложенным в п/п. 3.9.6.4 zo·zт) предназначена для получения низших, а другая (zo·zc) – высших скоростей привода;
2) Решение уравнения кинематического баланса показывает, что КС обеспечивает следующие частоты вращения шпинделя (рассчитанные значения частот округлены до стандартных значений чисел геометрического ряда), об/мин:
| 12,5 – | 16 – | 20 – | 25 – | 31,5 – | 40 – |
| 50 – | 63 – | 80 – | 100 – | 125 – | 160 – |
| к а ж д а я ч а с т о та п о л у ч а е т с я д в а ж д ы | |||||
| 200 – | 250 – | 315 – | 400 – | 500 – | 630 – дважды |
| 800 – | 1000 – | 1250 – | 1600 – |
Как видно, фактическое число различных значений частот вращения шпинделя (zф = 23) меньше структурного числа вариантов (z = 30), так как несколько частот (7) повторяется. Таким образом, в КС имеет место перекрытие части ступеней скорости;
3) Знаменатель геометрического ряда частот вращения шпинделя равен:
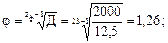
4) Знаменатели рядов передаточных отношений в группах передач pа, pб, pв, pг, составляющих общую и тихоходную части привода zo·zт, и порядок переключения групп будут следующими:
| Группы | Взаимосвязь i в группах передач | Значения знаменателей групп | Порядок переключения групп | Характеристики групп |
| pа=2 |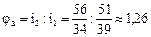 
| 
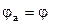
| pо (основная гр.) | xо = 1 |
| pб=3 |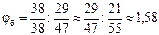 
| 
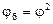
| pI (I множительн.) | xI = 2 |
| pв=2 |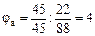 
| 
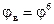
| pII (II множительн.) | xII = 6 |
| pг=2 |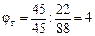 
| 
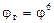
| pIII (III множительн.) | xIII = 6 |
Развёрнутая структурная формула кинематической цепи для низших скоростей привода будет: zo·zт= pа·pб·pв·pг= 2(1)·3(2)·2(6)·2(6);
5) Как видно, характеристика последней множительной группы (6) меньше расчётного значения (12) и цепь zo·zт является структурой с перекрытием, которая обеспечивает
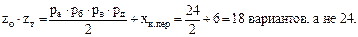
Кинематической цепью для высших скоростей обеспечивается zo·zc= 6 вариантов.
Однако же суммарное число различных частот вращения шпинделя не 18+6=24, а 23. Это имеет место потому, что первая цепь обеспечивает частоты n1-n18, а вторая – n18-n23, а не n19-n24, т.е. ещё две частоты (630 об/мин) повторяются.
Общая часть слагаемых структур – zo= 6 = 2(1)·3(2);
6) На основании полученных данных можно построить структурную сетку привода (рис. У.16);
7) Сложенная структура с перекрытием привода главного движения станка модели 1К62 обеспечивает диапазон регулирования при zф = 23 и 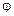 = 1,26 Д = 2000/12,5 = 160.
Нормальная множительная структура на 24 варианта обеспечивала бы Д = 1,1224–1 = 14 (т.к. 2(1)·3(2)·2(6)·2(12) = 24 и  ).
| 
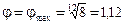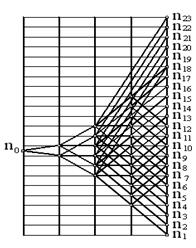Рис. У.16. Структурная сетка привода
главного движения станка модели 1К62
|
Дата добавления: 2015-08-26; просмотров: 347 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Бесступенчатое регулирование скорости | | | Особенности расчета и проектирования коробок подач |