Угол между двумя прямыми. Уравнение биссектрисы угла между двумя прямыми.

Углом между прямыми A и B называется угол, на который надо повернуть первую прямую A вокруг точки пересечения этих прямых против движения часовой стрелки до совпадения ее со второй прямой B. Если две прямые заданы уравнениями с угловым коэффициентом

y₁ = k ₁ x + B ₁,

y₂ = k ₂ x + B ₂, (1)

то угол между ними θ определяется по формуле

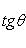
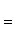
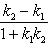
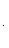(2)

Если уравнения прямой заданы в общем виде

A ₁ x + B ₁ y + C ₁ = 0,

A ₂ x + B ₂ y + C ₂ = 0, (3)

угол между ними определяется по формуле

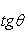
(4)

Условия параллельности двух прямых:

а) Если прямые заданы уравнениями (1) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:

k ₁ = k ₂. (5)

б) Для случая, когда прямые заданы уравнениями в общем виде (3), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.

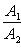
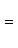
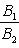
(6)

Условия перпендикулярности двух прямых:

а) В случае, когда прямые заданы уравнениями (1) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратные по величине и противоположны по знаку, т. е.

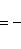
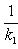
(7)

Это условие может быть записано также в виде

k ₁ k ₂ = -1. (8)

б) Если уравнения прямых заданы в общем виде (3), то условие их перпендикулярности (необходимое и достаточное) заключается в выполнении равенства

A ₁ A ₂ + B ₁ B ₂ = 0. (9)

Координаты точки пересечения двух прямых находят, решая систему уравнений (3). Прямые (3) пересекаются в том и только в том случае, когда

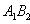
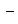
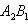
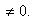
Уравнения биссектрис углов между прямыми Ax + By + C = 0 и A ₁ x + B ₁ y + C ₁ = 0:

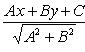
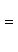
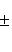
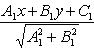
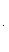
Уравнение пучка прямых, проходящих через точку пересечения двух данных прямых:

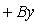
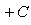
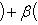
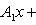
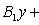
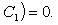(1)

Можно положить α=1, исключив этим из пучка вторую из данных прямых.

Дата добавления: 2015-08-17