Напряжение

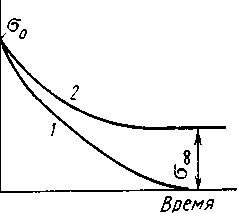
Рисунок 2.1 – Релаксация напряжения в линейном (1) и пространственно сшитом (2) эластомере

Через определен­ный промежуток времени происходит перегруппировка всех напря­женных узлов флуктуационной сетки, что дает возможность

клуб­кам макромолекул перейти в прежнее свернутое статистически наиболее вероятное состояние. В этот момент напряжение в образце падает до нуля, а структура образца становится такой же, как и до растяжения. Но сама деформация растяжения не измени­лась – она по-прежнему равна 100%. Это может произойти только в том случае, если в процессе сворачивания клубков и перегруппировки узлов флуктуационной сетки клубки одновременно смеща­лись относительно друг друга. Такой процесс есть процесс течения макромолекул. Теперь после освобождения-образца из зажимов динамометра он более не сократится Эластическая деформация в 100%, которой был подвергнут образец вначале вся перешла в де­формацию течения.

Чем более полярен полимер, тем более пологой оказывается кривая релаксации — медленнее падает напряжение.

Если эластомер пространственно сшит (вулканизован), т. е. на ряду

с флуктуационной сеткой в нем образовалась сетка химических связей то эта последняя практически не релаксирует. Правильнее сказать, что она релаксирует много медленнее, чем флуктационная сетка. В пространственно-сшитом образце напряжения релаксируют до тех пор, пока все они не сосредоточатся на узлах химической сетки. При этом все узлы флуктационной сетки оказы­ваются разгруженными. Напряжение в образце достигает предела (кривая 2 рис. 2.1). Химические связи препятствуют необратимому перемещению клубков молекул, но не препятствуют перемещению сегментов. Если образец освободить из зажимов ди­намометра, то он с течением времени полностью вос­становит свои первоначальные размеры и только тогда напряжение в нем упадет до нуля.

В опыте по релаксации напряжения в растяну­том образце, как мы видели, эластическая обрати­мая деформация со временем переходит в вязкоте- кучую необратимую. Полностью обратимая дефор­мация развивается в идеально упругой стальной пружине, а полностью необратимая деформация развивается при нагружении поршня, помещенного в идеальную жидкость. По

следовательное соедине­ние пружины и поршня является простейшей мо­делью вязкоупругого тела (рис. 2.2). Эта модель носит название модели Максвелла (по имени ее соз­дателя).

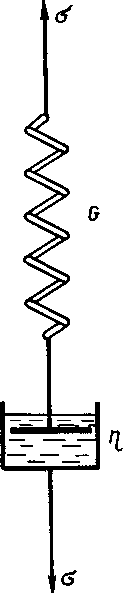
Рисунок 2.2 - Модель Максвелла

Процесс релаксации напряжения описывается уравнением Максвелла:

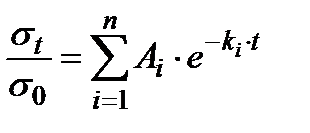
где σ_t и σ₀ – напряжение растяжения в образце в момент времени t и начальный момент соответственно;

Ai – коэффициент, учитывающий долю i-го процесса релаксации;

ki – константа скорости i-го процесса релаксации.

2.2 Ползучесть

Для изучения релаксационных явлений образец быстро нагружают и следят за ходом де­формации растяжения под действием приложенной нагрузки. При этом слож­ность состоит в том, что поперечное се­чение образца со временем уменьшается и таким образом одна и та же нагрузка вызывает в расчете на постоянно умень­шающуюся площадь поперечного сече­ния все

возрастающее напряжение. Су­ществует немало остроумных способов уменьшения действующей силы (груза) по мере растяжения образца, так чтобы сохранить неизменным во времени действующее напряжение. В конечном счете ползучесть осуществляется в режиме σ=const, ε =f(t). На рисунке 2.3 показана типичная кривая ползучести линейного полимера (кривая 1).

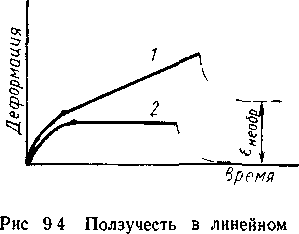
Рисунок 2.3 – Ползучесть в линейном (1) и пространственном полимере.

Под действием нагрузки макромолекулярные клубки развертываются, часть сегментов перемещается, ориентируясь в направлении действия силы. Перемещение сегментов приводит также к смещению клубков относительно друг друга. Таким образом, с самого момента нагружения образца в нем развиваются одновременно и обра­тимая высокоэластическая дефор­мация, и деформация необратимая вязкотекучая.

Если после некоторого времени образец разгрузить, то он частично сократится за счет свертывания клубков макромолекул. Это и будет величина высокоэластической де формации, развившейся к моменту разгрузки

Однако полного сокращения не происходит, сохраняется некоторая остаточная деформация, являющаяся истинно необратимой вязко текучей.

Под действием заданного напряжения клубки макромолекул развернутся тем больше, чем меньше их упругость. Возникшая высокоэластическая деформация далее остается неизменной. Перемещением клубков относительно друг друга течение не прекратится вязкотекучая деформация будет нарастать во времени с постоянной скоростью. Поэтому кривая ползучести делится на два участка начальный криволинейный, когда развиваются оба типа деформации и линейный участок когда накапливается только вязкотекучая деформация. Строго говоря, наличие линейного участка характерно только для полимера с одним временем релаксации. Для реального полимера можно наблюдать участок кривой кажущийся линейным за время наблюдения, но в действтельностни обусловленный различными типами молекулярных перемещений с очень большими временами релаксации.

На том же рис. 2.3приведена кривая ползучести идеального сетчатого эластомера (кривая 2) в нем не возникает необратимая деформация из за наличия прочных химических связей исключающих взаимное перемещение макромолекул. Эластическая деформация осуществляется лишь в той мере в какой позволяет сетка химических связей ползучесть развивается, достигая предела. После разгрузки образец сокращается до первоначальных размеров.

Основная особенность кривой ползучести — наличие участка замедленного развития упругой деформации. В реальном полимере упругая деформация развивается не мгновенно как в пружине, а замедленно так как перемещение сегментов тормозится вязким сопротивлением среды.

Указанная особенность — наличие замедленной упругости (высокоэластичности) — отображается моделью Кельвина — Фойхта рис. 2.4

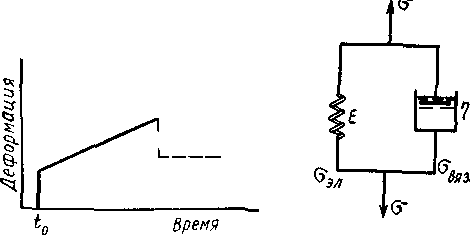
Рисунок 2.4 – Модель Кельвина - Фойхта

Здесь пружина и поршень соединены параллельно напряжения на них складываются 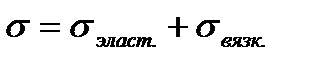. По закону Гука 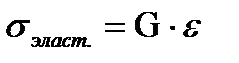, по закону вязкого

течения Ньютона 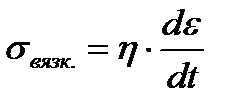. В результате 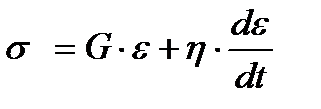, откуда после интегрирования получаем 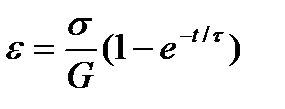. Это уравнение не предусматривает наличия необратимой деформации поэтому лучше всего моделирует ползучесть пространственно сшитого эластомера. Ползучесть линейного полимера хорошо описывается также объединенной механической моделью сочетающей модель Максвелла и модель Кельвина - Фойхта.

2.3 Релаксационные процессы в полимерах

В процессах релаксации участвуют различные структурные элементы полимера, каждый из которых имеет свои времена релаксации, лежащие в широком интервале — от 10^-12 с до многих лет. Релаксационные свойства полимеров зависят от типа и размера релаксирующих в данных условиях элементов структуры. Поэтому для полной характеристики полимеров не­обходимо рассматривать сумму всех релаксационных процес­сов, образующих так называемый релаксационный спектр. Эти спектры получают или статическими методами (релаксация напряжения) или динамическими (механические или диэлект­рические потери).

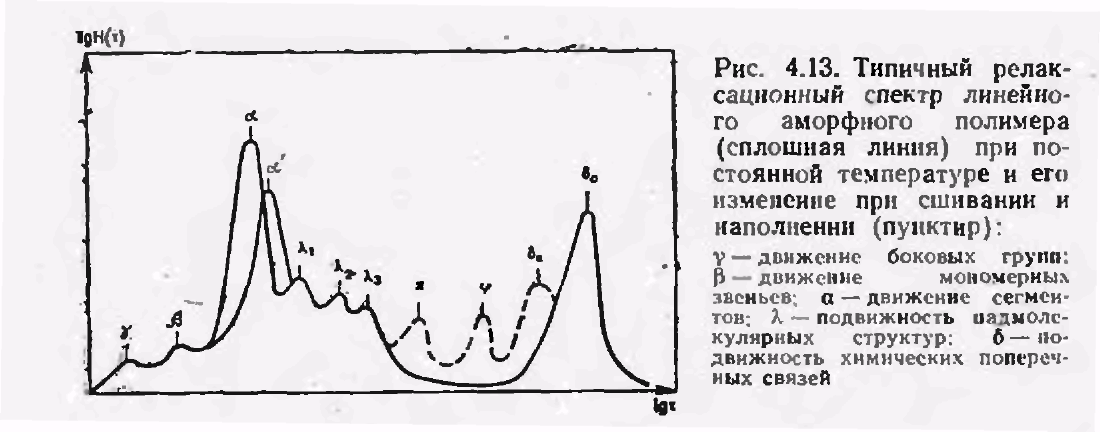
Рисунок 2.5 – Типичный релаксационный спектр линейного аморфного полимера (сплошная линия) при постоянной температуре и его изменение при сшивании и наполнении (пунктир): γ – движение боковых групп; β – движение мономерных звеньев; α – движение сегментов; λ – подвижность надмолекулярных структур; δ – подвижность химических поперечных связей

На рисунке 2.5 приведен типичный спектр вре­мен релаксации линейного полимера. Максимумы на релакса­ционном спектре соответствуют временам релаксации τ_i* каждой релаксируюшей единицы при постоянной температуре. Каждое дискретное время, характеризующее данный переход, зависит от температуры и снижается при ее повышении вслед­ствие увеличения подвижности элементов структуры:

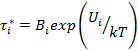
где В_i — константа, зависящая от размеров структурного элемента; U_i — энергия активации i-й структурной единицы, равная высоте энергетического барьера, преодолеваемого при переходе структурного элемента из одного равновесного состояния в другое.

В общем случае процесс релаксации напряжения при заданной деформации описывается уравнением

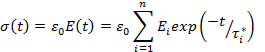
где σ(t) и E(t)—напряжения и модуль через время t при деформации ε₀; τ_i* — время релаксации i-й кинетической единицы; n — число кинетических единиц различных типов; E_i — коэффициент, соответствующий вкладу i-ой кинетической единицы в общий процесс релаксации.

Среднее значение времен релаксации всех структурных еди­ниц называется средним временем релаксации τ_ср*.

Неоднородность структуры полимера, введение наполните­лей и других компонентов, соединение макромолекул друг с другом, например при образовании пространственной сетки в процессе вулканизации каучуков, приводит к увеличению числа структурных элементов, влияющих на релаксационные процес­сы. В макромолекуле, содержащей разные по структуре и раз­мерам боковые группы, вместо одного максимума γ-процесса имеется несколько (γ₁, γ₂ и т д) с низкой энергией активации (10—20 кДж/моль). Для гомополимера характерен один β-переход, а для блок-сополимера уже два — β₁ и β₂. В кристалли­ческих полимерах одна и та же структурная единица обладает различной подвижностью в аморфной и кристаллической фа­зах, соответственно наблюдаются два перехода β и β₁ харак­терные для аморфной и кристаллической структуры. Например, в спектре полиэтилена высокой плотности проявляются β- и β₁-переходы при 150 и 250 К и частоте 1000 Гц. Очень часто вмес­то одного а- и λ-максимумов появляется несколько, что обус­ловлено различной подвижностью сегментов (а-переход) или надмолекулярных структур (λ-переход). Например, в кристал­лических полимерах (полиэтилене) существует даже три мак­симума - а, а₁ и а₂, обусловленные сегментальной подвиж­ностью в аморфной фазе, переходных аморфно-кристалличес­ких межфазных слоях 'и аморфных участках лучей сферолитов.

λ-Переходы, обусловленные подвижностью надмолекуляр­ных структур, относятся к медленным релаксационным процес­сам и связаны с наличием физической сетки. В некоторых по­лимерах могут существовать физические узлы различной природы, например в бутадиен-нитрильных эластомерах прояв­ляется так называемый π-процесс релаксации, обусловленный диполь-дипольным взаимодействием групп 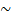CN---NC~ (при 363 К).

При образовании водородных связей в спектре обнаруживается переход, аналогичный π-переходу, но при более высокой температуре. Переходы, обусловленные ре­лаксацией химических связей между молекулами (δ), также могут проявляться в виде нескольких максимумов, если суще­ствуют связи различной энергии. Так, в серных резинах наря­ду с переходом δ_с-с имеет место переход δ_s, обусловленный подвижностью (т. е. разрывом) химических серных связей.

В наполненных полимерах вместо одного а-перехода появ­ляется еще один — а', обусловленный подвижностью сегмен­тов макромолекул, адсорбированных поверхностью наполнителя, а также φ-переход, который связывают с подвижностью частиц наполнителя в среде полимера. В таблице 2.1 приведены характеристики релаксационных процессов в резинах на осно­ве наполненного сополимера бутадиена со стиролом.

Таблица 2.1- Характеристики релаксационных процессов в резине на основе сополимера бутадиена и стирола (70:30) с 20% технического углерода П-234

Релаксационный процесс	Характерное время релаксации при 293К, τi,с	Энергия активации Ui,кДж/моль	Константа Bi­, с	Объем кинетической единицы Vi, см^3	Линейные размеры кинетической единицы, нм
β	1*10^-8		5*10^-13	2*10^-22	0,5
α	6*10^-6		5*10^-12	1*10^-21	3-4
α’	1,5		4,8*10^-12	1*10^-21	3-4
λ	1,6*10^2		2,6*10^-8	2,0*10^-17
2,1*10^3		3,4*10^-6	4*10^-16
4,3*10^4		6,9*10^-6	1,6*10^-14
φ	2*10^5		1,6*10^-8	0,9*10^-17
δ	4*10^9		2*10^-13	≈10^-23	0,2-0,3

Вклад каждого релаксационного процесса зависит от его характерам условий проявления. Деформация полимера в стеклообразном состоянии при Т<Т_С сопровождается релаксационными β- и γ-переходами. Энергия активации этих переходов намного мень­ше, и поэтому высота их пиков намного ниже, чем в случае α-перехода. Они оказывают существенное влияние на механи­ческие свойства полимеров в стеклообразном состоянии. При растяжении в высокоэластнческом состоянии наибольшее влия­ние на релаксацию оказывают не γ- и β-, α α-, α'-, λ-, δ- и φ-переходы, т. е. процессы ориентации сегментов (τ=10^-6 — 10^-3с), перегруппировки надмолекулярных структур (τ=10²— 10⁴ с), перегруппировки поперечных химических связей и связей в цепях (τ=10⁷—10⁹с) и др.

Однако влияние этих факторов на скорость релаксацион­ных процессов зависит от продолжительности действия силы. Как уже упоминалось, вероятность проявления гибкости мак­ромолекулой зависит от соотношения времени действия силы и времени, необходимого для изменения конформации. Послед­нее есть не что иное, как время релаксации τ*, поэтому можно считать, что реакция полимера на механическое воздействие определяется соотношением между временем релаксации и временем деформации τ*/t (рисунок 2.7). Если τ*/t 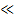1, то систе­ма очень быстро релаксирует и приходит в равновесное состоя­ние. Это условие может быть реализовано или при очень ма­лых значениях τ*, или при очень высоких значениях t. Для полимеров этот случай имеет место при высоких температурах (τ* снижается) или очень низких скоростях воздействия. При τ*/t 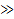1 релаксация протекает очень медленно, что может быть следствием или высоких значений τ* (система малоподвижна, например в стеклообразном или кристаллическом состояниях), или высоких скоростей механического воздействия. При τ*/t→1 релаксационные процессы развиваются за какой-то опреде­ленный промежуток времени и оказывают наибольшее влияние на свойства материала. Таким образом, релаксационные явле­ния проявляются для всех рассмотренных физических состоя­ний — стеклообразного, вязкотекучего и высокоэластического, но в наибольшей степени релаксация характерна для высокоэластического состояния.

Если сопоставить влияние температуры и времени действия силы, то можно отметить, что отношение τ*/t снижается либо при повышении температуры (τ* уменьшается), либо при уве­личении t, т. е. существует эквивалентность влияния времени и температуры. Этот принцип получил название принципа температурно-временной суперпозиции (ТВС). Любая релаксационная характеристика при изменений температуры от Т до Т^’ из­меняется на величину K, равную

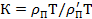
(ρ_п и ρ_п' — плотность полимера при Т и Т').

На основании принципа ТВС, зная температурные зависи­мости какого-либо показателя, отражающего релаксационные свойства в узком интервале скоростей воздействия, можно предсказать, как будет изменяться это свойство при любой за­данной температуре при изменении скорости воздействия. На рисунке 2.7 показано использование принципа ТВС для гипо­тетического полимера при релаксации напряжения. Кривая при определенной температуре, например при 273 К, выбирается в качестве отсчетной; эта температура называется приведенной Т_пр. Затем все кривые сдвигаются вдоль логарифмической шкалы времени до их наложения. Кривые при Т>Т_пр сдвигаются вправо, а кривые при Т<Т_пр влево. Обобщенная кривая при Т_пр охватывает значительно больший период времени, чем экс­периментальные данные. Расстояние, на которое сдвигались со­седние кривые вдоль оси абсцисс, называется фактором приве­дения а_Т.

Температурная зависимость фактора приведения а_Т описывается уравнением Вильямса — Ландела — Ферри (ВЛФ):

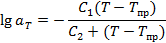
(С₁ и С₂—эмпирические константы).

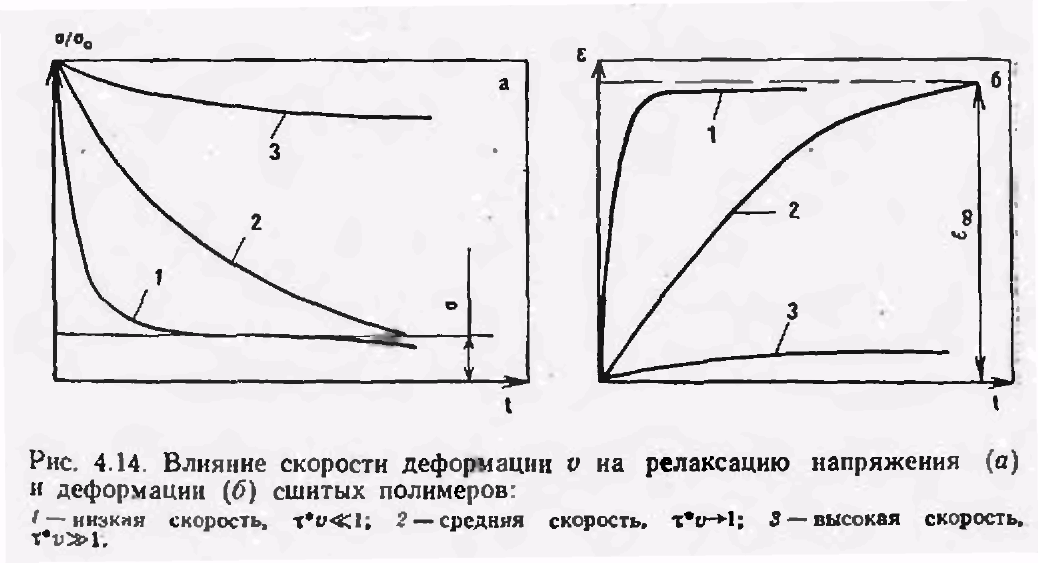
Рисунок 2.6 – Влияние скорости деформации υ на релаксацию напряжения (а) и деформацию (б) сшитых полимеров: 1 – низкая скорость τ^*υ 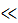1; 2 – средняя скорость τ^*υ→1; 3 – высокая скорость τ^*υ 1

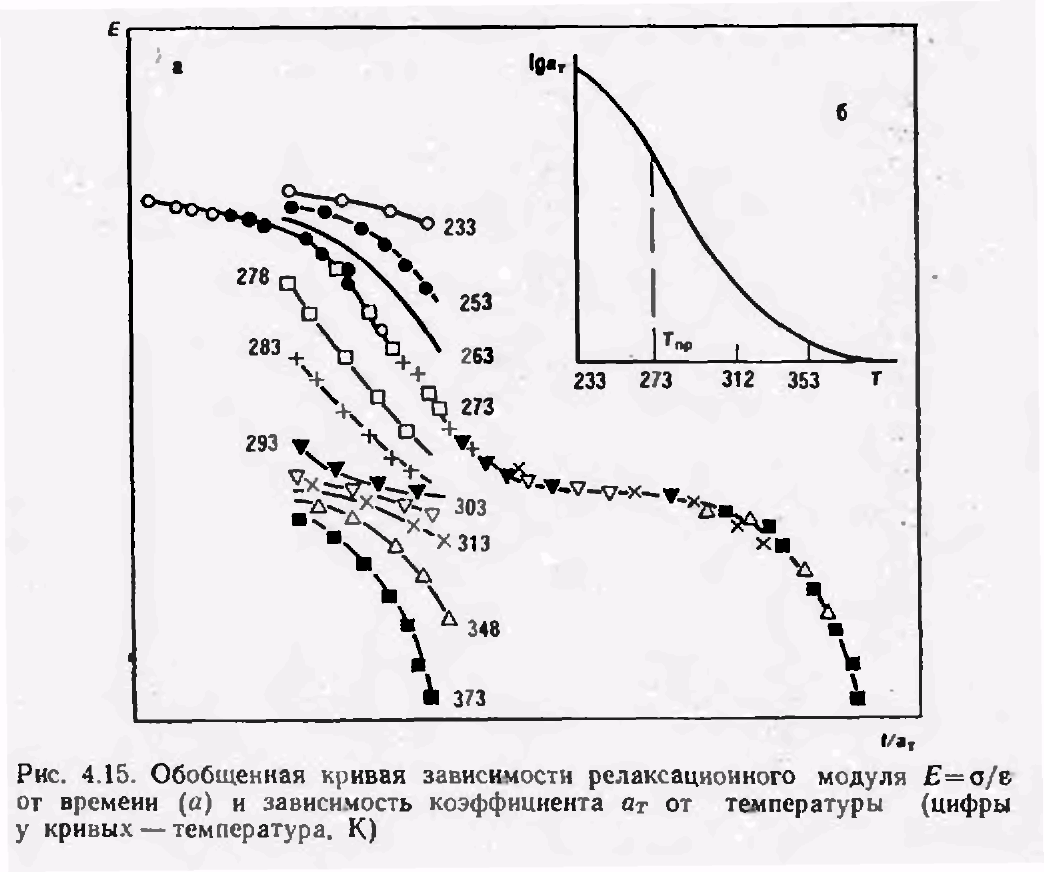
Рисунок 2.7 – Обобщенная кривая зависимости релаксационного модуля Е=σ/ε от времени (а) и зависимость коэффициента а_Т от температуры (цифры у кривых – температура, К)

В качестве температуры приведения Т_пр часто выбирают Т_с. В этом случае для большинства аморфных полимеров а_Т примерно одинаково и равно

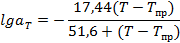
Если же за Т_пр выбирается другая температура, то константы С₁ и С₂ будут иметь другие значения.

2.4 Различные типы релаксационных переходов в полимерах

Релаксационные явления в значительной степени определяют протекание физических и химических процессов в полимерах. Полимеры — сложные многоуровневые системы, со­стоящие из структурных элементов (кинетических единиц) раз­личной природы (атомов, боковых и концевых групп, звеньев макромолекул, свободных и связанных сегментов, элементов надсегментальной и надмолекулярной структуры, физических и химических узлов сетки, частиц наполнителя и т. д.). Это при­водит к большому разнообразию форм молекулярной подвиж­ности и соответствующих им релаксационных процессов, кото­рые наблюдаются при действии на полимер механических, электрических или магнитных полей. При этом наиболее уни­версальным воздействием, позволяющим получить полную ин­формацию о молекулярной подвижности и процессах релакса­ции в полимерах, является механическое воздействие. Элект­рические и магнитные поля могут вызвать не все релаксацион­ные переходы, так как электрическое поле действует только на элементы, обладающие дипольным моментом, а магнитное по­ле — на элементы, обладающие магнитным моментом.

Релаксационные процессы (переходы) связаны с различны­ми формами теплового движения в полимере, характеризуемо­го спектром молекулярной подвижности структурных элемен­тов. Этому спектру соответствуют

кретные τ₁, τ₂,… τ_n и не­прерывные Н(τ) спектры времен релаксации (рисунок 2.9). Дис­кретному спектру τ_i соответствует п релаксационных перехо­дов, проявляющихся в виде максимумов на непрерывном спект­ре Н(τ). Максимумы на спектре внутреннего трения χ(Т) со­ответствуют дискретному спектру температур Т_i релаксацион­ных переходов (i=1, 2,..., n) (рисунок 2.10).

Из температурных зависимостей τ_i и частотных зависимо­стей Т_i можно получить сведения о размерах кинетических единиц, участвующих в каждом релаксационном процессе, и осо­бенностях их внутреннего строения, а также сведения об энер­гиях активации процессов, зависящих от характера взаимодей­ствия кинетических единиц и прочности их сцепления.

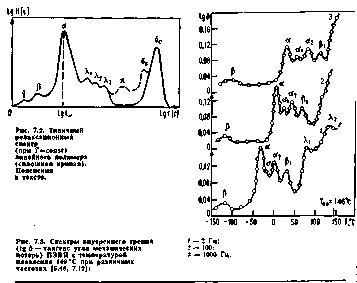
Рисунок 2.8 – Типичный релаксационный спектр

Рисунок 2.9 – Спектр внутреннего трения

В связи с этим релаксационная спектрометрия выступает как структурный метод, позволяющий выявить все возможные ре­лаксационные переходы, характерные для данного полимерно­го материала, и выяснить их природу, т. е. природу структур­ных элементов, участвующих в переходе. Поскольку

дискрет­ный спектр времен релаксации дает информацию о вязкоупругих свойствах полимера, релаксационная спектрометрия является основой для методов прогнозирования.

Релаксационным процессам соответствуют максимумы как на спектрах внутреннего трения χ(Т) или χ(ω), так и на спект­рах времен релаксации Н(τ). Эти спектры могут быть получе­ны как квазистатическими методами (релаксация напряже­ния), так и динамическими методами (механические потерн, диэлектрические потери и т. д.).

Максимумы на релаксационных спектрах (см. рисунок 2.8) со­ответствуют временам релаксации дискретного спектра τ_i при заданной температуре Т=const, а максимумы на спектрах внутреннего трения (см. рисунок 2.9) соответствуют дискретным температурам релаксационных переходов Ti при заданной частоте деформации ω = const или дискретным частотам переходов ω_i при заданной температуре T=const. По частотным зависи­мостям температур Ti и температурным зависимостям частот ω_i могут быть рассчитаны времена релаксации τ_i. В целом дискретный спектр времен релаксации характеризуется време­нами T₁, T₂,..., Т_n и вкладами E₁,E₂,…E_n отдельных релакса­ционных процессов. При этом доля каждого вклада не зави­сит от температуры.

Каждое дискретное время, характеризующее данный ре­лаксационный переход, зависит от температуры по известному уравнению Больцмана — Аррениуса:

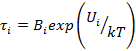
где Ui — энергия активации i-того процесса, зависящая от сил взаимодейст­вия кинетических единиц, а k—коэффициент, зависящий от их размеров.

Энергии активации различны для разных релаксационных переходов, но практически для всех наблюдаемых релаксаци­онных процессов не зависят от температуры в пределах точно­сти измерений, за исключением α-процесса (стеклование).

Экспериментальные данные по дискретному релаксационно­му спектру могут быть представлены в координатах lg τ_i-1/T в виде семейства прямых, как это следует из уравнения. Тогда из наклонов прямых находятся Ui, а из отрезков, отсе­каемых на оси 1/T=0,— коэффициент Bi. Независимым мето­дом эти постоянные можно определить из данных спектра внут­реннего трения (динамический метод) по зависимости темпе­ратуры перехода Ti от частоты деформации ω = 2πν, где ν — линейная частота. Так, температуре перехода соответствует из­вестное условие:

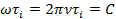
где С – безразмерная константа, С≈1 для мелкомасштабных движений (атомы, группы атомов в γ-, β-, δ-процессах) и С≈10 для сегментов и более крупных единиц.

Учитывая первое уравнение, получим:

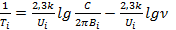
Отложив экспериментальные данные в координатах 1/T_i—Igν, находят значения Ui и Bi, а затем вычисляют τ_i. Только в том случае, когда оба метода дают совпадающие результаты по числу релаксационных переходов n и по величинам τ_i, полученный дискретный спектр релаксаци­онных переходов считается надежным и отражающим струк­турные особенности полимера.

Релаксационным переходам в полимерах посвящено много обстоятельных исследований, результаты которых суммирова­ны в монографиях. Работы последних лет привели к четкой классификации релаксационных переходов в аморфных и кристаллических поли­мерах. Все релаксационные переходы можно разбить на не­сколько групп, каждая из которых характеризуется молекуляр­ной подвижностью одного и того же структурного элемента.

К первой группе относятся мелкомасштабные релаксацион­ные процессы, связанные с подвижностью боковых привесков в макромолекулах (γ-группа). Потеря подвижности (колеба­тельно-вращательных движений) этих кинетических единиц происходит при низких температурах (обычно ниже 200 К). Энергия активации мала (10—20 кДж/моль), а коэффициент В_i в уравнении примерно равен 10^-13 с. Разные по структуре и размерам боковые группы в линейных полимерах отвечают γ₁-, γ₂- релаксационным переходам и т.д. Эти пере­ходы обнаруживаются по механическим и диэлектрическим потерям при высоких частотах, так как времена релаксации τ_i для этих процессов малы (10^-9—10^-10 с при 300 К), а частоты велики (с=1 и ν≈10^e Гц). По терминологии, принятой для диэлектрической релаксации в по­лимерах, процессы этой группы называются дипольно-групповыми γ-процессами.

Ко второй группе относятся мелкомасштабные процессы, связанные с подвижностью малых участков полимерной цепи — звеньев (β-группа). Процессы этой группы протекают в аморф­ной фазе полимера, находящегося в стеклообразном состоянии, когда сегментальная подвижность еще заморожена. На рисунке 2.9 виден β-переход для полиэтилена (T_β= - 146°С) при ν=l Гц. С точки зрения реакции на действие электрических переменных полей (диэлектрическая релаксация), β-процесс— это локаль­ное движение полярных групп, связанное с изгибными колеба­ниями малых групп в основной цепи (дипольно-групповые β-процессы). Для полиэтилена В_i= 1,6- 10^-13 с, U_i = 30 кДж/моль и процесс связывается с подвижностью групп СН₂ в цепи полиэтилена. Так как B_i~v_i — объему кинетической единицы, то для ПЭ u_i≈(2-4)10^-20 мм³. Для разных поли­меров B_i различаются мало, но энергии активации могут при­нимать значения до 80 кДж/моль.

Таким образом, процессы γ- и β-групп относятся к мелко­масштабным релаксационным процессам. Если полимерная цепь имеет боковые группы одного типа, то наблюдается один γ-процесс, если двух типов, то два γ-процесса. Для аморфного гомополимера наблюдается один β-переход, а для блок-сопо­лимера— два перехода. В кристаллических полимерах одна н та же

кинетическая единица находится в разных структурных условиях. Например, группы СН₂ по-разному проявляют свою тепловую подвижность в аморфной и кристаллической фазах полиэтилена. Соответственно наблюдаются β-, β₁-переходы (см. рисунок 2.9). Для обоих переходов одинаковы коэффициенты B_i = 1,6*10^-13 с, но различны энергии активации (30 и 68 кДж/моль).

К третьей группе относятся α-переходы, кинетической еди­ницей которых является сегмент с B_i =5*10^-12 с для гибкоцепных полимеров. Это значение B_i соответствует объему сегмента V_i≈10^-13 мм³. В аморфных полимерах наблюдается один α-переход (см. рисунок 2.9), ответственный за стеклование поли­мера; если полимер наполнен активным наполнителем, то по­является еще один— α^’-процесс с тем же значением B_i, но с энер­гией активации большей, чем для α-процесса. Например, для изопренового эластомера СКИ-3 при 300 К U_a =33 кДж/моль, a U_a’ = 62-67 кДж/моль в зависимости от типа наполнителя; для бутадиен-стирольного эластомера СКС-30 АРКМ-15 при 300К U_a = 34 кДж/моль, a U_a’=71 кДж/моль.

В кристаллическом полимере (полиэтилене) обнаруживают­ся кроме а-перехода еше два перехода (см. рисунок 2.9) с тем же значением В_i = 5-10^-12 с. Это указывает на то, что α₁- и α₂-переходы также связаны с сегментальной подвиж­ностью, но сегмент находится в других структурных условиях. Основной «-переход ответственен за стеклование аморфной фа­зы полимера. Для ПЭ U_a=51,5 кДж/моль и характеризует сегментальную подвижность в аморфной фазе полимера. Пе­реходы α₁ и α₂ с U_ai =54,5 кДж/моль и U_α2=59 кДж/моль связаны с сегментальной подвижностью в переходных аморф­но-кристаллических межфазных слоях и в аморфных участках лучей сферолитов. В кристаллической фазе сегментальная по­движность не проявляется (U_α= 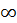). Для некристаллических гибкоцепных полимеров (эластомеров, пластмасс) характерные значения U_а=30 - 50 кДж/моль, а времена релаксации τ_a = = 10^-6 - 10^-3 с при З00К.

В переменных электрических полях наблюдаются аналогич­ные механическим диэлектрические дипольно-сегментальные потери, природа которых та же—сегментальная подвижность. В полимерных стеклах сегментальная подвижность играет важную роль, так как является причиной многих явлений (стеклование, вынужденная высокоэластичность, ползучесть, квазихрупкое разрушение, трещины «серебра» и т. д.). В кри­сталлических полимерах сегменты могут находиться в трех различных состояниях, а в наполненном аморфном полимере — в двух состояниях, что приводит к мультиплетности релакса­ционных спектров a-процесса релаксации. Основным при этом остается a-процесс, ответственный за стеклование. Его вклад, как можно судить по высоте максимумов на спектрах, суще­ственно больше, чем остальных процессов этой группы.

К четвертой группе относятся λ-процессы релаксации, на­блюдаемые

выше Т_с в зоне высокоэластического плато. Наблюдается как минимум три процесса: λ₁, λ₂, λ₃, но в сополимерах их может быть больше. Эти переходы обычно выражены слабо по сравнению с a-переходом и характеризу­ются тем, что коэффициенты В_i относительно велики (10^-8— 10^-5 с) —превышают В_i = 5*10^-12 с для сегментов на 3—6 порядков. При этом λ_i - процессы имеют одну и ту же энергию ак­тивации, совпадающую с энергией активации вязкого течения полимера, но различные В_i. Большие значения В_i указывают на то, что эти процессы связаны с подвижностью крупных структурных элементов, характерных для надсегментальных и надмолекулярных микроструктур, имеющих вид упорядоченных микрообластей (структурных объемных микроблоков, класте­ров).

В связи с этим структуру аморфных полимеров (по­лимерных стекол и эластомеров) можно представить состоя­щей из двух структурных частей: неупорядоченной части, вклю­чающей свободные сегменты и цепи (их подвижность проявля­ется в α-процессах), и упорядоченной части, распространенной по всему объему в виде упорядоченных микрообластей флуктуационного происхождения (структурных микроблоков глобулярного, складчатого и мицеллярного типов различных линей­ных размеров — от 10 до 100 нм).

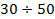Структурные микроблоки играют роль физических узлов молекулярной сетки, имеющих различные, относительно боль­шие времена жизни, которые соответствуют дискретным вре­менам λ_i процессов релаксации (τ_i= 10² 10⁺⁴ с при 300 К и U_λ = кДж/моль для различных линейных полимеров и объемом λ-микрообластей 10^-14-10^-15 мм³). Относительно низ­кие для структурных микроблоков, включающих тысячи и де­сятки тысяч «связанных» сегментов, значения U_λ, объясняют­ся тем, что распад и образование таких упорядоченных микрообластей происходит посегментально путем отрыва и прилипа­ния отдельных сегментов, аналогично испарению и конденса­ции капли жидкости, происходящим путем отрыва и прилипа­ния отдельных молекул.

Процессы λ-релаксации ответственны за медленные релак­сационные процессы в высокоэластическом состоянии, к кото­рым обычно относят ползучесть, медленную стадию релаксации; напряжения и вязкое течение, а процесс α-релаксации в этой же температурной области ответственен за быстрые релаксационные процессы. Во всех этих процессах, а также в процессе вытяжки и ориентации, основную роль играет релаксация физических узлов молекулярной сетки.

λ-процессы релаксации ответст­венны за механизм разрушения эластомеров. В полярных поли­мерах природа физических узлов молекулярной сетки может быть иной. Например, в бутадиен-нитрильных эластомерах между λ- и δ-процессами обнаруживается π-процесс релаксации (см. рисунок 2.8), связанный с распадом и рекомбинацией локальных физических поперечных связей, обусловленных диполь-дипольным взаимодействием между полимерными цепями CN…NC. Температура перехода этого процесса Т_л=90°С, энергия активации 90 кДж/моль, В_i= 10~¹⁰ с.

Пятая группа релаксационных переходов, следовательно, связана с подвижностью диполь-дипольных поперечных связей в полимерах.

Как следует из предыдущих глав, в твердых полимерах разрушение во многих случаях является следствием термофлуктуационного разрыва химических связей. Возникает вопрос, как связаны между собой процессы разрушения и релак­сационные процессы в полимерах. Обратимся к химическому процессу релаксации (δ-процесс). На релаксационном спектре (см. рисунок 2.9) представлен δ_c-процесс — процесс химической релаксации, связанный с распадом связей С—С. Сразу отме­тим, что указанный релаксационный спектр получен из изотерм релаксации напряжения при малых деформациях и напряже­ниях, далеких от разрывных. Поэтому энер­гия активации U_с должна быть близка к энергии активации процесса разрушения U_o и энергии термодеструк­ции E_D.

Дискретный спектр сшитого бутадиенметилстирольного эла­стомера СКМС-30 (рисунок 2.10) показывает, что вклад в релак­сацию напряжения б-процесса очень велик по сравнению с вкладом λ-процессов, число которых больше трех благодаря микроблочному строению цепей сополимеров.

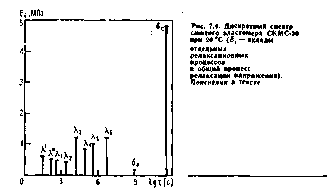
Рисунок 2.10 – Дискретный спектр

Для этого эластомера энергия активации U_0c = 143 кДж/моль, а коэффици­ент B_i=3,2*10^-4с. Столь малое значение В_i, меньшее, чем для γ- и δ-процессов, свидетельствует о том, что этот процесс является мелкомасштабным. Период колебаний атомов углерода в связях С—С, по данным ИКС, τ₀≈ 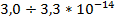с, что совпадает с значением Bi. А так как в формуле B_i имеет смысл периода колебания, то тем самым доказано, что кинетической единицей в δс-процессе является атом углерода в полимерной цепи.

По данным масс-спектрометрического термического анализа (МТА) для СКМС-30, энергия активации тер­модеструкции связей С—С на первой стадии 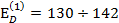кДж/моль, что близко к энергии активации δс-процесса релаксации. Данные МТА для ПММА: 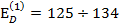кДж/моль, а энергия активации раз­рушения U₀=134 кДж/моль. Итак, можно сказать, что энергии активации трех процессов: химической релаксации, термиче­ской деструкции и процесса разрушения (при ϭ→0) совпа­дают.

Для эластомера СКМС-30, сшитого серой, возникает до­полнительный процесс химической релаксации δs (см. рисунок 2.9) с небольшим вкладом (см. рисунок 2.11). Коэффициент Bi = = 6,6*10^-14 с, а энергия активации Uδ_s = 126 кДж/моль. Суть этого процесса, со­стоит в непрерывной перестройке сетки путем разрыва и ре­комбинации

поперечных связей S—S (обменная реакция). По данным ИКС, волновое число для связей S—S равно 400 см-¹, что соответствует периоду колебаний атомов τ₀ = 8,3*10^-14 с.

К шестой группе релаксационных переходов, таким образом, относятся химические процессы релаксации.

Дата добавления: 2015-08-20