Химические осцилляторы

1. Математическая модель и производная второй вариации энтропии

2. Изменение избытка энтропии за счёт теплообмена с окружающей средой

3. Изменение избытка энтропии за счёт массообмена с окружающей средой

4. Простая необратимая реакция

4.1. Вывод выражения для избыточного производства энтропии

4.2. Анализ устойчивости режима в реакторе

4.3. Задача о тепловой устойчивости процесса

5. Автокаталитическая реакция

5.1. Вывод выражения для избыточного производства энтропии

5.2. Анализ устойчивости режима в реакторе

6. Простая реакционная схема

6.1. Вывод выражения для избыточного производства энтропии

6.2. Анализ устойчивости режима в реакторе с помощью критерия Сильвестра

7. Реакционные схемы Белоусова-Жабо­тинского и Бриггса-Раушера

7.1. Выражения для производной второй вариации энтропии

7.2. Анализ причин осцилляций

8. Осцилляторы в реакторах с рециклами

8.1. Математическое описание реактора с рециклом

8.2. Анализ влияния рецикла на устойчивость режима в реакторе

9. Классификация колебательных процессов в химии

1. Математическая модель и производная второй вариации энтропии

Рассмотрим ёмкостной проточный реактор смешения с охлаждением через рубашку, в котором могут происходить реакции типа

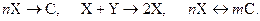
Математическая модель проточного реактора смешения имеет вид:

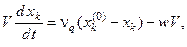
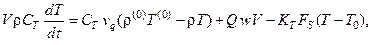
где 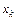– концентрация k -го компонента; 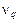– объёмный расход поступающего раствора; w - скорость химической реакции; Q - тепловой эффект реакции; 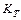– коэффициент теплопередачи; V - рабочий объём реактора; 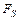– поверхность реактора; 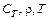– теплоёмкость, плотность и температура смеси в реакторе; 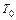– температура хладагента в рубашке; индекс (0)означает значение параметра на входе в реактор.

Поскольку реакции протекают в ёмкостном реакторе с мешалкой, в качестве необратимых процессов следует рассматривать только непосредственно химические превращения. Соотношение для производной второй вариации энтропии (5.7) при этом преобразуется к виду:

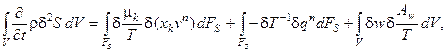(6.1)

где 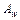– сродство химической реакции; 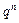– тепловой поток через единицу поверхности реактора; 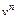– скорость движения реакционной смеси; 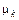– химический потенциал k -го компонента; индекс n означает проекцию вектора на нормаль к поверхности реактора F_S.

Первое и второе слагаемые в правой части выражения (6.1) характеризуют изменение избытка энтропии за счёт тепло- и массообмена системы с окружающей средой, т.е. за счёт наличия протока через реактор и теплообмена через поверхность реактора с хладагентом в рубашке; таким образом, эти слагаемые определяются только конструкционными особенностями реактора. Последнее слагаемое является избыточным производством энтропии; оно зависит от типа химических превращений, протекающих в реакторе.

Напомним, что вторая вариация энтропии является термодинамической функцией Ляпунова для систем, удалённых от равновесия, и согласно второму методу Ляпунова производная этой функции должна быть положительной, чтобы стационарное состояние системы было устойчивым. Однако даже при отсутствии возможности рассчитать величину в выражении (6.1) простой анализ знаков отдельных слагаемых позволяет сделать важные выводы о том, какие процессы дестабилизируют систему (описывающие их члены в выражении (6.1) будут всегда отрицательны), а какие, наоборот, – повышают её устойчивость (описывающие их члены – всегда положительны), и как необходимо изменить условия протекания процесса, чтобы ослабить влияние первых и усилить влияние вторых.

2. Изменение избытка энтропии за счёт теплообмена с окружающей средой

Получим выражение для изменения избытка энтропии проточного реактора с мешалкой за счёт обмена энергией с окружающей средой:

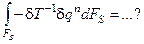
Вариация от величины, обратной температуре в реакторе, определяется согласно правилам дифференцирования:

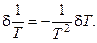
Тепловой поток из реактора в окружающую среду, отнесённый к единице поверхности реактора, определяется по формуле:

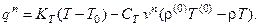
Первое слагаемое в правой части этого уравнения характеризует отвод тепла через поверхность реактора за счёт теплообмена с хладагентом в рубашке; второе слагаемое – изменение теплоты реакционной смеси за счёт наличия протока через реактор.

Допуская, что температура питательного раствора и температура хладагента в рубашке – величины постоянные, получим вариацию от теплового потока :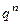

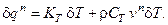
Подставим полученные выражения для вариаций в исходную формулу:

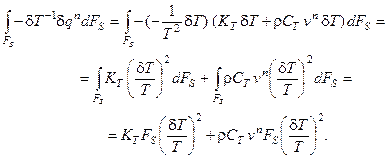
Учитывая, что

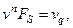
получим итоговое выражение для изменения избытка энтропии проточного реактора с мешалкой за счёт обмена энергией с окружающей средой:

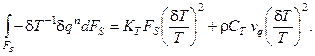(6.2)

Отметим, что выражение (6.2) определяется только типом реактора и не зависит от того, какие химические превращения в нём протекают, что позволяет его применять для любой реакционной схемы.

3. Изменение избытка энтропии за счёт массообмена с окружающей средой

Получим выражение для изменения избытка энтропии проточного реактора с мешалкой за счёт массообмена с окружающей средой (т.е. за счёт наличия протока через реактор):

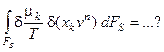
Рассмотрим сначала случай, когда во входящем и выходящем потоках имеется только один компонент Х, концентрация которого влияет на протекание химического процесса в реакторе. Химический потенциал данного компонента связан с его концентрацией х соотношением:

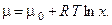
Следовательно, вариация от химического потенциала, отнесённого к температуре, будет определяться следующим образом:

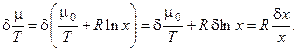
Отметим, что при рассмотрении массообмена системы с окружающей средой нас интересуют только вариации по концентрациям компонентов системы, поэтому первое слагаемое в полученном выражении приравнено нулю.

Подставим полученное выражение в исходную формулу:

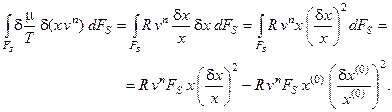
Учитывая, что

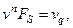
получим итоговое выражение для изменения избытка энтропии проточного реактора с мешалкой за счёт массообмена с окружающей средой (для одного компонента системы):

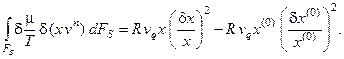(6.3)

В случае, если во входящем и выходящем потоках будет несколько компонентов, влияющих на протекание химического процесса в реакторе, выражение (6.3) преобразуется к виду:

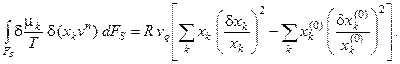(6.3а)

Отметим, что полученные выражения, как и формула (6.2), определяются только типом реактора и не зависят от того, какие химические превращения в нём протекают, что позволяет их применять для любой реакционной схемы.

4. Простая необратимая реакция

4.1. Вывод выражения для избыточного производства энтропии

Пусть в проточном реакторе с мешалкой протекает простая необратимая реакция типа

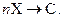
Скорость и химическое сродство такой реакции имеют вид:

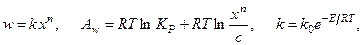
где k - константа скорости химической реакции; Е - энергия активации химической реакции; х - концентрация вещества Х; с - концентрация продукта реакции; 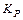– константа равновесия химической реакции.

Получим вариацию от термодинамического потока процесса (скорости реакции):

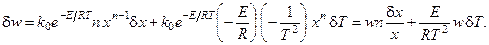
Получим вариацию от термодинамической движущей силы процесса (химического сродства, отнесённого к температуре реакционной смеси):

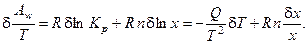
Поскольку в данной реакции концентрация конечного продукта не влияет на протекание процесса, вариация по ней не рассматривается.

Таким образом, избыточное производство энтропии процесса имеет вид:

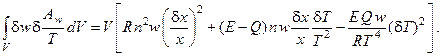(6.4)

Подставляя выражения (6.2), (6.3) и (6.4) в (6.1), получим в явном виде производную термодинамической функции Ляпунова (второй вариации энтропии) для проточного реактора с мешалкой, в котором протекает простая необратимая реакция:

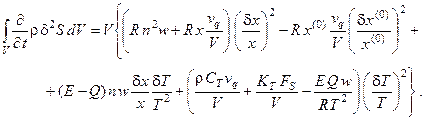(6.5)

Отметим, что производная второй вариации энтропии является квадратичной формой, и если эта форма положительно определена, то стационарное состояние системы устойчиво, если – отрицательно определена, то – неустойчиво; определить же знак квадратичной формы можно с помощью критерия Сильвестра.

4.2. Анализ устойчивости режима в реакторе

Проанализируем выражение (6.5). Члены, положительность которых очевидна, соответствуют процессам, стабилизирующим рассматриваемую систему:

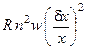· – наличие в системе прямой реакции;

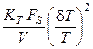· – наличие теплоотвода через стенку реактора;

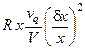· – наличие оттока реагентов из реактора;

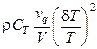· – наличие протока (повышает тепловую устойчивость системы).

Члены, отрицательность которых очевидна, соответствуют процессам, дестабилизирующим систему:

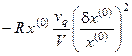· – наличие пульсаций 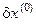во входном потоке;

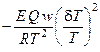· – выделение тепла в ходе химической реакции.

Таким образом, если в выражении (6.5) превалируют члены, связанные с тепловыделением в ходе химической реакции и пульсациями во входном потоке, то исследуемый режим неустойчив. Каким образом можно ликвидировать или хотя бы ослабить влияние этих эффектов на практике?

1. повысить интенсивность теплоотвода через стенку реактора (например, за счёт понижения температуры хладагента или увеличения его расхода), повышая, таким образом, тепловую устойчивость системы;

2. устранить (если это возможно) пульсации во входном потоке;

3. увеличить (если это возможно) рабочий объём аппарата, что приведёт к более эффективному гашению пульсаций во входном потоке.

4. Простая необратимая реакция

4.3. Задача о тепловой устойчивости процесса

Анализ устойчивости химического процесса в проточном реакторе с мешалкой свидетельствует о том, что наличие прямых реакций приводит к стабилизации концентрационного режима, т.е. рассматриваемый реакционный механизм не может вызвать появление концентрационных пульсаций в реакторе. Однако в такой системе может возникнуть тепловая неустойчивость при высоких тепловых эффектах химических реакций и недостаточном теплоотводе. Зависимость константы скорости химической реакции от температуры приведёт к тому, что при возникновении в системе пульсаций по температуре могут возникнуть и концентрационные пульсации, что не позволит гарантировать стабильность свойств получаемого продукта. Таким образом, задаче о тепловой устойчивости химического процесса в реакторе следует уделить особое внимание. Рассмотрим подход к её решению на примере простой необратимой реакции в проточном реакторе с мешалкой.

Пусть для рассматриваемой системы гарантирована стабильность концентраций всех компонентов, как в самом реакторе, так и во входном потоке, т.е.

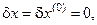
и допускаются только пульсации по температуре 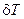. Выражение для производной термодинамической функции Ляпунова (второй вариации энтропии системы) (6.5) при этом преобразуется к виду:

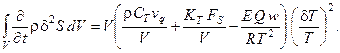
Видно, что производная термодинамической функции Ляпунова положительна при условии:

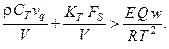
Отсюда можно получить зависимость для управляющего параметра химического процесса – времени пребывания в реакторе, при котором тепловая устойчивость системы будет гарантирована:

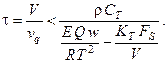
5. Автокаталитическая реакция

5.1. Вывод выражения для избыточного производства энтропии

Пусть в проточном реакторе с мешалкой протекает автокаталитическая реакция

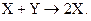
Скорость и химическое сродство такой реакции имеют вид:

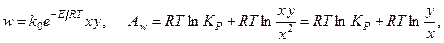
где х - концентрация вещества Х; y - концентрация вещества Y.

Получим вариацию от термодинамического потока процесса (скорости реакции):

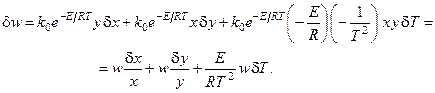
Получим вариацию от термодинамической движущей силы процесса (химического сродства, отнесённого к температуре реакционной смеси):

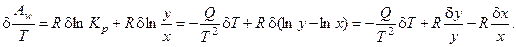
Таким образом, избыточное производство энтропии процесса имеет вид:

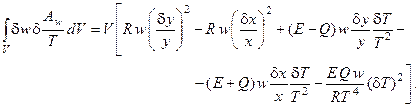(6.6)

Подставляя выражения (6.2), (6.3а) и (6.6) в (6.1), получим в явном виде производную термодинамической функции Ляпунова (второй вариации энтропии) для проточного реактора с мешалкой, в котором протекает автокаталитическая реакция:

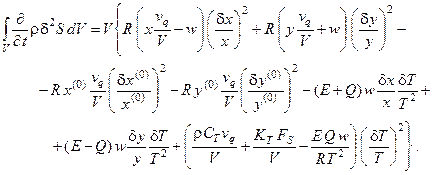(6.7)

Напомним, что если выражение (6.7), являющееся квадратичной формой, положительно определено, то стационарное состояние системы устойчиво, если – отрицательно, то состояние – неустойчиво (согласно второму методу Ляпунова). Для определения знака квадратичной формы используется критерий Сильвестра.

5.2. Анализ устойчивости режима в реакторе

При анализе выражения (6.7) остановимся подробно только на тех эффектах, которые не рассматривались при анализе устойчивости химического процесса с простой необратимой реакцией. Так, член

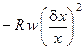
характеризует непосредственно автокаталитический химический процесс. Очевидно, что он имеет отрицательный знак, что усиливает дестабилизацию системы.

Слагаемое

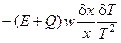
соответствует термокинетическому эффекту: если увеличение температуры (которое может произойти вследствие интенсивного тепловыделения в процессе реакции) способствует ускорению реакции, то в системе будет происходить накопление вещества X, т.е.

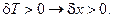
Следовательно, данное слагаемое будет иметь отрицательный знак, что также усиливает дестабилизацию системы.

Таким образом, наличие в системе автокаталитических химических реакций понижает устойчивость системы, дестабилизирует её как за счёт самого реакционного механизма, так и за счёт термокинетических связей. Если вклад этих эффектов начинает преобладать, то исследуемый режим становится неустойчивым и в системе возможно возникновение диссипативных структур.

6. Простая реакционная схема

6.1. Вывод выражения для избыточного производства энтропии

Пусть в периодическом реакторе с мешалкой осуществляется двухстадийная химическая реакция:

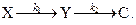
Скорость и химическое сродство для каждой стадии процесса определяются по формулам:

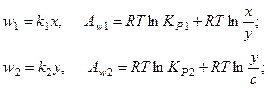
где х - концентрация вещества Х; y - концентрация вещества Y; с - концентрация продукта реакции; 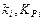- константа скорости и константа равновесия i -й стадии (i = 1,2).

Рассмотрим случай, когда тепловая устойчивость для данной системы гарантирована, т.е. 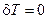, и возможны только колебания концентраций реагентов 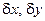; вариация по концентрации конечного продукта, как не влияющего на протекание процесса, также не будет учитываться.

Получим вариацию от термодинамического потока для каждой стадии процесса:

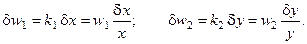
Получим вариацию от термодинамической движущей силы (химического сродства, отнесённого к температуре реакционной смеси) для каждой стадии процесса:

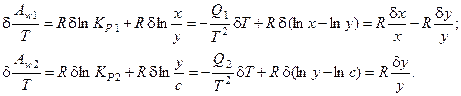
Таким образом, избыточное производство энтропии процесса имеет вид:

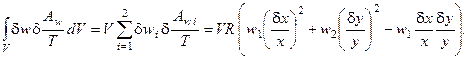(6.8)

Поскольку мы рассматриваем реактор периодического действия, в котором гарантирована тепловая устойчивость процесса, изменение избытка энтропии за счёт теплообмена (6.2) и массообмена (6.3а) системы с окружающей средой будет равно нулю и, следовательно, выражение (6.8) является производной термодинамической функции Ляпунова (второй вариации энтропии) для рассматриваемого процесса.

6.2. Анализ устойчивости режима в реакторе с помощью критерия Сильвестра

Согласно второму методу Ляпунова знак производной второй вариации энтропии определяет устойчивость стационарных состояний систем, удалённых от равновесия: если эта величина положительна, то стационарное состояние системы устойчиво, если – отрицательна, то – неустойчиво. В то же время производная второй вариации энтропии системы является квадратичной формой, что позволяет исследовать её знак с помощью критерия Сильвестра.

Критерий Сильвестра. Для того, чтобы квадратичная форма

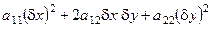
была положительно определена, необходимо и достаточно, чтобы все главные диагональные миноры матрицы квадратичной формы были строго положительны:

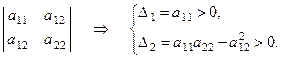
Если же знаки главных диагональных миноров матрицы квадратичной формы чередуются, причём первый из них отрицателен

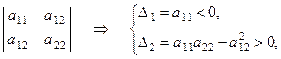
то данная квадратичная форма является отрицательно определённой.

С помощью критерия Сильвестра определим, при каких условиях квадратичная форма (6.8) является положительно определённой. Составим для неё матрицу квадратичной формы и определим главные диагональные миноры этой матрицы:

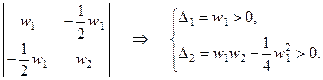
Первое условие выполняется автоматически. Из второго условия получаем:

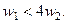
Таким образом, гарантировать положительный знак производной термодинамической функции Ляпунова для рассматриваемого реакционного процесса (т.е. его устойчивость) можно только при выполнении данного соотношения между скоростями его стадий.

7. Реакционные схемы Белоусова-Жабо­тинского и Бриггса-Раушера

7.1. Выражения для производной второй вариации энтропии

Реакционная схема Белоусова-Жабо­тинского имеет вид:

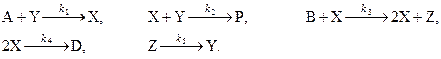
Реакционная схема Бриггса-Раушера имеет вид:

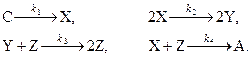
Приведём производную термодинамической функции Ляпунова (второй вариации энтропии) для реактора периодического действия с мешалкой, в котором осуществляются эти реакции (учитываются вариации по концентрациям реагентов X, Y, Z и по температуре):

· для реакционной схемы Белоусова-Жабо­тинского

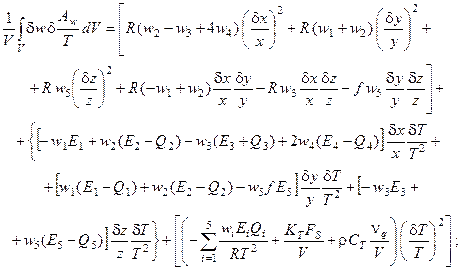(6.9)

· для реакционной схемы Бриггса-Раушера

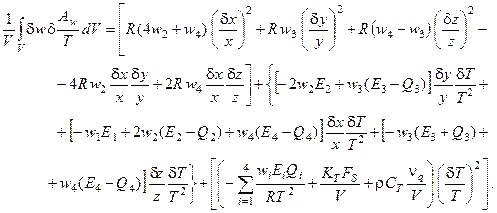(6.10)

7.2. Анализ причин осцилляций

Реакционные схемы Белоусова-Жаботинского и Бриггса-Раушера являются примером химических осцилляторов, способных вызвать колебания концентраций реагентов, образование сложных упорядоченных структур (диссипативных структур). Анализ производных термодинамической функции Ляпунова (второй вариации энтропии) (6.9) и (6.10) позволяет выявить причины этих явлений самоорганизации.

Прежде всего, это наличие в реакционных схемах Белоусова-Жаботинского и Бриггса-Раушера автокаталитических реакций (в обоих случаях это реакция № 3), приводящее к появлению отрицательных слагаемых в выражениях (6.9) и (6.10), которые связаны как с самим реакционным механизмом автокаталитического процесса, так и с термокинетическим эффектом. Более подробно дестабилизирующее влияние автокаталитической реакции было рассмотрено ранее на простом примере.

Рассмотрение сложных реакционных схем позволяет подытожить результаты термодинамического анализа (анализа производной термодинамической функции Ляпунова), с помощью которого был выявлен класс химических осцилляторов и определены причины возникновения колебательных явлений в системах с химическими реакциями:

1) наличие источников поступления вещества и энергии (открытость системы);

2) удалённость системы от равновесия, которая обусловливает её нелинейность;

3) наличие обратных связей в виде автокаталитической петли;

4) наличие термокинетических связей;

5) интенсивное выделение тепла в ходе химических реакций при недостаточном теплоотводе.

8. Осцилляторы в реакторах с рециклами

8.1. Математическое описание реактора с рециклом

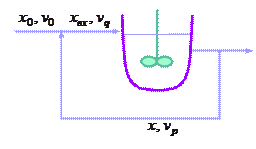Рассмотрим проточный химический реактор смешения с рециклом (см. рисунок), в котором протекает автокаталитическая реакция типа

Объёмный расход потока, протекающего через реактор, определяется как сумма объёмных расходов питающего раствора и рецикла:

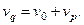
Материальный баланс по компоненту Х для точки смешения потоков имеет вид:

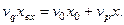
Отсюда имеем концентрацию компонента Х на входе в реактор:

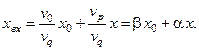
Здесь 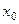– концентрация питающего раствора; х – концентрация компонента Х в реакторе (а, следовательно, и в рецикле), b – доля питающего раствора; a – доля рецикла.

Вывод производной термодинамической функции Ляпунова (второй вариации энтропии) (6.7) для проточного реактора с мешалкой, в котором протекает автокаталитическая реакция, был подробно описан ранее. При изучении влияния рецикла на устойчивость системы целесообразно рассмотреть случай, когда гарантирована тепловая устойчивость, т.е. 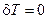, и возможны только вариации концентрации реагента Х. Перепишем соотношение (6.7), сделав в нём соответствующие упрощения и коррекцию обозначений:

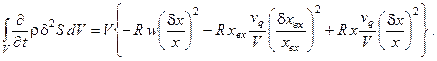(6.11)

Здесь w – скорость химической реакции, V – объём реактора.

8.2. Анализ влияния рецикла на устойчивость режима в реакторе

Чтобы понять, как влияет наличие рецикла на устойчивость режима в реакторе, рассмотрим и сравним два крайних случая.

1. Наличие в системе большого рецикла, т.е. если расход питающего раствора пренебрежимо мал по сравнению с расходом рецикла:

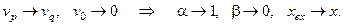
Соотношение (6.11) при этом преобразуется к виду:

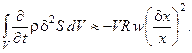
Анализ полученного выражения говорит о том, что на устойчивость режима в реакторе с большим рециклом оказывает влияние только механизм реакционной схемы; поэтому если он будет причиной возникновения в системе концентрационных колебаний, система не сможет их сгладить. В то же время наличие существенных пульсаций концентраций реагентов в питающем потоке не оказывает на систему заметного воздействия, поскольку большой рецикл гасит их, оставляя только влияние собственно реакционного механизма.

2. Отсутствие рецикла, т.е. если расход рецикла пренебрежимо мал по сравнению с расходом питающего раствора:

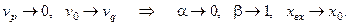
Соотношение (6.11) при этом преобразуется к виду:

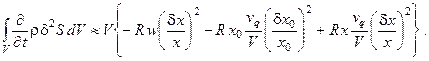
Видно, что в системе без рецикла неустойчивость может возникнуть как за счёт реакционного механизма, так и за счёт пульсаций в питающем потоке. Однако стабилизирующая роль протока реагентов через реактор здесь более существенна, чем в случае большого рецикла; поэтому если возникают концентрационные колебания за счёт механизма реакций (при условии отсутствия пульсаций в питающем потоке), система без рецикла пытается сгладить их.

Таким образом, рецикл в системе играет роль обратной связи, хотя действует не так явно, как автокаталитическая обратная связь.

9. Классификация колебательных процессов в химии

Подводя итог данному разделу, перечислим типы осцилляторов в химии и химической технологии, которые позволил выявить термодинамический анализ (анализ производной термодинамической функции Ляпунова):

· химические,

· термокинетические,

· газофазные,

· осцилляторы в гетерогенном катализе,

· осцилляторы при кристаллизации,

· осцилляторы в реакторах с рециклом,

· осцилляторы, где пульсации возникают из-за гидродинамической неустойчивости (аппараты с псевдоожиженным и фонтанирующим слоями),

· осцилляторы в совмещённых процессах, объединённых наличием обратной связи.

Выявлены причины возникновения диссипативных структур и автоколебательных режимов в химии и химической технологии:

1) наличие источников поступления вещества и энергии (открытость системы);

2) удалённость системы от равновесия, которая обусловливает её нелинейность (наличие нелинейных связей между потоками и движущими силами);

3) наличие автокаталитических обратных связей;

4) наличие термокинетических связей;

5) наличие обратных связей в виде рецикла;

6) интенсивное тепловыделение при недостаточном теплоотводе;

7) конвекция;

8) гетерогенность;

9) наличие вещества с высокой способностью к пересыщению (для процесса кристаллизации);

10) наличие обратной связи в совмещённых процессах.

Дата добавления: 2015-08-20