Свойства

Ø Если площадь основания конечна, то объём конуса также конечен и равен трети произведения высоты на площадь основания.

Ø где S — площадь основания, H — высота. Таким образом, все конусы, опирающиеся на данное основание (конечной площади) и имеющие вершину, находящуюся на данной плоскости, параллельной основанию, имеют равный объём, поскольку их высоты равны.

Ø Центр тяжести любого конуса с конечным объёмом лежит на четверти высоты от основания.

Ø Телесный угол при вершине прямого кругового конуса равен

где α — угол раствора конуса.

Ø Площадь боковой поверхности такого конуса равна

Полная площадь поверхности (т. е. сумма площадей боковой поверхности и основания)

где R — радиус основания, l — длина образующей.

Ø Объём кругового конуса равен

Ø Для усечённого конуса (не обязательно прямого и кругового) объём равен:

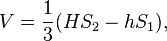
где S₁ и S₂ — площади соответственно верхнего (ближнего к вершине) и нижнего оснований, h и H — расстояния от плоскости соответственно верхнего и нижнего основания до вершины.

Ø Пересечение плоскости с прямым круговым конусом является одним из конических сечений (в невырожденных случаях — эллипсом, параболой или гиперболой, в зависимости от положения секущей плоскости).

Дата добавления: 2015-08-18