Итак, статистики для номинальных и порядковых данных.

Вопрос на засыпку: чем отличаются порядковые данные от номинальных?

Ответили, идем дальше.

Статистики же в нашем случае – это числовые показатели. Кто-то, наверное, запомнил из лекции слово хи-квадрат. Значение хи-квадрат – это статистика. Значения коэффициентов, измеряющих силу связи между переменными – это статистики.

Сначала, зачем все это надо.

Простейший анализ таблиц сопряженности признаков выполняется через рассмотрение распределения частот и процентных значений (т.е. долей) по переменным.

Таблица сопряженности - таблица, в которой по строкам располагаются значения одной переменной, а по столбцам – значения другой переменной.

Например, Таб.1 (в %):

Тип жилья	Район города
Западный	Восточный	Северный	Южный	Всего
Собственное жилье	63,1	29,2	48,3	66,6
Сдающееся в наем	30,2	58,8		24,4
Организации	6,6		11,6	8,9
Всего	100 (225)	100 (250)	100 (300)	99,9 (225)	100 (1000)

По строкам располагаются значения переменной «тип жилья», по столбцам располагаются значения переменной «район города».

Мы можем нарисовать столбиковые или круговые диаграммы для быстрого анализа частотного/процентного распределения значений.

В случае, если у нас только два значения двух переменных, то особой надобности в статистических расчетах нет. Например, если наша таблица выглядит так:

Таб.2

Тип жилья	Район города
Западный	Восточный
Собственное жилье	63,1	36,9

то особой надобности в расчетах нет.

Но если таблица выглядит как Таб.1., т.е. у нас несколько категорий у каждой переменной (переменная «тип жилья» имеет несколько категорий: «собственное жилье», «жилье, сдаваемое в аренду», «помещения, занимаемые организациями»), то статистический анализ обязателен.

Что здесь нужно учитывать. При статистическом анализе формулируются две гипотезы: нулевая гипотеза об отсутствии связи между переменными, и альтернативная гипотеза о наличии связи между переменными. Проверяется всегда нулевая гипотеза, т.е. мы ориентируемся на проверку гипотезы об отсутствии связи между переменными.

Речь идет о тестировании (проверке) статистической значимости связей между переменными. Как правило, для тестирования этой значимости необходимо выполнение некоторых требований, основным из которых является соответствие данных нормальному распределению, т.е. вспоминаем прошлую лекцию: 99,73% случаев должно лежать в пределах трех стандартных отклонений. В нашем случае это означает, что... нет, не будем об этом просто потому, что хи-квадрат - это непараметрическая статистика, что означает, что мы можем проигнорировать это требование. Другое дело, что данные нужно собирать по случайной выборке (или разновидностям случайной выборки), это ключевое условие. Не смогли собрать данные по случайной выборке - не можем обобщить результаты анализа на нашу генеральную совокупность.

Далее, наличие статистической значимости не является доказательством реальной значимости. Связь между импортом апельсинов и ростом раковых заболеваний в стране может быть статистически значимой, но по факту такое предположение является чепухой. Следовательно, многое зависит от нашей выбранной модели анализа, или, другими словами, от того, как мы объясняем то или иное явление.

Для анализа связей между номинальными переменными (т.е. характеристиками изучаемых явлений, которые нельзя упорядочить «естественным» путем, как, например, нельзя упорядочить в терминах «больше-меньше» переменную «пол» - ведь что значит, «свойство «мужчина» больше свойства «женщина»?) в таблицах сопряженности используются меры связи, включающие статистики хи-квадрат, коэффициенты Фи, протяженности Пирсона, V Крамера, а также, основанные на расчетах пропорционального уменьшения ошибки (способ, отличающийся от расчетов статистик на основе хи-квадрат) коэффициенты лямбда и тау Гудмена-Краскала.

Теперь бонус для студентов. Мы будем заниматься расчетом только статистики хи-квадрат и коэффициентов на ее основе, но для тех, кто хочет хорошую или даже отличную оценку нужно не просто научиться рассчитывать эти статистики, но членораздельно объяснять, что же они все таки сделали, что все это означает. С этим у многих студентов трудности, поэтому могу рекомендовать только одно: читать внимательнее. Анализом порядковых данных, пожалуй, мы тоже заниматься не будем.

Расчеты будут делаться в Екселе, поэтому R устанавливать не нужно.

Итак, Таб.3.

	Должность
Пол	Специалисты	Администраторы	Клерки	Продажники	Сектор услуг	Производство	Итого
Мужчины
Женщины
Пол не имеет значения
Итого

Расшифровка: мы исследуем гипотетическую связь между требованиями работодателя к полу соискателя должности и самой должностью. Можем ли мы сказать, к примеру, что на определенные категории должностей требуются люди определенного пола?

Анализ осуществляется через рассмотрение объявлений работодателей, размещенных в СМИ. В объявлении указаны требования к полу, либо не указаны. Следовательно, по строкам таблицы размещены категории переменной «требования к полу», в колонках таблицы размещены указанные в объявлении категорий должностей. Есть ли связь между требованиями работодателя к полу и должностью, на которую работодатели пытаются найти сотрудника?

Решение:

Статистика хи-квадрат основывается на сравнении ожидаемого числа случаев в каждой ячейке таблицы с реальными наблюдениями.

Допустим, требования работодателя к полу сотрудника никак не связаны с предлагаемой должностью (женщины могут работать шпалоукладчицами, а мужчины могут работать косметологами безо всяких предубеждений). Тогда распределение женщин и мужчин в строках таблицы будет пропорционально числу объявлений работодателя, т.е. ожидаемые (теоретические) частоты – это частоты, показывающие распределение значений так, как если бы они не зависели от значений других переменных.

Сначала рассчитываем ожидаемые значения в ячейках таблицы (результаты округляем).

Формула:

Ожидаемое (i,j) = [сумма по строке(i) * сумма по столбцу(j)] / N, где N - общая сумма случаев в таблице.

	Должность
Пол	Специалисты	Администраторы	Клерки	Продажники	Сектор услуг	Производство	Итого
Мужчины	931/ 823
Женщины	256/312
Пол не имеет значения	1544/902
Итого

Первая колонка:

1940*2731/6441=823

737*2731/6441=312

3764*2731/6441=902

Вторая колонка:

1940*990/6441=298

737*990/6441=113

3764*990/6441=578

и т.д.

После того, как вычислили все ожидаемые частоты в таблице, производим расчет статистики хи-квадрат.

Хи-квадрат =∑[наблюдаемые(i, j) - ожидаемые(i, j)]²/ожидаемые(i, j)

i и j = 1 для k и r соответственно, где k – это число столбцов, а r – число строк.

Проще говоря, мы в каждой ячейке таблицы отнимаем ожидаемые частоты от наблюдаемых, возводим результат в квадрат и делим на ожидаемые частоты из этой же ячейки. Например, ячейка мужчины-специалисты (931/ 823):

(931/823)²/823. Это нужно сделать в каждой ячейке, а результаты потом сложить (если угодно, сначала по столбцам, потом между собой). Получится итоговое значение хи-квадрат.

Теперь, как облегчить себе задачу. В экселе есть специальная функция хи-квадрат, но мы сделаем наглядно.

Копируем итоговые значения таблицы (проще скопировать всю таблицу и удалить все значения, кроме итоговых):

Теперь выделим прямоугольный диапазон с пустыми ячейками внутри будущей таблицы ожидаемых частот. Нажимаем знак равенства и вводим формулу: выделяем строку итогов, жмем * (знак умножения), затем выделяем столбец итогов, нажимаем / (знак деления), потом кликаем по ячейке с общим итогом в таблице и жмем сочетание клавиш Shift+Control+Enter для того, чтобы вставились все результаты расчета, а не один.

Получившиеся результаты можно округлить: нужно выделить диапазон с получившимися значениями, правой кнопкой мыши вызвать контекстное меню - Формат ячеек-Числовой-Число десятичных знаков - 2.

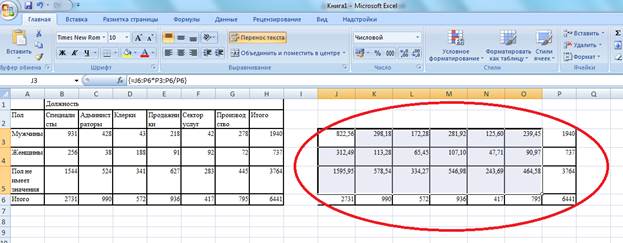
Мы выделяем диапазон значений в новой табличке, равный диапазонам значений в первых двух таблицах, вводим формулу (знак =, затем выделяем диапазон наблюдаемых значений (первая таблица), умножаем (знак *) на ожидаемые значения (все это заключается в скобки) и делим на ожидаемые значения. Как и в прошлом случае, чтобы в новую табличку вставились все новые значения, жмем клавиши Shift+Control+Enter. Результаты можно округлить указанным выше способом. Получившиеся значения складываем. Итоговое значение статистики хи-квадрат = 607,2.

Что это значит? Нам нужно оценить результат при помощи таблиц распределения статистики хи-квадрат. Таблицы легко находятся в интернете (главное, не перепутать с другими статистическими таблицами), но вот образец из лекции:

Количество степеней свободы — это количество значений в итоговом вычислении статистики, способных варьироваться.

Если немного подробней про число наблюдений, способных варьироваться, то можно объяснить так:

у нас есть четыре элемента (a, b, c, d), в сумме они дают m. Мы можем выбрать любые три из них (т.е. они варьируются), но последний элемент обязательно нужен для того, чтобы сумма стала m, т.е. в этом отношении выбор уже не свободен.

Или же это число независимых элементов информации, на которых базируется оценка. В нашем случае это количество равно N-1, где N - число клеток в таблице. В таблице 2Х2 число степеней свободы = 1, т.к. (r–1)(c–1) = (2-1)Х(2-1)=1. Наша таблица имеет вид 6Х3 (считаются строки и столбцы, не содержащие итоговых значений), следовательно, число степеней свободы = (6-1)(3-1)= 5*2 =10.

Уровень значимости оценивается через p-value, или вероятность, с которой нулевая гипотеза об отсутствии связи окажется верной. Традиционно выбирается уровень значимости в 5%. (т.е. 0,05). Все, что ниже этого уровня, обладает низкой значимостью. 5% означает, что с 95% вероятностью наши результаты не случайны.

Итак, десять степеней свободы при уровне значимости в 0,05. Смотрим значение в таблице на пересечении степеней свободы и уровня значимости:

Таблица показывает значение в 18,3. Это меньше, чем 607,2. Следовательно, мы можем отбросить нулевую гипотезу об отсутствии связи между нашими переменными («пол» и «должность») и можем принять альтернативную гипотезу, что связь есть. Но мы ничего не можем сказать о том, насколько сильна эта связь. Еще раз: да, значение 607,2 больше, чем 18, 3, но о силе связи это ничего не говорит. Главное, что оно просто больше. Сила связи в статистике обычно определяется через коэффициент, варьирующийся от -1 до 1. Это означает, что при -1 наблюдается отрицательная связь между переменными (чем выше значение одной переменной, тем ниже значение другой и наоборот), при значении = 0 связь отсутствует, при значении =1 наблюдается положительная связь между значениями переменной (чем выше значение одной переменной, тем выше значение другой переменной, или же чем ниже значение одной переменной, тем ниже значение другой переменной). Но т.к. статистика хи-квадрат не позволяет определить направление связи, то в нашем случае коэффициенты будут варьироваться от 0 до 1, где 0 – полное отсутствие связи, а 1 – наличие сильной связи.

Что за коэффициенты?

Коэффициент Фи:

Т.е. статистику хи-квадрат (например, наши 607,2) делим на объем выборки (общее число случаев в таблице, например, наши 6441), а затем вычисляем корень кв. из этого числа.

Коэффициент протяженности Пирсона:

Хи-квадрат делим на сумму хи-квадрат и общего числа выборки, из числа извлекаем кв.корень.

Коэффициент V Крамера:

Где min – r или k, в зависимости от того, что меньше.

Вычисляем коэффициент фи, возводим его в квадрат, делим на число столбцов или строк, в зависимости от того, что меньше, из получившегося числа извлекаем кв.корень.

Все эти статистики равны 0, если две переменные статистически независимы. Их преимуществом является то, что их значения варьируются от 0 до 1, также, они остаются относительно стабильными, если большие таблицы трансформируются в малые (путем объединения значений). Также, они независимы от увеличения или уменьшения значений в клетках таблицы при сохранении пропорций (в отличие от статистики хи-квадрат). Изменение порядка в таблице не влияют на их значение.

Недостатки коэффициентов:

Фи-коэффициент может рассчитываться только для таблиц 2Х2. В больших таблицах значение коэффициента может превышать единицу.

Коэффициент протяженности Пирсона, наоборот, вне зависимости от силы связи между двумя переменными, никогда не достигает единицы. Для таблиц 2Х2 его значение максимум равно 0,707, оно увеличивается для таблиц большего размера, но никогда не достигает 1. Также, коэффициент протяженности обладает еще одним недостатком: его максимум зависит от числа клеток в таблице, что делает затруднительным сравнение таблиц различного размера.

Только V Крамера остается в диапазоне 0-1 и может достигать единицы в таблицах, где число строк не равно числу столбцов.

Таким образом, лучше рассчитывать коэффициент V Крамера.

Еще одно условие:

Хи-квадрат рассчитывается, если значение в ячейках не меньше 5, а общее число наблюдений не менее 20. Если это условие не выполняется, используется точный тест Фишера (его мы рассчитывать не будем).

Дата добавления: 2015-08-18