Laws of thermal radiation

Energy quantity emitted by a unit surface per unit time is called body radiation ability

, W/m².

Radiation ability Е corresponds to heat flux density q i.e. q = E.

Intensity of radiation is a quantity of energy emitted by the body in the range of wave-length from l to l+ dl related to considered wave-length dl

; W/m³.

Plank's law. On the basis of fundamental scientific researches in the field of thermal radiation M. Plank discovered dependence of blackbody radiation intensity on wave-length l and absolute temperature Т in 1900. This dependence is now referred to as Plank’s law and is written down as follows:

,

where е – natural logarithmic base;

l –length of emitted wave, m;

Т –temperature of emitting body, K;

c ₁, с ₂ –constants; с ₁=3,74∙10^-16 W·m², с ₂=1,44∙10^-2 m·K.

Plank constants allow to establish radiation intensity for any wave-length or spectral intensity depending on wave-length.

Two conclusions can be made on the basis of Plank’s law.

First conclusion: all bodies with temperature exceeding absolute zero emit energy into surroundings from their surface.

Second conclusion: the higher value of body temperature is the more energy is emitted to surroundings

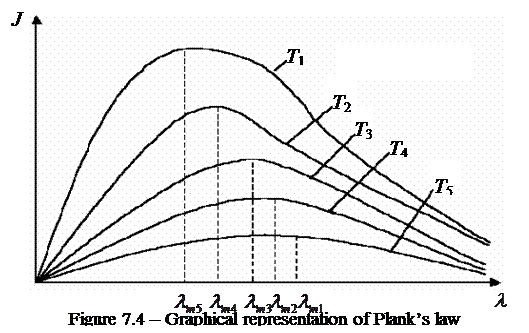
Graphical representation of Plank’s law is given on figure 7.4.

It follows from figure 7.4 that:

– with all the temperatures radiation intensity equals zero J ₀=0 if l=0 or l=∞;

– with temperature rise radiation intensity increases;

– maximums of radiation intensity curves are displaced in the direction of shorter waves on temperature increase

l_m5<l_m4< l _m3<l_m2<l_m1.

Rayleigh-Jeans law. Plank’s law has two bound cases. One of them occurs when

or .

In this case transformation based on expansion of into series is possible

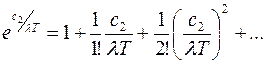
If l T >> с ₂ then we can confine ourselves to two first summands

Where from we get expression for Rayleigh -Jeans law

With high values of l Т which corresponds to curves right part, we get that radiation intensity is directly proportional to temperature and is reverse proportional to wave-length in fourth degree.

Law of displacement or Wien’s law. Second bound case corresponds to low values of product l Т. If T is very small then exponent index in Plank’s equation tends to ∞ and 1 can be neglected.

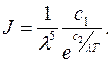
Wien ’s law represents radiation intensity as a function of temperature and wave-length

Taking derivative of radiation intensity in respect to wave-length and equating it to zero we get wave-length that corresponds to maximal radiation intensity at given temperature.

Relation between temperature Т and wave-length l_m corresponding to maximal radiation intensity is established by Wien’s law

m·K.

Using this law temperature of emitting body can be determined if wave-length corresponding to maximal radiation intensity is known. For example in the Sun’s spectrum maximum of radiation is carried by wave-length l_m=0,5mcm. Therefore temperature of the Sun’s emitting surface is about

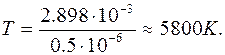
Stefan-Boltzmann law. Using Plank’s law energy emitted at a certain wave-length can be determined. Stefan-Boltzmann law allows to determine quantity of energy emitted by blackbody in the range of wave-length from l=0 to l=∞ at given temperature.

Total quantity of heat emitted at all the wave-lengths is called body radiation ability or body radiation density Е ₀, W/m²

,

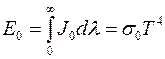where s₀ is called Stefan-Bolzmann constant and equals

, W/(m²·K⁴).

Since value of s ₀ is small and that of absolute temperature in the fourth degree is very high another expression for Stefan-Boltzmann law is used for practical calculations.

where с ₀ –coefficient of blackbody radiation:

W/(m²·K⁴).

Stefan-Boltzmann law holds true for blackbodies only.

Experiments done by Stefan and other researchers allowed to discover that this law can be applied not to blackbodies only but also to real bodies. In this case it must be written down in the form of following expression .

Radiation coefficient с is always lower than с ₀. It is determined by body nature, state of its surface and temperature. If spectral intensity of diffusive emitting body is the same fraction of blackbody intensity for all the wave-length at the same temperature then this body is termed as grey.

Comparing radiation ability of a grey body with that of blackbody we get another characteristic that is called integral or mean emissivity of a body.

The value of integral emissivity varies in the range 0< e <1.

Particular features of a grey body are:

– continuous spectrum in the whole range of wave-length;

– it is able to absorb not all the energy;

– integral emissivity has one and the same value for all the wave-length.

Heat exchange between two bodies according to Stefan-Boltzmann law. Let us consider two blackbodies located one near the other (figure7.5), so that no energy is lost through the gap.

First body emits energy in a quantity proportional to temperature Т ₁.

.

Another body emits energy proportional to temperature Т ₂.

.

Resultant heat flux is

.

The quantity of transferred heat is determined as

.

Kirchhoff’s law. This law establishes dependence between absorptive and reflective body properties.

First part: the more is absorptivity the more is emmissivity.

Second part: the body being hot is able to emit the same wave-length as it is able to absorb when the radiant energy falls onto it.

Let us consider two parallel planes with such a small gap between them that all the energy emitted by one surface falls onto the other. Both of the planes (figure 7.6) are in the state of thermodynamic equilibrium, i.e. they have the same temperatures. One of the surfaces is absolutely black and another is grey. Quantity of energy emitted by unit surface of blackbody per unit time is Е ₀. As closed system that consists of two infinite parallel planes is considered all this energy falls onto grey surface which absorbs energy in a quantity А ₁ Е ₀. Since the considered system is equilibrium grey surface temperature must remain unchanged according to second law of thermodynamics. Therefore grey surface emits as much energy as it absorbs А ₁ Е ₀= Е ₁.

Grey surface characterized by absorptivity A₁ can be replaced by any other grey surface with absorptivity A₂, A₃ etc. Derived relation can be presented as follows.

.

This relationship is called Kirchhoff’s law. Its essence can be presented as follows: ratio of body emissivity to absorptivity is the same for all the bodies having the same temperature and equals blackbody emissivity taken at the same temperature.

Comparing expressions Е=eЕ ₀ and Е=АЕ ₀ it can be noticed that grey body emissivity is equal to its absorptivity

e≡А,

i.e. the more is intensity of energy absorption by the body the more energy it can emit with other conditions being equal.

Emissivity – is ratio of energy emitted by given body to energy emitted by blackbody at the same temperature:

e =1 –blackbody; e =0 –absolutely white body.

For most bodies used in techniques emissivity equals e ~ 0,8.

Numerically emissivity is equal to absorptivity but their physical essence is different: coefficient А –characterizes body absorptive properties, e – emissitive properties.

Kirchhoff’s law can be also applied for studying monochromatic emission. In this case it is formulated like that: ratio of emissitive property for a certain wave-length to corresponding absorptive property is one and the same for all the bodies..

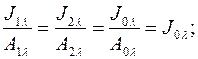
Square of distances law. It establishes dependence of heat flux density on distance from emitting body.

Let us consider a flux of radiant energy emitted by a small element or a point-like source in the range of a certain space angle. If the medium in which the energy moves is transparent then total power of radiant flux expressed in W remains unchanged at any distance from the cone vertex.

But density of radiant heat flux (its power related to flux unit surface W/m²) cannot remain unchanged because cone cross-section rises with distance from cone vertex increase.

Since the cone radius increases proportional to distance of considered plane to cone vertex and plane area is proportional to square of its radius density of radiant heat flux is reverse proportional to square of this distance (figure 7.7).

It can be got from triangles similarity

,

where from .

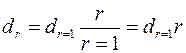Heat flux and ,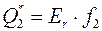

where

and .

As heat power is not changed with distance from the source increase

Then .

Or .

Дата добавления: 2015-08-17