Т-триггер асинхронный

Асинхронный Т-триггер не имеет входа синхронизации С.

Триггер синхронный - Синхронный Т-триггер ^[17][18], при единице на входе Т, по каждому такту на входе С изменяет своё логическое состояние на противоположное, и не изменяет выходное состояние при нуле на входе T. Т-триггер может строиться на JK-триггере, на двухступенчатом (Master-Slave, MS) D-триггере и на двух одноступенчатых D-триггерах и инверторе. Как можно видеть в таблице истинности JK-триггера, он переходит в инверсное состояние каждый раз при одновременной подаче на входы J и K логической 1. Это свойство позволяет создать на базе JK-триггера Т-триггер, объединяя входы J и К. Наличие в двухступенчатом (Master-Slave, MS) D-триггере динамического входа С позволяет получить на его основе T-триггер. При этом инверсный выход Q соединяется со входом D, а на вход С подаются счётные импульсы. В результате триггер при каждом счётном импульсе запоминает значение , то есть будет переключаться в противоположное состояние.

Т-триггер часто применяют для понижения частоты в 2 раза, при этом на Т вход подают единицу, а на С — сигнал с частотой, которая будет поделена на 2

21. Рассказать о видах позиционной системы счисления. Дать определение основания позиционной системы счисления. Привести развернутую форму записи числа, выраженного в позиционной системе счисления.

озиционная систе́ма счисле́ния (позиционная нумерация) — система счисления, в которой значение каждого числового знака (цифры) в записи числа зависит от его позиции (разряда).

Позиционная система счисления определяется целым числом b > 1, называемым основанием системы счисления. Система счисления с основанием b также называется b -ричной (в частности, двоичной, троичной, десятичной и т. п.).

Целое число x в b -ричной системе счисления представляется в виде конечной линейной комбинации степеней числа b:^[1]

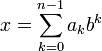, где 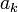— это целые числа, называемые цифрами, удовлетворяющие неравенству

Каждая степень 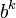в такой записи называется разрядом (позицией), старшинство разрядов и соответствующих им цифр определяется значением показателя степени 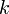. Обычно для ненулевого числа 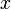требуют, чтобы старшая цифра 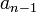в b -ричном представлении 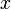была также ненулевой.

Если не возникает разночтений (например, когда все цифры представляются в виде уникальных письменных знаков), число 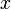записывают в виде последовательности его b -ричных цифр, перечисляемых по убыванию старшинства разрядов слева направо:^[1]

Построение такой записи числа называют позиционным кодированием числа, а саму запись — позиционным кодом числа.

Например, число сто три представляется в десятичной системе счисления в виде:

Во избежание путаницы при одновременной работе с несколькими системами счисления основание указывается в качестве нижнего индекса:

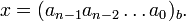
С помощью n позиций в b -ричной системе счисления можно записать целые числа от 0 до bⁿ − 1, то есть, всего bⁿ различных чисел.

22. Раскрыть принцип работы синхронного D-триггера. Изобразить условное графическое обозначение. Привести таблицу состояний. Сформулировать правила перевода целых чисел из одной позиционной системы в другую.

D – триггер. Триггер типа D – это устройство с двумя устойчивыми выходами состояниями. Сменой состояния управляют сигналы на информационном входе D, но переключение приходит не сразу, а с приходом тактового импульса на второй вход C. Важнейшее устройство D – триггеров в том что, как только на вход Q устанавливается на тот же уровень напряжения, который в этот момент действует на входе D то есть перебора триггера происходит с некоторым отставанием d + относительно смены сигнала на входе D. [Поэтому D – триггеры еще называют триггеры задержки]!

23. Раскрыть принцип работы асинхронного D-триггера. Привести таблицу состояний. Изобразить условное графическое обозначение.

24. Сформулировать правило перевода правильных дробей из десятичной системы счисления в другие и обратно. Привести примеры применения этого правила.

25. Раскрыть принцип работы асинхронного RS-триггера. Привести таблицу состояний и функциональную схему, изобразить условное графическое обозначение асинхронного RS-триггера с прямыми входами.

RS – триггер.

Триггер типа RS, «запоминает», на какой из двух входов (R или S) поступил последний сигнал: если на вход R, триггер находится в нулевом состоянии (q=0 и q(инверсное)=1, а если на вход S, то в единичном состоянии (q=1 и q(инверсное)=0

26. Сформулировать правило перевода смешанных чисел из десятичной системы счисления в другие и обратно и привести примеры его использования.

БЛа бла бла

27. Раскрыть принцип работы синхронного JK-триггера. Привести таблицу состояний, изобразить условное графическое обозначение, функциональную схему.

JK – триггер.

Триггер типа JK представляет собой устройство с двумя выходными состояниями, обладающими двумя информационными входами J и K. По принципу действия он сходен с RS – триггером, с той разницей, что в состояниях jk – триггера нет неопределенности при одновременном поступлении сигналов высокого уровня на оба входа.

28. Раскрыть механизм составления таблиц сложения и умножения в шестнадцатеричной системе счисления.

Бла. бла.

29. Дать понятие о регистрах и их видах. Рассказать о назначении и устройстве. Изобразить условное графическое обозначение.

30. Дать понятие о формах представления чисел в ЭВМ: с фиксированной запятой и с плавающей запятой.

Аналогично с 30.

31. Дать понятие о дешифраторах, их назначении и видах. Изобразить условное графическое обозначение. Представить таблицу состояний и функциональную схему.

32. Объяснить механизм выполнения арифметических операций над числами в формате с плавающей запятой.

Спросить у Харитончик

33. Дать понятие о мультиплексорах и демультиплексорах. Изобразить условное графическое обозначение.

Де мультиплексор выполняет функцию обратную мультиплексору то есть в соответствии с принятой адресацией Ai направляет информацию с единственного входа D

34. Представить алгоритм получения кода числа в формате с плавающей запятой.

Аналогично с 30.

35. Дать понятие о компараторах.

Аналогично с 30.

36. Дать понятие о булевой алгебре. Раскрыть сущность основных понятий алгебры логики: высказывание, логические константы и переменные, операции и функции.

Ммммм

37. Рассказать о назначении и особенностях работы последовательных регистров. Изобразить условное графическое обозначение и функциональную схему.

В последовательном регистре ввод числа выполняется путем последовательной во времени подачи цифр отдельных Х разрядов. Подача цифр начинается с 0.

38. Назвать и сформулировать законы и тождества алгебры логики.

39. Рассказать о назначении и особенностях работы параллельных регистров. Объяснить принцип работы однофазного и парафазного регистров. Изобразить условное графическое обозначение.

Параллельные регистры.

Пусть на вход регистра поступает пара фазный код числа, при этом для каждого разряда числа предусмотрена (какая то херня) 2 входа на 1 из которых поступает прямой код, а на 2-ой инверсный. Прием такого числа в регистр построенный с использованием простейших синхронных RS – триггеров. Если цифра i-го разряда Ai=1 то поступает 1 на вход S соответствующего триггера при подаче логической 1 на вход С триггер устанавливается в состояние единицы. Если Ai = 0 то поступает единица на вход К и этот триггер устанавливается в состояние 0. Когда на вход триггера поступает однофазный вход числа (без подачи инверсных значений цифр разрядов). Регистр может быть построен с использованием простейших синхронных D триггеров. В таком регистре при подаче (нету хрени) на вход С триггеры устанавливаются в состояние определяемой действующими на входами N цифрами разрядов.

40. Дать понятие о переключательной функции алгебры логики и способах ее описания.

(Спросить)

41. Дать понятие о функционировании регистров сдвига. Привести функциональную схему и объяснить принцип работы.

Суть сдвига заключается в том что цифра сдвигается в i-ом разряде регистра передается в соседний правый разряд.

42. Дать понятие об элементарной конъюнкции, дизъюнкции и канонических формах переключательных функций. Дать определение ранга логической функции, минтерма, макстерма.

Коньюнкция это логическое умножение. А Дизъюнкция это логическая сумма. ------

43. Дать понятие о счетчиках, их видах, назначении. Перечислить и раскрыть сущность основных параметров счетчиков.

Счетчики это – последовательная схема преобразующая на --

Пропорциональной их количеству. Большинство счетчиков снабжены выходом переноса. Для 2-го и 2-го 10 20 справедливы следующие соотношения Q=(D+Sum(c)) CR-(D+sum(c))/M. В этих формулах Q вход для выхода счетчика. D – начальное значение записанное в счетчик, sum(c) – сумма импульсов поступающих на вход С в процессе отсчета. М – модуль счета или число, различают состояний счетчика (число импульсов поступавших на счетный вход после которых счетчик возвращается в исходное состояние). По способам счета триггеры разделяются на:

1 Суммирующие.

2 Вычитающие.

3 Реверсивные – изменяющие направление счета.

44. Сформулировать правило перехода от нормальной (ДНФ) к совершенной (СДНФ) форме переключательной функции аналитическим методом.

Добавление к каждой логической переменной, той же переменной но только инвертированной.

45. Рассказать о современном состоянии и перспективах развития элементной базы и средств вычислительной техники.

(О-О-О ну тут отсебятина походу или инет)

46. Сформулировать правило перехода от нормальной (КНФ) к совершенной (СКНФ) форме переключательной функции аналитическим методом.

Правило состоит в том что к каждой логической переменной добавляется та же логическая переменная но только инвертированная.

47. Дать понятие о назначении и свойствах цифровых автоматов, комбинационных схемах (КС).

48. Раскрыть сущность графического метода перехода от нормальной (ДНФ) к совершенной (СДНФ) форме переключательной функции (с использованием карты Карно).

(тоже просто)

49. Дать понятие о комбинационном сумматоре. Привести условное графическое обозначение, таблицу состояний, схему реализации. Раскрыть особенности работы последовательных и параллельных сумматоров.

50. Дать понятие о минимизации сложных логических функций, заданных в СДНФ и СКНФ методом построения карт Карно.

(тоже просто)

51. Дать понятие о минимизации сложных логических функций, заданных в СДНФ и СКНФ аналитическим методом.

(тоже просто)

52. Дать понятие о полусумматоре. Привести таблицу состояний, функциональную схему, условное графическое обозначение.

Полусумматор - логическая схема, имеющая два входа и два выхода (двухразрядный сумматор, бинарный сумматор). Полусумматор используется для построения двоичных сумматоров. Полусумматор позволяет вычислять сумму A+B, где A и B — это разряды двоичного числа, при этом результатом будут два бита S,C, где S — это бит суммы по модулю, а C — бит переноса. Однако, как можно заметить, для построения схемы двоичного сумматора (трёхразрядный сумматор, тринарный сумматор) необходимо иметь элемент, который суммирует три бита A, B и C, где C — бит переноса из предыдущего разряда, таким элементом является полный двоичный сумматор, который как правило состоит из двух полусумматоров и логического элемента 2ИЛИ.

Троичный полусумматор представляет собой объединение двух троичных бинарных логических функций - «сложение по модулю 3» и «разряд переноса при троичном сложении». Так как существуют две троичных системы счисления - несимметричная, в которой в разряде переноса не бывает значения больше "1" и симметричная (Фибоначчи), в которой в разряде переноса возможны все три состояния трита, и, как минимум, три физических реализации троичных систем - трёхуровневая однопроводная, двухуровневая двухпроводная (BCT) и двухуровневая трёхбитная одноединичная, то и троичных полусумматоров может быть большое множество.

Троичный трёхуровневый полусумматор описан в ^[1].

Троичный двухбитный двухпроводный бинарный (двухоперандный) одноразрядный (BCT) полусумматор, работающий в несимметричной троичной системе счисления, названный двухразрядным сумматором, приведён в ^[2] в разделе BCT Addition в подразделе (f) Circuit diagram и в ^[3] на рис.3.

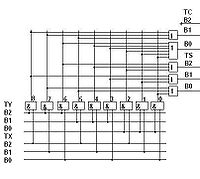
На рисунке справа приведена схема троичного несимметричного полусумматора в трёхбитной одноединичной системе троичных логических элементов

53. Раскрыть механизм минимизации логической функции, заданной СДНФ (СКНФ) методом последовательного исключения переменных.

54. Дать понятие о триггерах, привести классификацию триггеров. Сформулировать основные параметры триггеров.

Триггер (триггерная система) — класс электронных устройств, обладающих способностью длительно находиться в одном из двух устойчивых состояний и чередовать их под воздействием внешних сигналов. Каждое состояние триггера легко распознаётся по значению выходного напряжения. По характеру действия триггеры относятся к импульсным устройствам — их активные элементы (транзисторы, лампы) работают в ключевом режиме, а смена состояний длится очень короткое время.

Динамический триггер представляет собой систему, одно из состояний которой (единичное) характеризуется наличием на выходе непрерывной последовательности импульсов определённой частоты, а другое — отсутствием выходных импульсов (нулевое). Смена состояний производится внешними импульсами (рис. 3). Динамические триггеры в настоящее время используются редко.

К статическим триггерам относят устройства, каждое состояние которых характеризуется неизменными уровнями выходного напряжения (выходными потенциалами): высоким — близким к напряжению питания и низким — около нуля. Статические триггеры по способу представления выходной информации часто называют потенциальными.

Статические (потенциальные) триггеры, в свою очередь, подразделяются на две неравные по практическому значению группы — симметричные и несимметричные триггеры. Оба класса реализуются на двухкаскадном усилителе с положительной обратной связью, а названием своим они обязаны способам организации внутренних электрических связей между элементами схемы.

Симметричные триггеры отличает симметрия схемы и по структуре, и по параметрам элементов обоих плеч. Для несимметричных триггеров характерна неидентичность параметров элементов отдельных каскадов, а также и связей между ними.

Симметричные статические триггеры составляют основную массу триггеров, используемых в современной радиоэлектронной аппаратуре. Схемы симметричных триггеров в простейшей реализации (2х2ИЛИНЕ) показаны на рис. 4.

Асинхронный триггер изменяет своё состояние непосредственно в момент появления соответствующего информационного сигнала(ов), с некоторой задержкой равной сумме задержек на элементах составляющих данный триггер.

Синхронные триггеры реагируют на информационные сигналы только при наличии соответствующего сигнала на так называемом входе синхронизации С (от англ. clock). Этот вход также обозначают термином «такт». Такие информационные сигналы называют синхронными. Синхронные триггеры в свою очередь подразделяют на триггеры со статическим (статические) и динамическим (динамические) управлением по входу синхронизации С.

Одноступенчатые триггеры состоят из одной ступени представляющей собой элемент памяти и схему управления, делятся на триггеры со статическим управлением и триггеры с динамическим управлением.

Триггеры со статическим управлением воспринимают информационные сигналы при подаче на вход С логической единицы (прямой вход) или логического нуля (инверсный вход).

Триггеры с динамическим управлением воспринимают информационные сигналы при изменении (перепаде) сигнала на входе С от 0 к 1 (прямой динамический С-вход) или от 1 к 0 (инверсный динамический С-вход). Также встречается название «триггер управляемый фронтом».

Двухступенчатые триггеры бывают, как правило, со статическим управлением. При одном уровне сигнала на входе С информация, в соответствии с логикой работы триггера, записывается в первую ступень (вторая ступень заблокирована для записи). При другом уровне этого сигнала происходит копирование состояния первой ступени во вторую (первая ступень заблокирована для записи), выходной сигнал появляется в этот момент времени с задержкой равной задержке срабатывания ступени. Обычно двухступенчатые триггеры применяются в схемах, где логические функции входов триггера зависят от его выходов, во избежание временны́х гонок. Двухступенчатые триггеры с динамическим управлением встречаются крайне редко. Двухступенчатый триггер обозначают ТТ.

Триггеры со сложной логикой бывают также одно- и двухступенчатые. В этих триггерах наряду с синхронными сигналами присутствуют и асинхронные. Такой триггер изображён на рис. 1, верхний (S) и нижний (R) входные сигналы являются асинхронными.

Триггерные схемы классифицируют также по следующим признакам:

55. Дать понятие о сумматоре. Раскрыть особенности последовательных и параллельных сумматоров. Привести таблицу состояний и функциональную схему.

56. Дать понятие о минимизации исходной логической функции, заданной в СДНФ (СКНФ). Перечислить методы минимизации.

реобразование логических функций с целью упрощения

их аналитического представления называются минимизацией.

Существуют два направления минимизации:

1. Кратчайшая форма записи (цель – минимизировать ранг каждого терма). При

этом получаются кратчайшие формы КДНФ, ККНФ, КПНФ.

2. Получение минимальной формы записи (цель – получение минимального числа

символов для записи всей функции сразу).

При этом следует учесть, что ни один из способов минимизации не универсален!

Существуют различные методы минимизации:

1. Метод непосредственных преобразований логических функций. (1.1)

При применении данного метода:

а) Записываются ДСНФ логических функций

б) Форма преобразуется и упрощается с использованием аксиом алгебры логики.

При этом, в частности, выявляются в исходном ДСНФ так называемые соседние

min-термы, в которых есть по одной не совпадающей переменной.

Графический и аналитический.

57. Дать понятие о функционально полных системах (базисах). Рассказать о логических базисах, используемых в теории синтеза комбинационных схем.

58. Раскрыть механизм перехода от нормальной (КНФ) к совершенной (СКНФ) форме переключательной функции графическим методом (с использованием карты Карно).

59. Раскрыть сущность метода Квайна для минимизации логической функции.

способ представления функции в ДНФ или КНФ с минимальным количеством членов и минимальным набором переменных.^[1][2][3]
Преобразование функции можно разделить на два этапа:

· а первом этапе осуществляется переход от канонической формы (СДНФ или СКНФ) к так называемой сокращённой форме;

· на втором этапе — переход от сокращённой формы к минимальной форме.

Первый этап (получение сокращённой формы)

Второй этап(табличный) (получение минимальной формы)

60. Сформулировать алгоритм синтеза комбинационной схемы по заданной таблице значений.

Дата добавления: 2015-08-17