
Читайте также:
|
Нормативные и расчетные значения характеристик грунта вычисляют для каждого выделенного на площадке строительства инженерно-геологического элемента (слоя грунта). За нормативное значение характеристики принимают среднее арифметическое значение результатов частных определений. При переходе к расчетному значению учитывается, что среднее значение вследствие неоднородности грунта и ограниченного числа определений может содержать ошибку, которая должна быть исключена. Расчетные значения устанавливают для характеристик, используемых в расчетах оснований и фундаментов.
Статистическую обработку опытных данных начинают с проверки на исключение возможных грубых ошибок (отскоков). Исключать необходимо максимальное или минимальное значение Хi для которого выполняется условие
 ,
,
 (1.8)
(1.8)

где  — среднее значение; v — статистический критерий, принимаемый по табл. 1.21; Sdis — смещенная оценка среднего квадратического отклонения:
— среднее значение; v — статистический критерий, принимаемый по табл. 1.21; Sdis — смещенная оценка среднего квадратического отклонения:
 ,
,
 (1.9)
(1.9)

здесь n — количество определений.
ТАБЛИЦА 1.21. ЗНАЧЕНИЯ СТАТИСТИЧЕСКОГО КРИТЕРИЯ
| Число определений | v | Число определений | v | Число определений | v | ||
| 2,07 | 2,56 | 2,78 | |||||
| 2,18 | 2,60 | 2,88 | |||||
| 2,27 | 2,64 | 2,96 | |||||
| 2,35 | 2,67 | 3,02 | |||||
| 2,41 | 2,70 | 3,07 | |||||
| 2,47 | 2,73 | 3,12 | |||||
| 2,52 | 2,75 | 3,16 |
Далее вычисляют:
– нормативное (среднее арифметическое) значение
 ;
;
 (1.10)
(1.10)

– среднее квадратическое отклонение
 ;
;
 (1.11)
(1.11)

– коэффициент вариации
V = S / Xn;
 (1.12)
(1.12)

– ошибку среднего значения  (в абсолютных единицах) или
(в абсолютных единицах) или  (относительная ошибка)
(относительная ошибка)
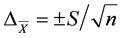 ;
; 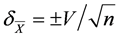 ;
;
 (1.13)
(1.13)

– доверительный интервал, характеризующий область вокруг среднего значения, в пределах которой с заданной вероятностью α находится "истинное" (генеральное) среднее значение,
 ;
;  ;
;
 (1.14)
(1.14)

где t α — коэффициент, принимаемый по табл. 1.22 в зависимости от заданной вероятности (надежности) α и числа определений n;
ТАБЛИЦА 1.22. ЗНАЧЕНИЯ КОЭФФИЦИЕНТА t α ПРИ ОДНОСТОРОННЕЙ ДОВЕРИТЕЛЬНОЙ ВЕРОЯТНОСТИ α
| Число определений n –1 или n –2 | t α при α | Число определений n –1 или n –2 | t α при α | ||
| 0,85 | 0,95 | 0,85 | 0,95 | ||
| 1,34 | 2,92 | 1,08 | 1,77 | ||
| 1,26 | 2,35 | 1,08 | 1,76 | ||
| 1,19 | 2,13 | 1,07 | 1,75 | ||
| 1,16 | 2,01 | 1,07 | 1,76 | ||
| 1,13 | 1,94 | 1,07 | 1,74 | ||
| 1,12 | 1,90 | 1,07 | 1,73 | ||
| 1,11 | 1,86 | 1,07 | 1,73 | ||
| 1,10 | 1,83 | 1,06 | 1,72 | ||
| 1,10 | 1,81 | 1,05 | 1,70 | ||
| 1,09 | 1,80 | 1,06 | 1,68 | ||
| 1,08 | 1,78 | 1,05 | 1,67 |
– коэффициент надежности по грунту
γg = 1/(1 ± δ);
 (1.15)
(1.15)

– расчетное значение характеристик
X = Xn / γg
 (1.16)
(1.16)

или
X = Xn ± Δ; X = Xn (1 ± δ).
 (1.17)
(1.17)

Указанная статистическая обработка применяется для таких характеристик грунтов, используемых при расчетах оснований, как плотность и модуль деформации нескальных грунтов и предел прочности на одноосное сжатие скальных грунтов. Для физических характеристик вычисляются их нормативные значения. Для модуля деформации, а также характеристик относительной просадочности и набухания допускается принимать расчетные значения равными нормативным.
Для прочностных характеристик грунтов — угла внутреннего трения φ и удельного сцепления с — методика статистической обработки имеет следующие особенности. Нормативные значения φ и с определяют по нормативной зависимости τ = σ tgφ + c, вычисляемой методом наименьших квадратов на основе всех определений τ в рассматриваемом слое грунта. Вычисления проводят по формулам:
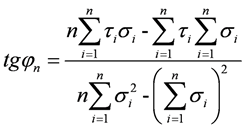 ;
;
 (1.18)
(1.18)
 ,
,
 (1.19)
(1.19)
или
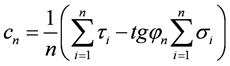 .
.
 (1.20)
(1.20)

Средние квадратические ошибки с и φ определяются по формулам:
 ;
;
 (1.21)
(1.21)
 ,
,
 (1.22)
(1.22)
где
 .
.
 (1.23)
(1.23)

Коэффициенты вариации φ и с вычисляются по формуле (1.12), а доверительный интервал
δtgφ = t α Vtgφ; δc = t α Vc.
 (1.24)
(1.24)

Расчетные значения φ и с находят по формулам (1.16) и (1.17). Доверительная вероятность α принимается равной 0,85 при расчетах оснований по деформациям и равной 0,95 при расчетах несущей способности оснований и расчетах подпорных стен.
Расчетные значения характеристик грунта φ, с и ρ для расчетов оснований по несущей способности обозначаются φI, сI и ρ I, а для расчетов по деформациям — φII, сII и ρ II.
Пример 1.1. Для известняков определено 13 значений предела прочности на одноосное сжатие в водонасыщенном состоянии Rci (табл. 1.23). Делаем проверку на исключение возможные грубых ошибок, для чего вычисляем:
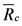 = 222/13 = 17,08 ≈ 17 МПа;
= 222/13 = 17,08 ≈ 17 МПа;
Sdis =  = 5,14 ≈ 5 МПа.
= 5,14 ≈ 5 МПа.
ТАБЛИЦА 1.23. К ПРИМЕРУ 1.1
| Номер опыта | Rci, МПа | 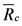 – Rci – Rci
| (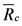 – Rci)2 – Rci)2
|
| –1 | |||
| –5 | |||
| –7 | |||
| –3 | |||
| –1 | |||
| –10 | |||
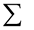
| – |
По табл. 1.21 находим для n = 13, v = 2,56, тогда vSdis = 13. Наибольшее отклонение от среднего значения составляет 10 (опыт № 11), что меньше 13, следовательно, опытные данные не содержат грубых ошибок. Для вычисления расчетного значения Rc находим:
S =  = 5,35 ≈ 5 МПа; V = 5/17 = 0,29.
= 5,35 ≈ 5 МПа; V = 5/17 = 0,29.
Поскольку прочность скальных грунтов используется для оценки несущей способности оснований из этих грунтов, расчетное значение Rс должно быть определено с доверительной вероятностью 0,95. Для α = 0,95 и n -1 = 12 по табл. 1.22 находим t α = 1,78.
Тогда по формуле (1.14)
δ = 1,78 · 0,29/  = 0,14.
= 0,14.
Далее воспользуемся формулой (1.17): Rс = 17 (1 – 0,14) = 14,62 ≈ 15 МПа.
Здесь значение δ взято со знаком минус, так как это обеспечит большую надежность расчета оснований по несущей способности.
Пример 1.2. Для инженерно-геологического элемента, сложенного суглинками, было выполнено 27 лабораторных определений сопротивления срезу τ в девяти сериях при трех значениях нормального давления σ = 100, 200 и 300 кПа (табл. 1,24).
Прежде чем приступить к вычислению нормативных и расчетных значений с и φ, следует выполнить проверку на исключение грубых ошибок в определениях τ при каждом значении нормального давления. Необходимые для этого подсчеты приведены в табл. 1.24. Значения статистического критерия v приняты по табл. 1.21 для n = 9. В результате проверки получено, что при всех значениях нормального давления  , следовательно, опытные данные не содержат грубых ошибок.
, следовательно, опытные данные не содержат грубых ошибок.
Вычисления нормативных и расчетных значений с и φ следует вести в табличной форме (табл. 1.25).
ТАБЛИЦА 1.24. К ПРИМЕРУ 1.2
| Номер серии опытов | σ = 100 кПа | σ = 200 кПа | σ = 300 кПа | ||||||
| τi, кПа | 
| ( )2 )2
| τi, кПа | 
| ( )2 )2
| τi, кПа | 
| ( )2 )2
| |
| –3,33 | 11,0888 | 12,22 | 149,3284 | 22,22 | 493,7284 | ||||
| 1,67 | 2,7889 | 7,22 | 52,1284 | 17,22 | 296,5284 | ||||
| -3,33 | 11,0889 | –12,78 | 163,3284 | –22,78 | 518,9284 | ||||
| 6,67 | 44,4889 | –2,78 | 7,7284 | –12,78 | 163,3284 | ||||
| –8,33 | 69,3889 | –2,78 | 7,7284 | 2,22 | 4,9284 | ||||
| 6,67 | 44,4889 | 17,22 | 296,5284 | 2,22 | 4,9284 | ||||
| –13,33 | 177,6889 | –12,78 | 163,3284 | –12,78 | 163,3284 | ||||
| 11,07 | 136,1889 | 7,22 | 52,1284 | 2,22 | 4,9284 | ||||
| 1,67 | 2,7889 | –12,78 | 163,3284 | 2,22 | 4,9284 | ||||
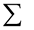
| — | 500,0001 | — | 1055,5556 | — | 1656,5556 | |||
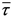 1 = 645/9 = 71,67; Sdis = 1 = 645/9 = 71,67; Sdis =  = 7,45; v = 2,35; vSdis = 17,51; 13,33 < 17,51 = 7,45; v = 2,35; vSdis = 17,51; 13,33 < 17,51
| 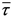 2 = 965/9 = 107,22; Sdis = 2 = 965/9 = 107,22; Sdis = 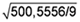 = 10,83; v = 2,35; vSdis = 25,45; 17,22 < 25,45 = 10,83; v = 2,35; vSdis = 25,45; 17,22 < 25,45
| 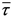 3 = 1235/9 = 137,22; Sdis = 3 = 1235/9 = 137,22; Sdis =  = 13,56; v = 2,35; vSdis = 31,87; 22,78 < 31,87 = 13,56; v = 2,35; vSdis = 31,87; 22,78 < 31,87
|
ТАБЛИЦА 1.25. К ПРИМЕРУ 1.2
| Номер опыта | σ i | τi | σ2 i | σ i τi | 
| 
| ( )2 )2
|
| 10 000 | 7 500 | 72,59 | –2,41 | 5,8081 | |||
| 10 000 | 7 000 | 72,59 | 2,59 | 6,7081 | |||
| 10 000 | 7 500 | 72,59 | –2,41 | 5,8081 | |||
| 10 000 | 6 500 | 72,59 | 7,59 | 57,6081 | |||
| 10 000 | 8 000 | 72,59 | –7,41 | 54,9081 | |||
| 10 000 | 6 500 | 72,59 | 7,59 | 57,6081 | |||
| 10 000 | 8 500 | 72,59 | –12,41 | 164,0081 | |||
| 10 000 | 6 000 | 72,59 | 12,59 | 158,5081 | |||
| 10 000 | 7 000 | 72,59 | 2,59 | 6,7081 | |||
| 40 000 | 19 000 | 105,37 | 10,37 | 107,5369 | |||
| 40 000 | 20 000 | 105,37 | 5,37 | 28,8369 | |||
| 40 000 | 24 000 | 105,37 | –14,63 | 214,0369 | |||
| 40 000 | 22 000 | 105,37 | –4,63 | 21,4369 | |||
| 40 000 | 22 000 | 105,37 | –4,63 | 21,4369 | |||
| 40 000 | 18 000 | 105,37 | 15,37 | 236,2369 | |||
| 40 000 | 24 000 | 105,37 | –14,63 | 214,0369 | |||
| 40 000 | 20 000 | 105,37 | 5,37 | 28,8369 | |||
| 40 000 | 24 000 | 105,37 | –14,63 | 214,0369 | |||
| 90 000 | 34 500 | 138,15 | 23,15 | 535,9226 | |||
| 90 000 | 36 000 | 138,15 | 18,15 | 329,4225 | |||
| 90 000 | 48 000 | 138,15 | –21,85 | 477,4225 | |||
| 90 000 | 45 000 | 138,15 | –11,85 | 140,4225 | |||
| 90 000 | 40 500 | 138,15 | 3,15 | 9,9225 | |||
| 90 000 | 40 500 | 138,15 | 3,15 | 9,9225 | |||
| 90 000 | 45 000 | 138,15 | –11,85 | 140,4225 | |||
| 90 000 | 40 500 | 138,15 | 3,15 | 9,9225 | |||
| 90 000 | 40 500 | 138,15 | 3,15 | 9,9225 | |||
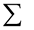
| 1 260 000 | 628 000 | – | – | 3257,4075 |
В графы 2 и 3 вписываем экспериментальные значения σ i и τ i. После вычислений, внесенных в графы 4 и 5, определяем tg φn и сn. Значения в графе 6 получаем путем подстановки найденных значений tg φn и сn в уравнение  .
.
Обозначим знаменатель в формулах (1.18), (1,19), (1,21) и (1.22) буквой М и вычислим его значение:
М = 27 · 1 260 000 – 5 4002 = 4 860 000;
tg φn =  (27 · 628 000 – 2845 · 5400) = 0,3278;
(27 · 628 000 – 2845 · 5400) = 0,3278;
φn = 18°10´ ≈ 18°;
cn =  (2645 · 1 260 000 – 5400 · 628 000) =39,81 кПа.
(2645 · 1 260 000 – 5400 · 628 000) =39,81 кПа.
После заполнении граф 7 и 8 находим:
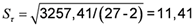 кПа;
кПа;
 кПа;
кПа;
 ;
;
Vc = 5,81/39,81 = 0,15; Vtgφ = 0,0269/0,3278 = 0,08.
Определяем расчетные значения с и φ для расчетов основания по первому предельному состоянию. Для α = 0,95 и n – 2 = 25, t α = 1,71. Тогда:
δ c = 1,71 · 0,15 = 0,26; γg (с) = 1/(1 – 0,26) = 1,35;
δ tgφ = 1,71 · 0,08 = 0,14; γg (tgφ) = 1/(1 – 0,14) = 1,16;
cI = 39,81/1,35 = 29,49 ≈ 29 кПа; tgφI = 0,3278/1,16 = 0,28; φI = 15°33' ≈ 61°.
Дата добавления: 2015-08-17; просмотров: 189 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ФИЛЬТРАЦИОННЫЕ СВОЙСТВА ГРУНТОВ | | | ОБЩИЕ СВЕДЕНИЯ |