В геометрии

Объём - количественная характеристика пространственного тела. За единицу измерения объёма принимают куб с ребром 1мм(1ди, 1м и т.д.).

Количество кубов единичного объёма размещенных в данном теле - объём тела.

Аксиомы объёма:

Объём - это неотрицательная величина.

Объём тела равен сумме объёмов тел, его составляющих.

Найдем формулу для вычисления объёма (рис. 10):

выберем ось ОХ по направлению расположения этого тела;

определим границы расположения тела относительно ОХ;

введем вспомогательную функцию S(x) задающую следующее соответствие: каждому x из отрезка [a;b] поставим в соответствие площадь сечения данной фигуры плоскостью, проходящей через заданную точку x перпендикулярно оси ОХ.

разобьем отрезок [a;b] на n равных частей и через каждую точку разбиения проведём плоскость перпендикулярную оси ОХ, при этом наше тело разобьется на части. По аксиоме

V=V1+V2+...+Vn=lim(S(x1)Dx +S(x2)Dx+...+S(xn)Dx

n®¥

Dx®0, а Sk®Sk+1, а объем части, заключенной между двумя соседними плоскостями равна объему цилиндра Vц=SоснH.

Рис. 10

Имеем сумму произведений значений функций в точках разбиения на шаг разбиения, т.е. интегральную сумму. По определению определенного интеграла, предел этой суммы при n®¥ называется интегралом a

ò S(x)dx

b

a

V= ò S(x)dx, где S(x) – сечение плоскости, проходящей через

b выбранную точку перпендикулярно оси ОХ.

Для нахождения объема надо:

1). Выбрать удобным способом ось ОХ.

2). Определить границы расположения этого тела относительно оси.

3). Построить сечение данного тела плоскостью перпендикулярно оси ОХ и проходящей через соответственную точку.

4). Выразить через известные величины функцию, выражающую площадь данного сечения.

5). Составить интеграл.

6). Вычислив интеграл, найти объем.

Объем фигур вращения

Тело, полученное в результате вращения плоской фигуры, относительно какой-то оси, называют фигурой вращения.

Функция S(x) у фигуры вращения есть круг.

Sсеч = pr2

Sсеч(x)=p f 2(x)

b

V= ò f 2(x)

a

Длина дуги плоской кривой

Пусть на отрезке [a;b] функция y = f(x) имеет непрерывную производную y’ = f ’(x). В этом случае длину дуги l “куска” графика функции y = f(x), xÎ[a;b] можно найти по формуле

b

l = ò Ö(1+f’(x)2)dx

a

Геометрические приложения двойных интегралов

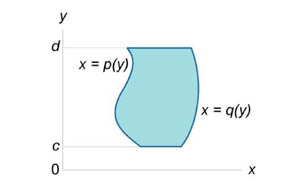
Площадь плоской фигуры Если f (x,y) = 1 в интеграле , то двойной интеграл равен площади области интегрирования R. Площадь области типа I (элементарной относительно оси О y) (рисунок 1) выражается через повторный интеграл в виде Аналогично, площадь области типа II (элементарной относительно оси О x) (рисунок 2) описывается формулой

Рис.1		Рис.2

Объем тела Если f (x,y) > 0 в области интегрирования R, то объем цилиндрического тела с основанием R, ограниченного сверху поверхностью z = f (x,y), выражается формулой В случае, когда R является областью типа I, ограниченной линиями , объем тела равен Для области R типа II, ограниченной графиками функций , объем соответственно равен Если в области R выполняется неравенство , то объем цилиндрического тела между поверхностями z ₁ = f (x,y) и z ₂ = g (x,y) с основанием R равен Площадь поверхности Предположим, что поверхность задана функцией z = f (x,y), имеющей область определения R. Тогда площадь такой поверхности над областью z определяется формулой при условии, что частные производные и непрерывны всюду в области R. Площадь и объем в полярных координатах Пусть S является областью, ограниченной линиями (рисунок 3). Тогда площадь этой области определяется формулой

Рис.3

Объем тела, ограниченного сверху поверхностью 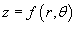с основанием S, выражается в полярных координатах в виде

Интегрирование тригонометрических функций

Интегралы вида

вычисляют, используя следующие тригонометрические формулы:

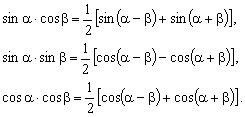
Пример Найти площадь области R, ограниченной гиперболами и вертикальными прямыми .

Найти объем тела в первом октанте, ограниченного плоскостями .

Вычислить объем тела, ограниченного поверхностями .

Найти площадь лепестка розы, заданной уравнением .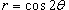

Вычислить объем единичного шара

Геометрические приложения криволинейных интегралов

Криволинейные интегралы имеют многочисленные приложения в математике, физике и прикладных расчетах. В частности, с их помощью вычисляются

• Длина кривой;
• Площадь области, ограниченной замкнутой кривой;
• Объем тела, образованного вращением замкнутой кривой относительно некоторой оси.

Длина кривой Пусть C является гладкой, кусочно-непрерывной кривой, которая описывается вектором . Длина данной кривой выражается следующим криволинейным интегралом где − производная, а − компоненты векторной функции . Если кривая C задана в плоскости, то ее длина выражается формулой 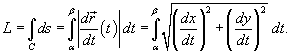Если кривая C представляет собой график заданной явно, непрерывной и дифференцируемой функции в плоскости O xy, то длина такой кривой вычисляется по формуле 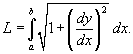Наконец, если кривая C задана в полярных координатах уравнением , и функция 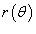является непрерывной и дифференцируемой в интервале 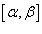, то длина кривой определяется выражением 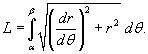Площадь области, ограниченной замкнутой кривой Пусть C является гладкой, кусочно-непрерывной и замкнутой кривой, заданной в плоскости O xy (рисунок 1). Тогда площадь области R, ограниченной данной кривой, определяется формулами Здесь предполагается, что обход кривой C производится против часовой стрелки. Если замкнутая кривая C задана в параметрическом виде , то площадь соответствующей области равна

Рис.1		Рис.2

Объем тела, образованного вращением замкнутой кривой относительно оси Ox Предположим, что область R расположена в верхней полуплоскости y ≥ 0 и ограничена гладкой, кусочно-непрерывной и замкнутой кривой C, обход которой осуществляется против часовой стрелки. В результате вращения области R вокруг оси O x образуется тело Ω (рисунок 2). Объем данного тела определяется формулами

Рассмотрим пример. Найти .

Решение. - это несобственный интеграл, и прежде всего следует установить его сходимость. По определению, . Первый из интегралов – собственный, второй – сходится по 1-й теореме о сравнении, т.к. при справедливы неравенств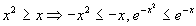а , а , очевидно, сходится.

Обозначим (очевидно, 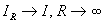). Тогда, поскольку обозначение переменной интегрирования можно выбрать произвольным, , где - квадрат, а - четверти круга, соответственно, радиусов . Т.к. , то по свойствам 2 и 3 двойного интеграла . В интеграле п перейдем к полярным координатам: . Аналогично, и 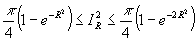. При стремлении получаем, что , т.е. .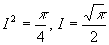

Найти длину кривой при условии .

Вычислить длину астроиды .

Найти длину циклоиды, заданной в параметрическом виде вектором 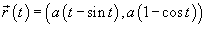в интервале

Вычислить длину параболы в интервале .

Найти длину кардиоиды, заданной в полярных координатах уравнением

Найти площадь области, ограниченной гиперболой , осью O x и вертикальными прямыми x = 1, x = 2

Дата добавления: 2015-08-17