Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АрхитектураБиологияГеографияДругоеИностранные языки
ИнформатикаИсторияКультураЛитератураМатематика
МедицинаМеханикаОбразованиеОхрана трудаПедагогика
ПолитикаПравоПрограммированиеПсихологияРелигия
СоциологияСпортСтроительствоФизикаФилософия
ФинансыХимияЭкологияЭкономикаЭлектроника

Угол между плоскостями. Условия параллельности и перпендикулярности плоскостей.

Читайте также:
  1. D. Ратификация международных соглашений
  2. F) Между встречным и первоначальным исками имеется взаимная связь.
  3. G. ТРАНСГРАНИЧНОЕ УПРАВЛЕНИЕ - Международное сотрудничество; 1 млн. долл. США; 2-10 лет
  4. Gastroenterostomia retrocolica posterior (операция Гаккера в модификации Петерсена). Наложение швов-держалок между желудком и тонкой кишкой.
  5. I. Адаптация системы представительной демократии к японским условиям
  6. I. Международно-правовые акты
  7. I. Тест по Международному частному праву для специальностей юридического профиля.

сли заданы уравнения плоскостей A1

x + B1y + C1z + D1 = 0 и A2x + B2y + C2z + D2 = 0, то угол между плоскостями можно найти, используя следующую формулу

 

cos α   = |A1·A2 + B1·B2 + C1·C2|
(A12 + B12 + C12)1/2(A22 + B22 + C22)1/2
   

На основе полученной выше формулы для нахождения угла между плоскостями можно найти условия параллельности и перпендикулярности плоскостей.

 

Для того, чтобы плоскости были перпендикулярны необходимо и достаточно, чтобы косинус угла между плоскостями равнялся нулю. Это условие выполняется, если:

.

 

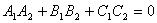Плоскости параллельны, векторы нормалей коллинеарны: ïï .Это условие выполняется, если: .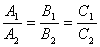

 

Дата добавления: 2015-08-17; просмотров: 41 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
Нормальное уравнение плоскости. Нормирующий множитель. Применение нормального уравнения плоскости| Витрина с объёмной выкладкой.
mybiblioteka.su - 2015-2024 год. (0.007 сек.)